Fleet Size and Mix Split-Delivery Vehicle Routing
Paper and Code
Dec 06, 2016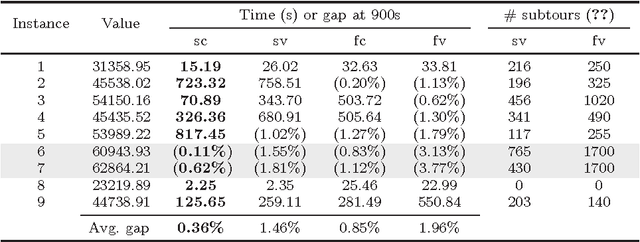

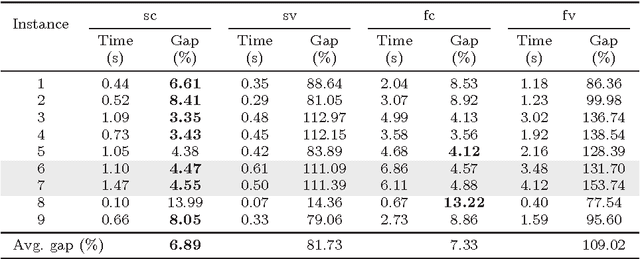
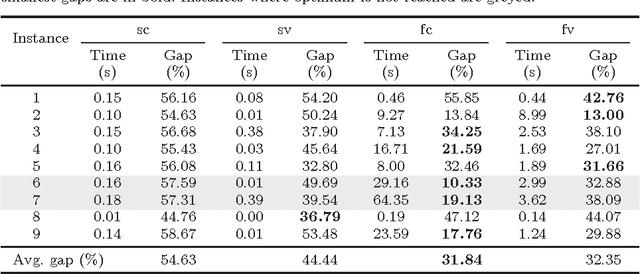
In the classic Vehicle Routing Problem (VRP) a fleet of of vehicles has to visit a set of customers while minimising the operations' costs. We study a rich variant of the VRP featuring split deliveries, an heterogeneous fleet, and vehicle-commodity incompatibility constraints. Our goal is twofold: define the cheapest routing and the most adequate fleet. To do so, we split the problem into two interdependent components: a fleet design component and a routing component. First, we define two Mixed Integer Programming (MIP) formulations for each component. Then we discuss several improvements in the form of valid cuts and symmetry breaking constraints. The main contribution of this paper is a comparison of the four resulting models for this Rich VRP. We highlight their strengths and weaknesses with extensive experiments. Finally, we explore a lightweight integration with Constraint Programming (CP). We use a fast CP model which gives good solutions and use the solution to warm-start our models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge