Sebastian Will
Runtime Analyses of Multi-Objective Evolutionary Algorithms in the Presence of Noise
May 22, 2023Abstract:In single-objective optimization, it is well known that evolutionary algorithms also without further adjustments can tolerate a certain amount of noise in the evaluation of the objective function. In contrast, this question is not at all understood for multi-objective optimization. In this work, we conduct the first mathematical runtime analysis of a simple multi-objective evolutionary algorithm (MOEA) on a classic benchmark in the presence of noise in the objective functions. We prove that when bit-wise prior noise with rate $p \le \alpha/n$, $\alpha$ a suitable constant, is present, the \emph{simple evolutionary multi-objective optimizer} (SEMO) without any adjustments to cope with noise finds the Pareto front of the OneMinMax benchmark in time $O(n^2\log n)$, just as in the case without noise. Given that the problem here is to arrive at a population consisting of $n+1$ individuals witnessing the Pareto front, this is a surprisingly strong robustness to noise (comparably simple evolutionary algorithms cannot optimize the single-objective OneMax problem in polynomial time when $p = \omega(\log(n)/n)$). Our proofs suggest that the strong robustness of the MOEA stems from its implicit diversity mechanism designed to enable it to compute a population covering the whole Pareto front. Interestingly this result only holds when the objective value of a solution is determined only once and the algorithm from that point on works with this, possibly noisy, objective value. We prove that when all solutions are reevaluated in each iteration, then any noise rate $p = \omega(\log(n)/n^2)$ leads to a super-polynomial runtime. This is very different from single-objective optimization, where it is generally preferred to reevaluate solutions whenever their fitness is important and where examples are known such that not reevaluating solutions can lead to catastrophic performance losses.
Decomposition During Search for Propagation-Based Constraint Solvers
Jun 11, 2008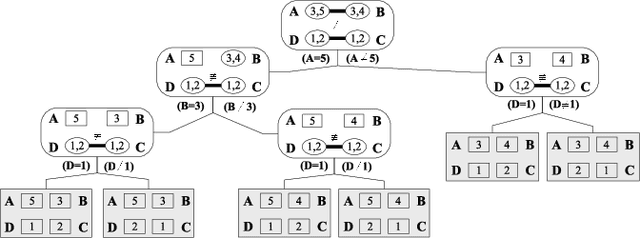
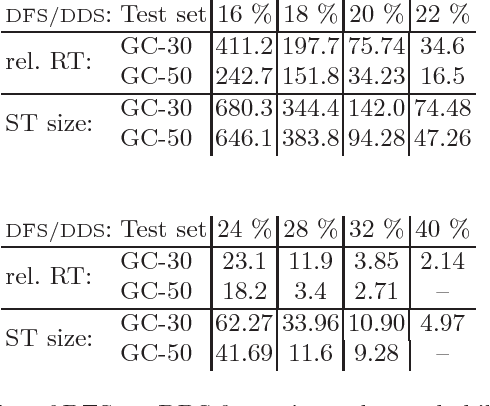
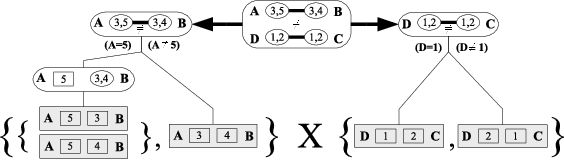

Abstract:We describe decomposition during search (DDS), an integration of And/Or tree search into propagation-based constraint solvers. The presented search algorithm dynamically decomposes sub-problems of a constraint satisfaction problem into independent partial problems, avoiding redundant work. The paper discusses how DDS interacts with key features that make propagation-based solvers successful: constraint propagation, especially for global constraints, and dynamic search heuristics. We have implemented DDS for the Gecode constraint programming library. Two applications, solution counting in graph coloring and protein structure prediction, exemplify the benefits of DDS in practice.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge