Geoffrey J. McLachlan
Some Simulation and Empirical Results for Semi-Supervised Learning of the Bayes Rule of Allocation
Oct 25, 2022Abstract:There has been increasing attention to semi-supervised learning (SSL) approaches in machine learning to forming a classifier in situations where the training data consists of some feature vectors that have their class labels missing. In this study, we consider the generative model approach proposed by Ahfock&McLachlan(2020) who introduced a framework with a missingness mechanism for the missing labels of the unclassified features. In the case of two multivariate normal classes with a common covariance matrix, they showed that the error rate of the estimated Bayes' rule formed by this SSL approach can actually have lower error rate than the one that could be formed from a completely classified sample. In this study we consider this rather surprising result in cases where there may be more than two normal classes with not necessarily common covariance matrices.
Functional Mixtures-of-Experts
Feb 04, 2022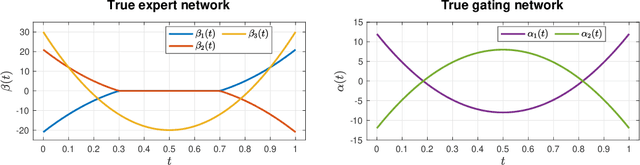
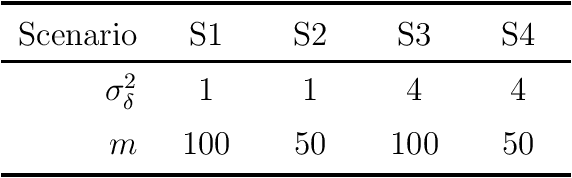
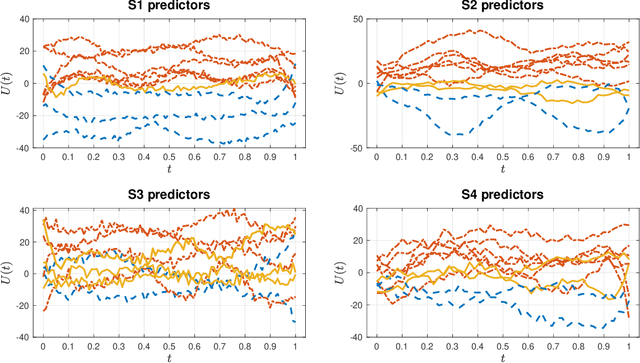
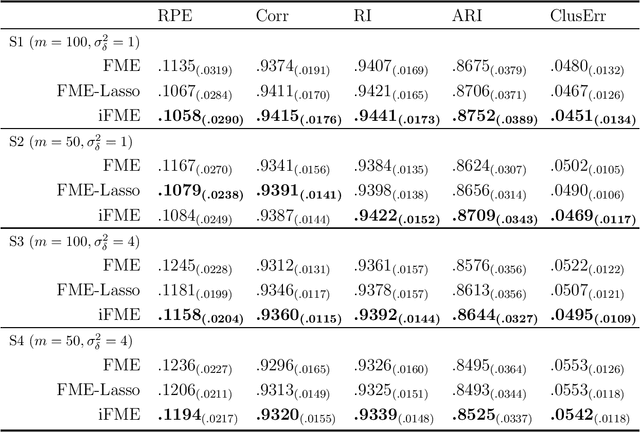
Abstract:We consider the statistical analysis of heterogeneous data for clustering and prediction purposes, in situations where the observations include functions, typically time series. We extend the modeling with Mixtures-of-Experts (ME), as a framework of choice in modeling heterogeneity in data for prediction and clustering with vectorial observations, to this functional data analysis context. We first present a new family of functional ME (FME) models, in which the predictors are potentially noisy observations, from entire functions, and the data generating process of the pair predictor and the real response, is governed by a hidden discrete variable representing an unknown partition, leading to complex situations to which the standard ME framework is not adapted. Second, we provide sparse and interpretable functional representations of the FME models, thanks to Lasso-like regularizations, notably on the derivatives of the underlying functional parameters of the model, projected onto a set of continuous basis functions. We develop dedicated expectation--maximization algorithms for Lasso-like regularized maximum-likelihood parameter estimation strategies, to encourage sparse and interpretable solutions. The proposed FME models and the developed EM-Lasso algorithms are studied in simulated scenarios and in applications to two real data sets, and the obtained results demonstrate their performance in accurately capturing complex nonlinear relationships between the response and the functional predictor, and in clustering.
Semi-Supervised Learning of Classifiers from a Statistical Perspective: A Brief Review
Apr 13, 2021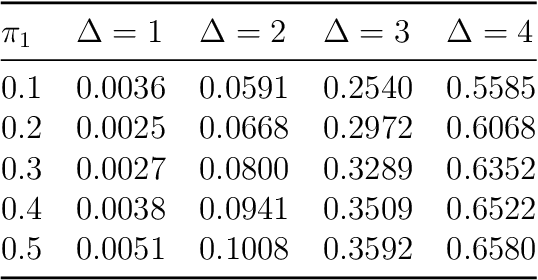
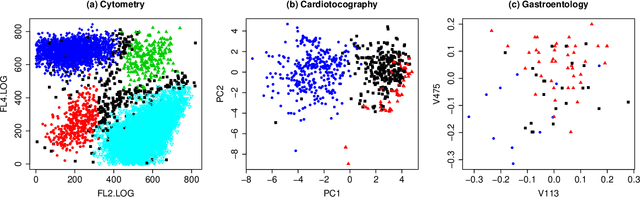
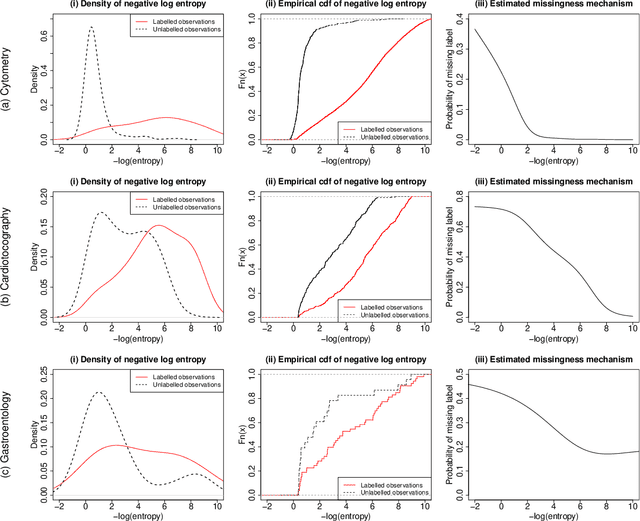
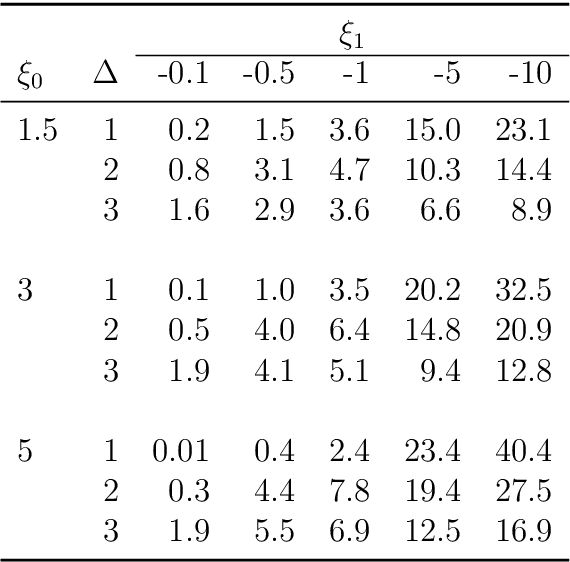
Abstract:There has been increasing attention to semi-supervised learning (SSL) approaches in machine learning to forming a classifier in situations where the training data for a classifier consists of a limited number of classified observations but a much larger number of unclassified observations. This is because the procurement of classified data can be quite costly due to high acquisition costs and subsequent financial, time, and ethical issues that can arise in attempts to provide the true class labels for the unclassified data that have been acquired. We provide here a review of statistical SSL approaches to this problem, focussing on the recent result that a classifier formed from a partially classified sample can actually have smaller expected error rate than that if the sample were completely classified.
Harmless label noise and informative soft-labels in supervised classification
Apr 07, 2021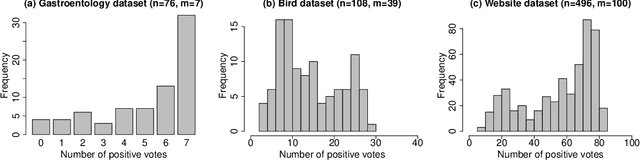
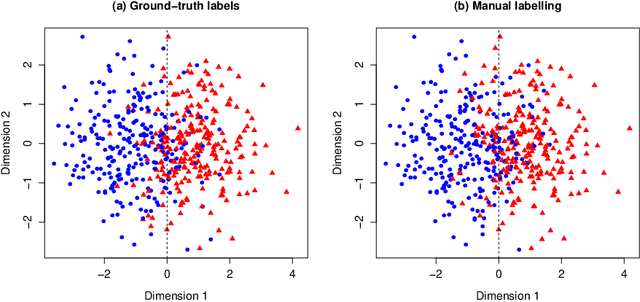

Abstract:Manual labelling of training examples is common practice in supervised learning. When the labelling task is of non-trivial difficulty, the supplied labels may not be equal to the ground-truth labels, and label noise is introduced into the training dataset. If the manual annotation is carried out by multiple experts, the same training example can be given different class assignments by different experts, which is indicative of label noise. In the framework of model-based classification, a simple, but key observation is that when the manual labels are sampled using the posterior probabilities of class membership, the noisy labels are as valuable as the ground-truth labels in terms of statistical information. A relaxation of this process is a random effects model for imperfect labelling by a group that uses approximate posterior probabilities of class membership. The relative efficiency of logistic regression using the noisy labels compared to logistic regression using the ground-truth labels can then be derived. The main finding is that logistic regression can be robust to label noise when label noise and classification difficulty are positively correlated. In particular, when classification difficulty is the only source of label errors, multiple sets of noisy labels can supply more information for the estimation of a classification rule compared to the single set of ground-truth labels.
Estimation of Classification Rules from Partially Classified Data
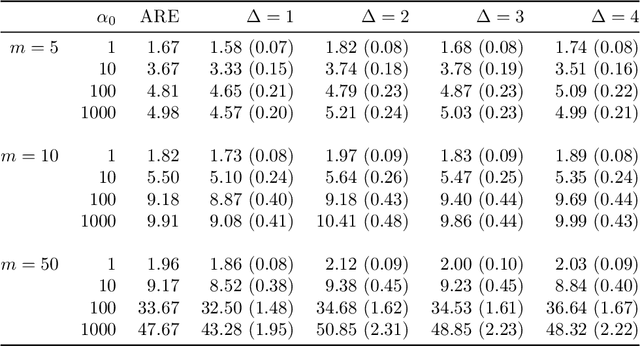
Apr 13, 2020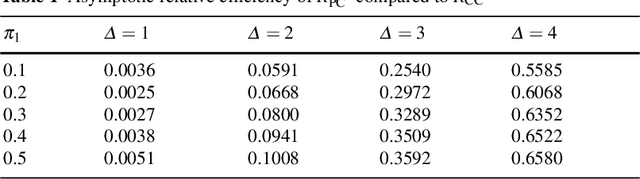
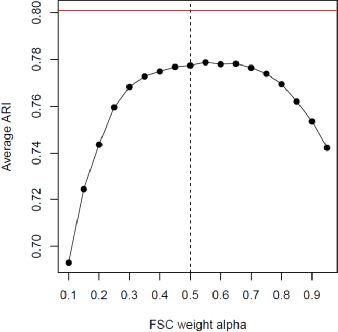
Abstract:We consider the situation where the observed sample contains some observations whose class of origin is known (that is, they are classified with respect to the g underlying classes of interest), and where the remaining observations in the sample are unclassified (that is, their class labels are unknown). For class-conditional distributions taken to be known up to a vector of unknown parameters, the aim is to estimate the Bayes' rule of allocation for the allocation of subsequent unclassified observations. Estimation on the basis of both the classified and unclassified data can be undertaken in a straightforward manner by fitting a g-component mixture model by maximum likelihood (ML) via the EM algorithm in the situation where the observed data can be assumed to be an observed random sample from the adopted mixture distribution. This assumption applies if the missing-data mechanism is ignorable in the terminology pioneered by Rubin (1976). An initial likelihood approach was to use the so-called classification ML approach whereby the missing labels are taken to be parameters to be estimated along with the parameters of the class-conditional distributions. However, as it can lead to inconsistent estimates, the focus of attention switched to the mixture ML approach after the appearance of the EM algorithm (Dempster et al., 1977). Particular attention is given here to the asymptotic relative efficiency (ARE) of the Bayes' rule estimated from a partially classified sample. Lastly, we consider briefly some recent results in situations where the missing label pattern is non-ignorable for the purposes of ML estimation for the mixture model.
Deep Gaussian Mixture Models
Nov 18, 2017



Abstract:Deep learning is a hierarchical inference method formed by subsequent multiple layers of learning able to more efficiently describe complex relationships. In this work, Deep Gaussian Mixture Models are introduced and discussed. A Deep Gaussian Mixture model (DGMM) is a network of multiple layers of latent variables, where, at each layer, the variables follow a mixture of Gaussian distributions. Thus, the deep mixture model consists of a set of nested mixtures of linear models, which globally provide a nonlinear model able to describe the data in a very flexible way. In order to avoid overparameterized solutions, dimension reduction by factor models can be applied at each layer of the architecture thus resulting in deep mixtures of factor analysers.
Iteratively-Reweighted Least-Squares Fitting of Support Vector Machines: A Majorization--Minimization Algorithm Approach
May 12, 2017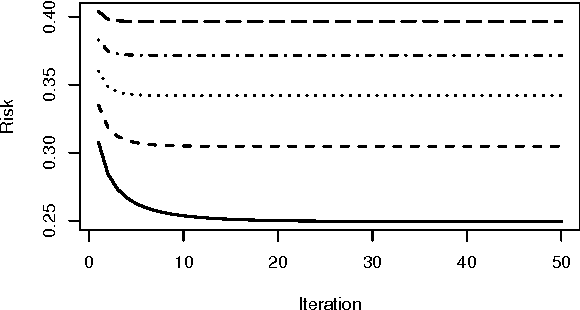
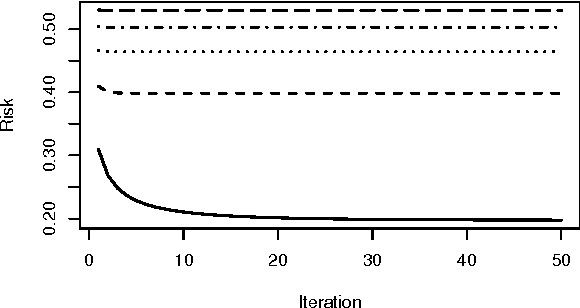
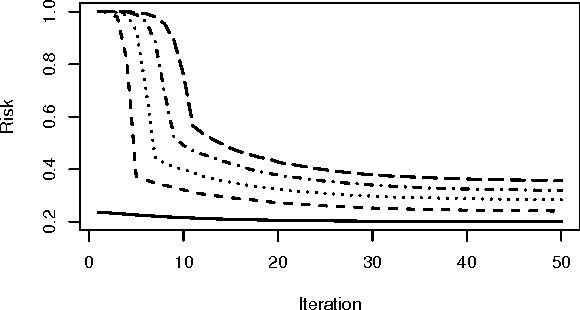
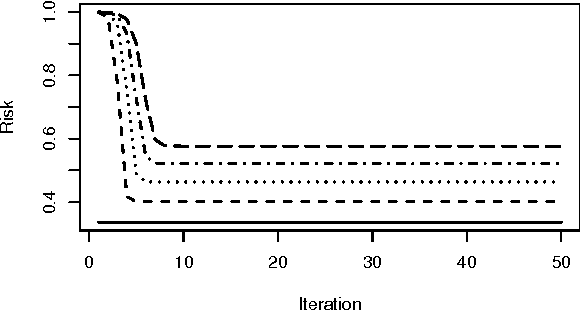
Abstract:Support vector machines (SVMs) are an important tool in modern data analysis. Traditionally, support vector machines have been fitted via quadratic programming, either using purpose-built or off-the-shelf algorithms. We present an alternative approach to SVM fitting via the majorization--minimization (MM) paradigm. Algorithms that are derived via MM algorithm constructions can be shown to monotonically decrease their objectives at each iteration, as well as be globally convergent to stationary points. We demonstrate the construction of iteratively-reweighted least-squares (IRLS) algorithms, via the MM paradigm, for SVM risk minimization problems involving the hinge, least-square, squared-hinge, and logistic losses, and 1-norm, 2-norm, and elastic net penalizations. Successful implementations of our algorithms are presented via some numerical examples.
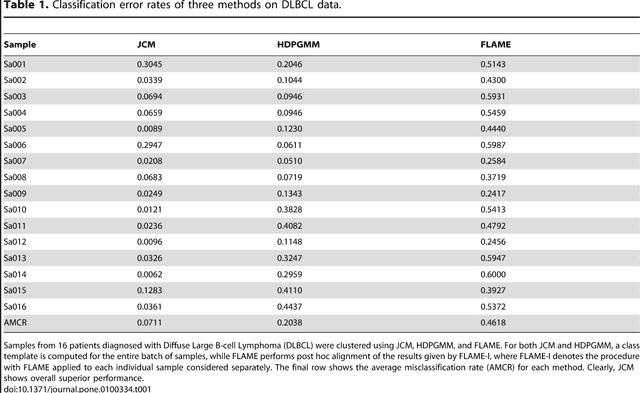
Supervised Classification of Flow Cytometric Samples via the Joint Clustering and Matching (JCM) Procedure
Nov 11, 2014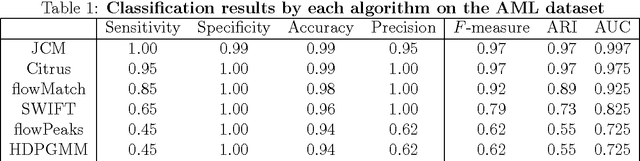
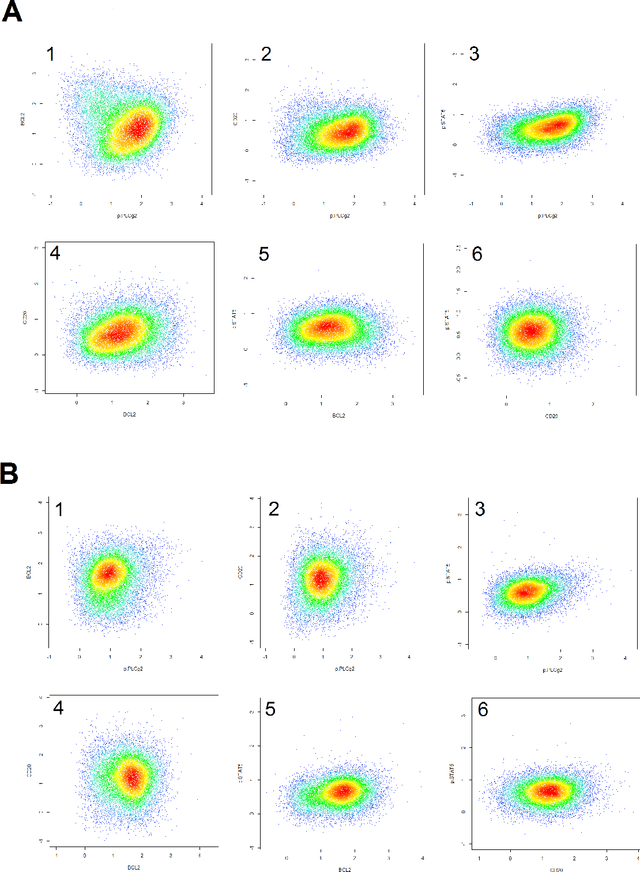
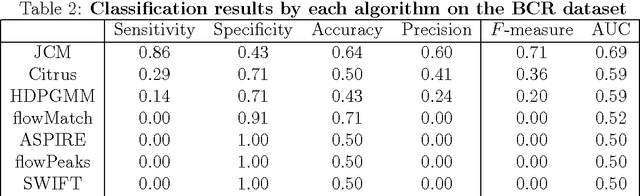
Abstract:We consider the use of the Joint Clustering and Matching (JCM) procedure for the supervised classification of a flow cytometric sample with respect to a number of predefined classes of such samples. The JCM procedure has been proposed as a method for the unsupervised classification of cells within a sample into a number of clusters and in the case of multiple samples, the matching of these clusters across the samples. The two tasks of clustering and matching of the clusters are performed simultaneously within the JCM framework. In this paper, we consider the case where there is a number of distinct classes of samples whose class of origin is known, and the problem is to classify a new sample of unknown class of origin to one of these predefined classes. For example, the different classes might correspond to the types of a particular disease or to the various health outcomes of a patient subsequent to a course of treatment. We show and demonstrate on some real datasets how the JCM procedure can be used to carry out this supervised classification task. A mixture distribution is used to model the distribution of the expressions of a fixed set of markers for each cell in a sample with the components in the mixture model corresponding to the various populations of cells in the composition of the sample. For each class of samples, a class template is formed by the adoption of random-effects terms to model the inter-sample variation within a class. The classification of a new unclassified sample is undertaken by assigning the unclassified sample to the class that minimizes the Kullback-Leibler distance between its fitted mixture density and each class density provided by the class templates.
Joint Modeling and Registration of Cell Populations in Cohorts of High-Dimensional Flow Cytometric Data
May 31, 2013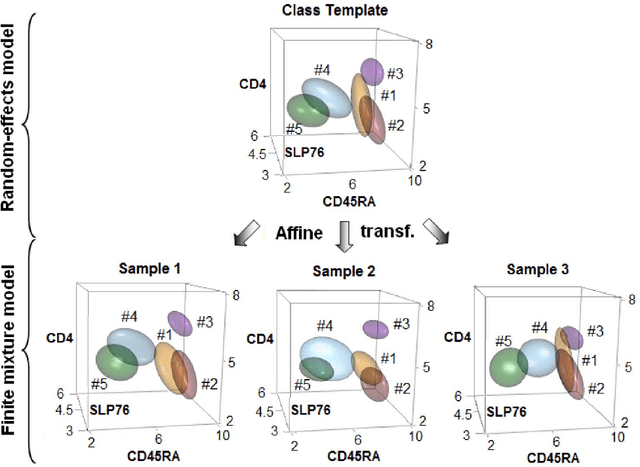
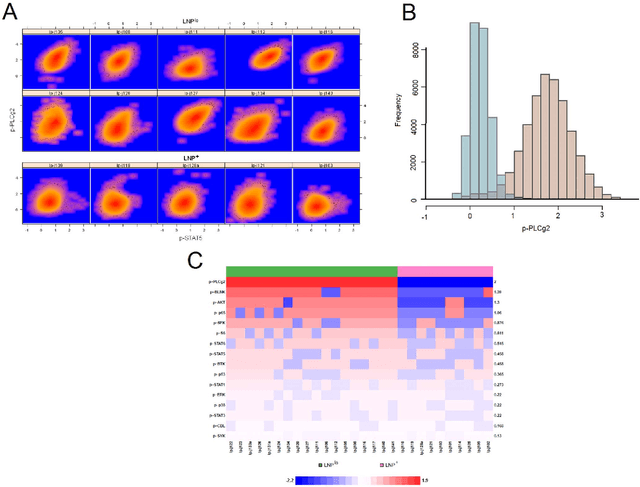
Abstract:In systems biomedicine, an experimenter encounters different potential sources of variation in data such as individual samples, multiple experimental conditions, and multi-variable network-level responses. In multiparametric cytometry, which is often used for analyzing patient samples, such issues are critical. While computational methods can identify cell populations in individual samples, without the ability to automatically match them across samples, it is difficult to compare and characterize the populations in typical experiments, such as those responding to various stimulations or distinctive of particular patients or time-points, especially when there are many samples. Joint Clustering and Matching (JCM) is a multi-level framework for simultaneous modeling and registration of populations across a cohort. JCM models every population with a robust multivariate probability distribution. Simultaneously, JCM fits a random-effects model to construct an overall batch template -- used for registering populations across samples, and classifying new samples. By tackling systems-level variation, JCM supports practical biomedical applications involving large cohorts.
Strong Consistency of Prototype Based Clustering in Probabilistic Space
Apr 19, 2010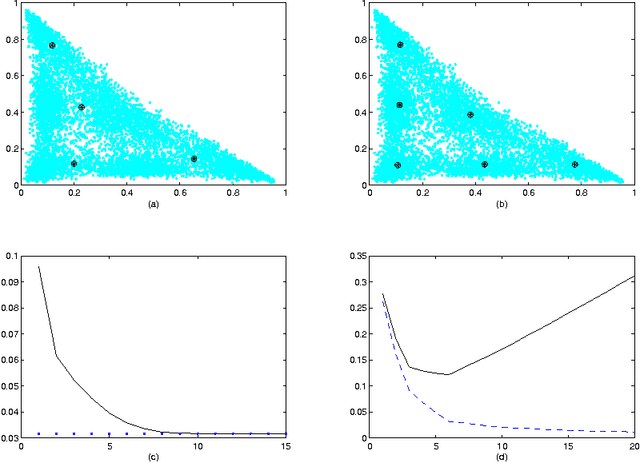
Abstract:In this paper we formulate in general terms an approach to prove strong consistency of the Empirical Risk Minimisation inductive principle applied to the prototype or distance based clustering. This approach was motivated by the Divisive Information-Theoretic Feature Clustering model in probabilistic space with Kullback-Leibler divergence which may be regarded as a special case within the Clustering Minimisation framework. Also, we propose clustering regularization restricting creation of additional clusters which are not significant or are not essentially different comparing with existing clusters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge