Estimation of Classification Rules from Partially Classified Data
Paper and Code
Apr 13, 2020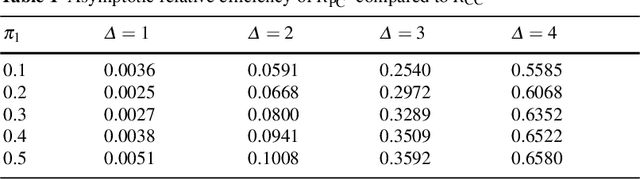
We consider the situation where the observed sample contains some observations whose class of origin is known (that is, they are classified with respect to the g underlying classes of interest), and where the remaining observations in the sample are unclassified (that is, their class labels are unknown). For class-conditional distributions taken to be known up to a vector of unknown parameters, the aim is to estimate the Bayes' rule of allocation for the allocation of subsequent unclassified observations. Estimation on the basis of both the classified and unclassified data can be undertaken in a straightforward manner by fitting a g-component mixture model by maximum likelihood (ML) via the EM algorithm in the situation where the observed data can be assumed to be an observed random sample from the adopted mixture distribution. This assumption applies if the missing-data mechanism is ignorable in the terminology pioneered by Rubin (1976). An initial likelihood approach was to use the so-called classification ML approach whereby the missing labels are taken to be parameters to be estimated along with the parameters of the class-conditional distributions. However, as it can lead to inconsistent estimates, the focus of attention switched to the mixture ML approach after the appearance of the EM algorithm (Dempster et al., 1977). Particular attention is given here to the asymptotic relative efficiency (ARE) of the Bayes' rule estimated from a partially classified sample. Lastly, we consider briefly some recent results in situations where the missing label pattern is non-ignorable for the purposes of ML estimation for the mixture model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge