Some Simulation and Empirical Results for Semi-Supervised Learning of the Bayes Rule of Allocation

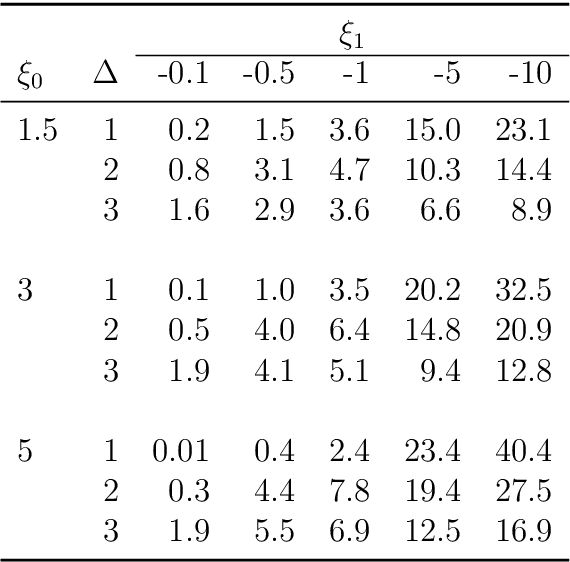
There has been increasing attention to semi-supervised learning (SSL) approaches in machine learning to forming a classifier in situations where the training data consists of some feature vectors that have their class labels missing. In this study, we consider the generative model approach proposed by Ahfock&McLachlan(2020) who introduced a framework with a missingness mechanism for the missing labels of the unclassified features. In the case of two multivariate normal classes with a common covariance matrix, they showed that the error rate of the estimated Bayes' rule formed by this SSL approach can actually have lower error rate than the one that could be formed from a completely classified sample. In this study we consider this rather surprising result in cases where there may be more than two normal classes with not necessarily common covariance matrices.

Semi-Supervised Learning of Classifiers from a Statistical Perspective: A Brief Review

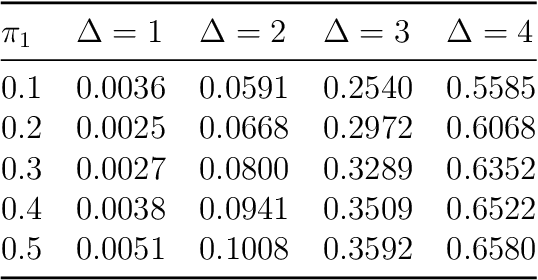
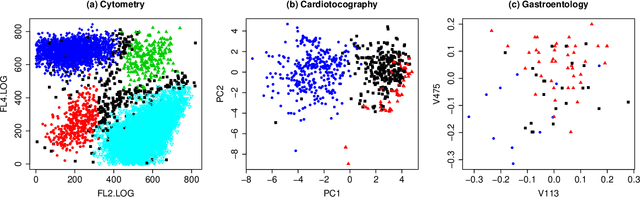
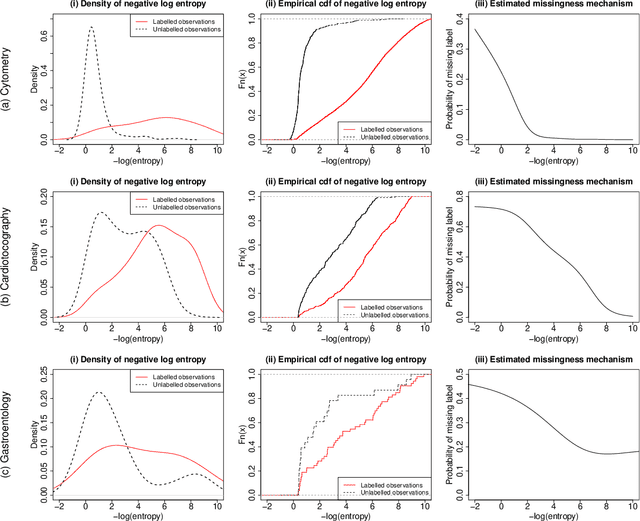
There has been increasing attention to semi-supervised learning (SSL) approaches in machine learning to forming a classifier in situations where the training data for a classifier consists of a limited number of classified observations but a much larger number of unclassified observations. This is because the procurement of classified data can be quite costly due to high acquisition costs and subsequent financial, time, and ethical issues that can arise in attempts to provide the true class labels for the unclassified data that have been acquired. We provide here a review of statistical SSL approaches to this problem, focussing on the recent result that a classifier formed from a partially classified sample can actually have smaller expected error rate than that if the sample were completely classified.

Harmless label noise and informative soft-labels in supervised classification

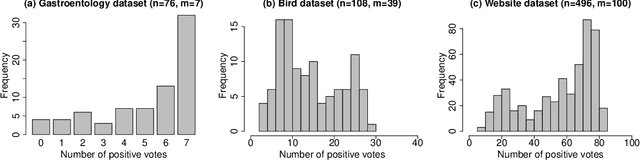
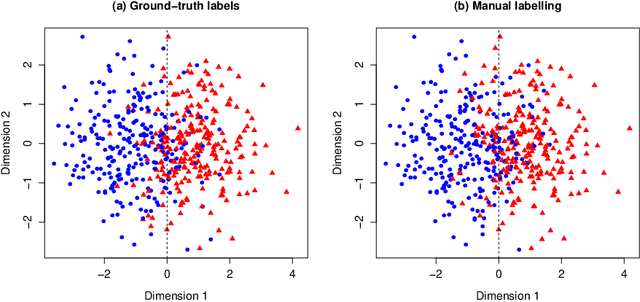
Manual labelling of training examples is common practice in supervised learning. When the labelling task is of non-trivial difficulty, the supplied labels may not be equal to the ground-truth labels, and label noise is introduced into the training dataset. If the manual annotation is carried out by multiple experts, the same training example can be given different class assignments by different experts, which is indicative of label noise. In the framework of model-based classification, a simple, but key observation is that when the manual labels are sampled using the posterior probabilities of class membership, the noisy labels are as valuable as the ground-truth labels in terms of statistical information. A relaxation of this process is a random effects model for imperfect labelling by a group that uses approximate posterior probabilities of class membership. The relative efficiency of logistic regression using the noisy labels compared to logistic regression using the ground-truth labels can then be derived. The main finding is that logistic regression can be robust to label noise when label noise and classification difficulty are positively correlated. In particular, when classification difficulty is the only source of label errors, multiple sets of noisy labels can supply more information for the estimation of a classification rule compared to the single set of ground-truth labels.

Estimation of Classification Rules from Partially Classified Data

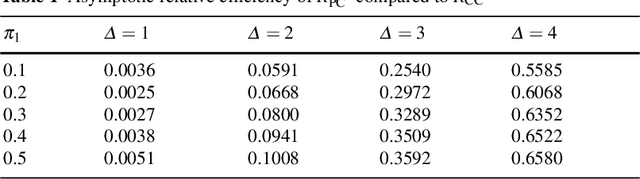
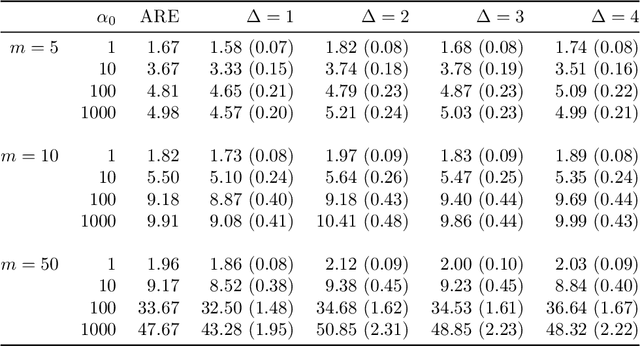
We consider the situation where the observed sample contains some observations whose class of origin is known (that is, they are classified with respect to the g underlying classes of interest), and where the remaining observations in the sample are unclassified (that is, their class labels are unknown). For class-conditional distributions taken to be known up to a vector of unknown parameters, the aim is to estimate the Bayes' rule of allocation for the allocation of subsequent unclassified observations. Estimation on the basis of both the classified and unclassified data can be undertaken in a straightforward manner by fitting a g-component mixture model by maximum likelihood (ML) via the EM algorithm in the situation where the observed data can be assumed to be an observed random sample from the adopted mixture distribution. This assumption applies if the missing-data mechanism is ignorable in the terminology pioneered by Rubin (1976). An initial likelihood approach was to use the so-called classification ML approach whereby the missing labels are taken to be parameters to be estimated along with the parameters of the class-conditional distributions. However, as it can lead to inconsistent estimates, the focus of attention switched to the mixture ML approach after the appearance of the EM algorithm (Dempster et al., 1977). Particular attention is given here to the asymptotic relative efficiency (ARE) of the Bayes' rule estimated from a partially classified sample. Lastly, we consider briefly some recent results in situations where the missing label pattern is non-ignorable for the purposes of ML estimation for the mixture model.

Distributed Bayesian Computation for Model Choice

We propose a general method for distributed Bayesian model choice, where each worker has access only to non-overlapping subsets of the data. Our approach approximates the model evidence for the full data set through Monte Carlo sampling from the posterior on every subset generating a model evidence per subset. The model evidences per worker are then consistently combined using a novel approach which corrects for the splitting using summary statistics of the generated samples. This divide-and-conquer approach allows Bayesian model choice in the large data setting, exploiting all available information but limiting communication between workers. Our work thereby complements the work on consensus Monte Carlo (Scott et al., 2016) by explicitly enabling model choice. In addition, we show how the suggested approach can be extended to model choice within a reversible jump setting that explores multiple models within one run.