Hien D. Nguyen
HDC: Hierarchical Distillation for Multi-level Noisy Consistency in Semi-Supervised Fetal Ultrasound Segmentation
Apr 14, 2025Abstract:Transvaginal ultrasound is a critical imaging modality for evaluating cervical anatomy and detecting physiological changes. However, accurate segmentation of cervical structures remains challenging due to low contrast, shadow artifacts, and fuzzy boundaries. While convolutional neural networks (CNNs) have shown promising results in medical image segmentation, their performance is often limited by the need for large-scale annotated datasets - an impractical requirement in clinical ultrasound imaging. Semi-supervised learning (SSL) offers a compelling solution by leveraging unlabeled data, but existing teacher-student frameworks often suffer from confirmation bias and high computational costs. We propose HDC, a novel semi-supervised segmentation framework that integrates Hierarchical Distillation and Consistency learning within a multi-level noise mean-teacher framework. Unlike conventional approaches that rely solely on pseudo-labeling, we introduce a hierarchical distillation mechanism that guides feature-level learning via two novel objectives: (1) Correlation Guidance Loss to align feature representations between the teacher and main student branch, and (2) Mutual Information Loss to stabilize representations between the main and noisy student branches. Our framework reduces model complexity while improving generalization. Extensive experiments on two fetal ultrasound datasets, FUGC and PSFH, demonstrate that our method achieves competitive performance with significantly lower computational overhead than existing multi-teacher models.
Ontology-based Solution for Building an Intelligent Searching System on Traffic Law Documents
Jan 26, 2023



Abstract:In this paper, an ontology-based approach is used to organize the knowledge base of legal documents in road traffic law. This knowledge model is built by the improvement of ontology Rela-model. In addition, several searching problems on traffic law are proposed and solved based on the legal knowledge base. The intelligent search system on Vietnam road traffic law is constructed by applying the method. The searching system can help users to find concepts and definitions in road traffic law. Moreover, it can also determine penalties and fines for violations in the traffic. The experiment results show that the system is efficient for users' typical searching and is emerging for usage in the real-world.
Regularized Estimation and Feature Selection in Mixtures of Gaussian-Gated Experts Models
Sep 12, 2019



Abstract:Mixtures-of-Experts models and their maximum likelihood estimation (MLE) via the EM algorithm have been thoroughly studied in the statistics and machine learning literature. They are subject of a growing investigation in the context of modeling with high-dimensional predictors with regularized MLE. We examine MoE with Gaussian gating network, for clustering and regression, and propose an $\ell_1$-regularized MLE to encourage sparse models and deal with the high-dimensional setting. We develop an EM-Lasso algorithm to perform parameter estimation and utilize a BIC-like criterion to select the model parameters, including the sparsity tuning hyperparameters. Experiments conducted on simulated data show the good performance of the proposed regularized MLE compared to the standard MLE with the EM algorithm.
Approximate Bayesian computation via the energy statistic
May 14, 2019



Abstract:Approximate Bayesian computation (ABC) has become an essential part of the Bayesian toolbox for addressing problems in which the likelihood is prohibitively expensive or entirely unknown, making it intractable. ABC defines a quasi-posterior by comparing observed data with simulated data, traditionally based on some summary statistics, the elicitation of which is regarded as a key difficulty. In recent years, a number of data discrepancy measures bypassing the construction of summary statistics have been proposed, including the Kullback--Leibler divergence, the Wasserstein distance and maximum mean discrepancies. Here we propose a novel importance-sampling (IS) ABC algorithm relying on the so-called \textit{two-sample energy statistic}. We establish a new asymptotic result for the case where both the observed sample size and the simulated data sample size increase to infinity, which highlights to what extent the data discrepancy measure impacts the asymptotic pseudo-posterior. The result holds in the broad setting of IS-ABC methodologies, thus generalizing previous results that have been established only for rejection ABC algorithms. Furthermore, we propose a consistent V-statistic estimator of the energy statistic, under which we show that the large sample result holds. Our proposed energy statistic based ABC algorithm is demonstrated on a variety of models, including a Gaussian mixture, a moving-average model of order two, a bivariate beta and a multivariate $g$-and-$k$ distribution. We find that our proposed method compares well with alternative discrepancy measures.
Partial Evaluation of Logic Programs in Vector Spaces
Nov 28, 2018
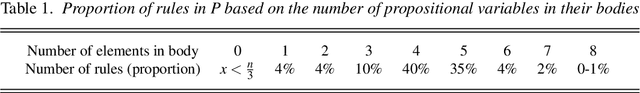

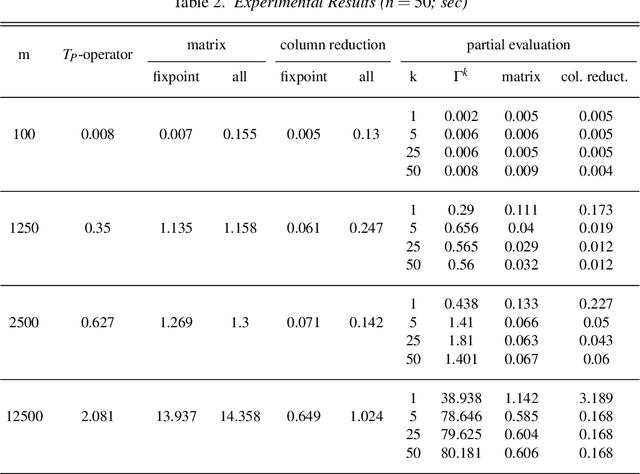
Abstract:In this paper, we introduce methods of encoding propositional logic programs in vector spaces. Interpretations are represented by vectors and programs are represented by matrices. The least model of a definite program is computed by multiplying an interpretation vector and a program matrix. To optimize computation in vector spaces, we provide a method of partial evaluation of programs using linear algebra. Partial evaluation is done by unfolding rules in a program, and it is realized in a vector space by multiplying program matrices. We perform experiments using randomly generated programs and show that partial evaluation has potential for realizing efficient computation in huge scale of programs.
Model-Based Clustering and Classification of Functional Data
Mar 02, 2018



Abstract:The problem of complex data analysis is a central topic of modern statistical science and learning systems and is becoming of broader interest with the increasing prevalence of high-dimensional data. The challenge is to develop statistical models and autonomous algorithms that are able to acquire knowledge from raw data for exploratory analysis, which can be achieved through clustering techniques or to make predictions of future data via classification (i.e., discriminant analysis) techniques. Latent data models, including mixture model-based approaches are one of the most popular and successful approaches in both the unsupervised context (i.e., clustering) and the supervised one (i.e, classification or discrimination). Although traditionally tools of multivariate analysis, they are growing in popularity when considered in the framework of functional data analysis (FDA). FDA is the data analysis paradigm in which the individual data units are functions (e.g., curves, surfaces), rather than simple vectors. In many areas of application, the analyzed data are indeed often available in the form of discretized values of functions or curves (e.g., time series, waveforms) and surfaces (e.g., 2d-images, spatio-temporal data). This functional aspect of the data adds additional difficulties compared to the case of a classical multivariate (non-functional) data analysis. We review and present approaches for model-based clustering and classification of functional data. We derive well-established statistical models along with efficient algorithmic tools to address problems regarding the clustering and the classification of these high-dimensional data, including their heterogeneity, missing information, and dynamical hidden structure. The presented models and algorithms are illustrated on real-world functional data analysis problems from several application area.
An Introduction to the Practical and Theoretical Aspects of Mixture-of-Experts Modeling
Jul 12, 2017



Abstract:Mixture-of-experts (MoE) models are a powerful paradigm for modeling of data arising from complex data generating processes (DGPs). In this article, we demonstrate how different MoE models can be constructed to approximate the underlying DGPs of arbitrary types of data. Due to the probabilistic nature of MoE models, we propose the maximum quasi-likelihood (MQL) estimator as a method for estimating MoE model parameters from data, and we provide conditions under which MQL estimators are consistent and asymptotically normal. The blockwise minorization-maximizatoin (blockwise-MM) algorithm framework is proposed as an all-purpose method for constructing algorithms for obtaining MQL estimators. An example derivation of a blockwise-MM algorithm is provided. We then present a method for constructing information criteria for estimating the number of components in MoE models and provide justification for the classic Bayesian information criterion (BIC). We explain how MoE models can be used to conduct classification, clustering, and regression and we illustrate these applications via a pair of worked examples.
Iteratively-Reweighted Least-Squares Fitting of Support Vector Machines: A Majorization--Minimization Algorithm Approach
May 12, 2017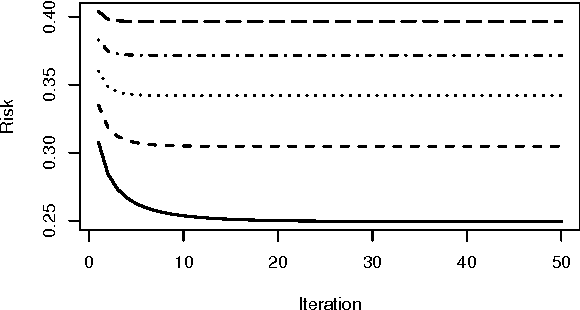
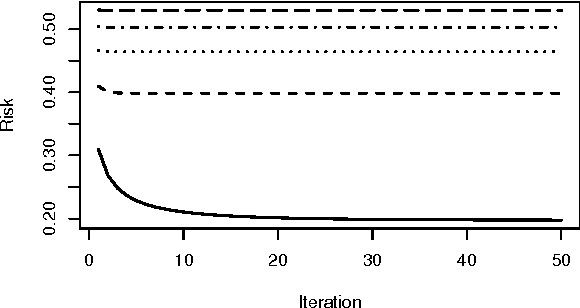
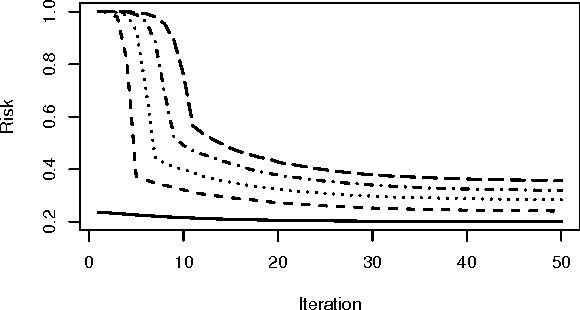
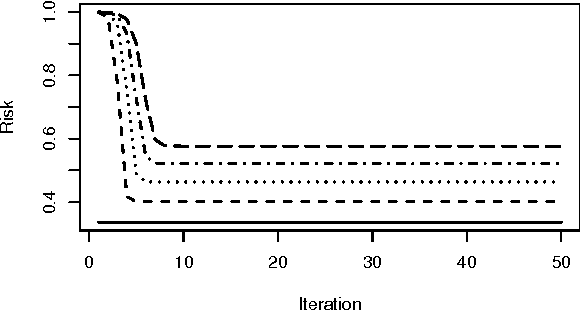
Abstract:Support vector machines (SVMs) are an important tool in modern data analysis. Traditionally, support vector machines have been fitted via quadratic programming, either using purpose-built or off-the-shelf algorithms. We present an alternative approach to SVM fitting via the majorization--minimization (MM) paradigm. Algorithms that are derived via MM algorithm constructions can be shown to monotonically decrease their objectives at each iteration, as well as be globally convergent to stationary points. We demonstrate the construction of iteratively-reweighted least-squares (IRLS) algorithms, via the MM paradigm, for SVM risk minimization problems involving the hinge, least-square, squared-hinge, and logistic losses, and 1-norm, 2-norm, and elastic net penalizations. Successful implementations of our algorithms are presented via some numerical examples.
An Introduction to MM Algorithms for Machine Learning and Statistical
Nov 12, 2016



Abstract:MM (majorization--minimization) algorithms are an increasingly popular tool for solving optimization problems in machine learning and statistical estimation. This article introduces the MM algorithm framework in general and via three popular example applications: Gaussian mixture regressions, multinomial logistic regressions, and support vector machines. Specific algorithms for the three examples are derived and numerical demonstrations are presented. Theoretical and practical aspects of MM algorithm design are discussed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge