Towards end-to-end ASP computation

We propose an end-to-end approach for answer set programming (ASP) and linear algebraically compute stable models satisfying given constraints. The idea is to implement Lin-Zhao's theorem \cite{Lin04} together with constraints directly in vector spaces as numerical minimization of a cost function constructed from a matricized normal logic program, loop formulas in Lin-Zhao's theorem and constraints, thereby no use of symbolic ASP or SAT solvers involved in our approach. We also propose precomputation that shrinks the program size and heuristics for loop formulas to reduce computational difficulty. We empirically test our approach with programming examples including the 3-coloring and Hamiltonian cycle problems. As our approach is purely numerical and only contains vector/matrix operations, acceleration by parallel technologies such as many-cores and GPUs is expected.

MatSat: a matrix-based differentiable SAT solver

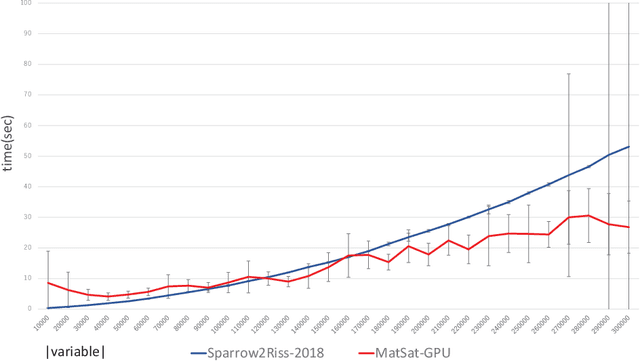
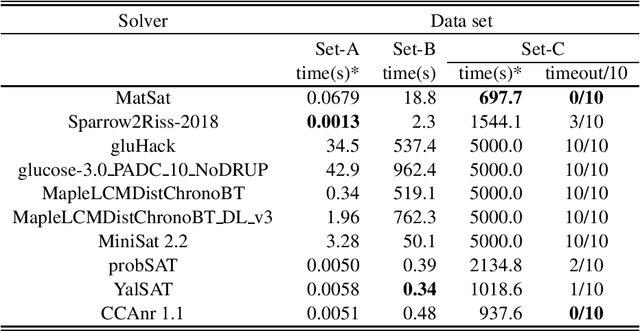
We propose a new approach to SAT solving which solves SAT problems in vector spaces as a cost minimization problem of a non-negative differentiable cost function J^sat. In our approach, a solution, i.e., satisfying assignment, for a SAT problem in n variables is represented by a binary vector u in {0,1}^n that makes J^sat(u) zero. We search for such u in a vector space R^n by cost minimization, i.e., starting from an initial u_0 and minimizing J to zero while iteratively updating u by Newton's method. We implemented our approach as a matrix-based differential SAT solver MatSat. Although existing main-stream SAT solvers decide each bit of a solution assignment one by one, be they of conflict driven clause learning (CDCL) type or of stochastic local search (SLS) type, MatSat fundamentally differs from them in that it continuously approach a solution in a vector space. We conducted an experiment to measure the scalability of MatSat with random 3-SAT problems in which MatSat could find a solution up to n=10^5 variables. We also compared MatSat with four state-of-the-art SAT solvers including winners of SAT competition 2018 and SAT Race 2019 in terms of time for finding a solution, using a random benchmark set from SAT 2018 competition and an artificial random 3-SAT instance set. The result shows that MatSat comes in second in both test sets and outperforms all the CDCL type solvers.

A tensorized logic programming language for large-scale data

We introduce a new logic programming language T-PRISM based on tensor embeddings. Our embedding scheme is a modification of the distribution semantics in PRISM, one of the state-of-the-art probabilistic logic programming languages, by replacing distribution functions with multidimensional arrays, i.e., tensors. T-PRISM consists of two parts: logic programming part and numerical computation part. The former provides flexible and interpretable modeling at the level of first order logic, and the latter part provides scalable computation utilizing parallelization and hardware acceleration with GPUs. Combing these two parts provides a remarkably wide range of high-level declarative modeling from symbolic reasoning to deep learning. To embody this programming language, we also introduce a new semantics, termed tensorized semantics, which combines the traditional least model semantics in logic programming with the embeddings of tensors. In T-PRISM, we first derive a set of equations related to tensors from a given program using logical inference, i.e., Prolog execution in a symbolic space and then solve the derived equations in a continuous space by TensorFlow. Using our preliminary implementation of T-PRISM, we have successfully dealt with a wide range of modeling. We have succeeded in dealing with real large-scale data in the declarative modeling. This paper presents a DistMult model for knowledge graphs using the FB15k and WN18 datasets.

Partial Evaluation of Logic Programs in Vector Spaces

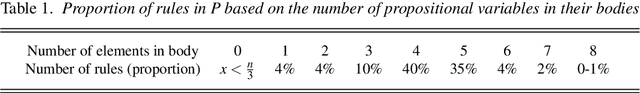
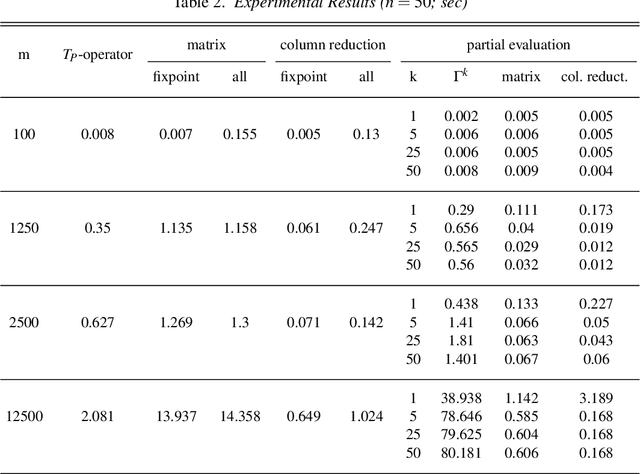
In this paper, we introduce methods of encoding propositional logic programs in vector spaces. Interpretations are represented by vectors and programs are represented by matrices. The least model of a definite program is computed by multiplying an interpretation vector and a program matrix. To optimize computation in vector spaces, we provide a method of partial evaluation of programs using linear algebra. Partial evaluation is done by unfolding rules in a program, and it is realized in a vector space by multiplying program matrices. We perform experiments using randomly generated programs and show that partial evaluation has potential for realizing efficient computation in huge scale of programs.

Embedding Tarskian Semantics in Vector Spaces

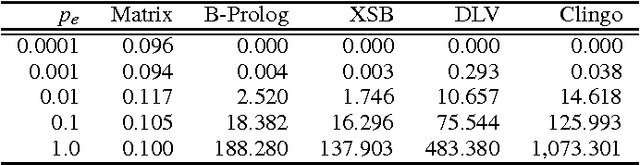
We propose a new linear algebraic approach to the computation of Tarskian semantics in logic. We embed a finite model M in first-order logic with N entities in N-dimensional Euclidean space R^N by mapping entities of M to N dimensional one-hot vectors and k-ary relations to order-k adjacency tensors (multi-way arrays). Second given a logical formula F in prenex normal form, we compile F into a set Sigma_F of algebraic formulas in multi-linear algebra with a nonlinear operation. In this compilation, existential quantifiers are compiled into a specific type of tensors, e.g., identity matrices in the case of quantifying two occurrences of a variable. It is shown that a systematic evaluation of Sigma_F in R^N gives the truth value, 1(true) or 0(false), of F in M. Based on this framework, we also propose an unprecedented way of computing the least models defined by Datalog programs in linear spaces via matrix equations and empirically show its effectiveness compared to state-of-the-art approaches.

A Linear Algebraic Approach to Datalog Evaluation

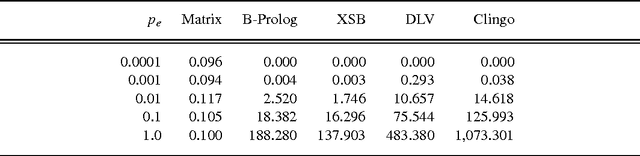
In this paper, we propose a fundamentally new approach to Datalog evaluation. Given a linear Datalog program DB written using N constants and binary predicates, we first translate if-and-only-if completions of clauses in DB into a set Eq(DB) of matrix equations with a non-linear operation where relations in M_DB, the least Herbrand model of DB, are encoded as adjacency matrices. We then translate Eq(DB) into another, but purely linear matrix equations tilde_Eq(DB). It is proved that the least solution of tilde_Eq(DB) in the sense of matrix ordering is converted to the least solution of Eq(DB) and the latter gives M_DB as a set of adjacency matrices. Hence computing the least solution of tilde_Eq(DB) is equivalent to computing M_DB specified by DB. For a class of tail recursive programs and for some other types of programs, our approach achieves O(N^3) time complexity irrespective of the number of variables in a clause since only matrix operations costing O(N^3) or less are used. We conducted two experiments that compute the least Herbrand models of linear Datalog programs. The first experiment computes transitive closure of artificial data and real network data taken from the Koblenz Network Collection. The second one compared the proposed approach with the state-of-the-art symbolic systems including two Prolog systems and two ASP systems, in terms of computation time for a transitive closure program and the same generation program. In the experiment, it is observed that our linear algebraic approach runs 10^1 ~ 10^4 times faster than the symbolic systems when data is not sparse. To appear in Theory and Practice of Logic Programming (TPLP).

A Logic-based Approach to Generatively Defined Discriminative Modeling

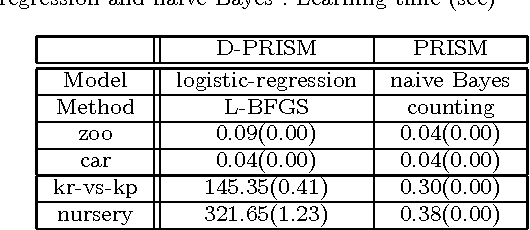
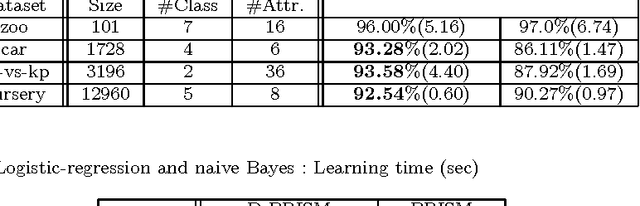
Conditional random fields (CRFs) are usually specified by graphical models but in this paper we propose to use probabilistic logic programs and specify them generatively. Our intension is first to provide a unified approach to CRFs for complex modeling through the use of a Turing complete language and second to offer a convenient way of realizing generative-discriminative pairs in machine learning to compare generative and discriminative models and choose the best model. We implemented our approach as the D-PRISM language by modifying PRISM, a logic-based probabilistic modeling language for generative modeling, while exploiting its dynamic programming mechanism for efficient probability computation. We tested D-PRISM with logistic regression, a linear-chain CRF and a CRF-CFG and empirically confirmed their excellent discriminative performance compared to their generative counterparts, i.e.\ naive Bayes, an HMM and a PCFG. We also introduced new CRF models, CRF-BNCs and CRF-LCGs. They are CRF versions of Bayesian network classifiers and probabilistic left-corner grammars respectively and easily implementable in D-PRISM. We empirically showed that they outperform their generative counterparts as expected.

Viterbi training in PRISM

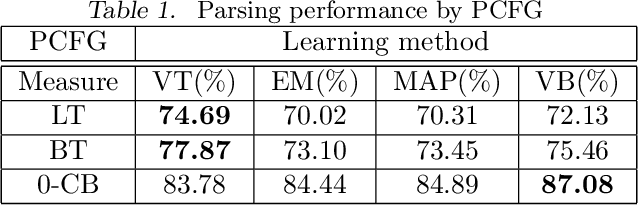
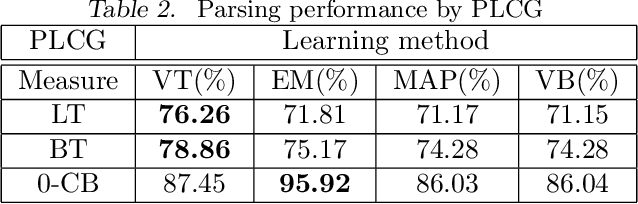
VT (Viterbi training), or hard EM, is an efficient way of parameter learning for probabilistic models with hidden variables. Given an observation $y$, it searches for a state of hidden variables $x$ that maximizes $p(x,y \mid \theta)$ by coordinate ascent on parameters $\theta$ and $x$. In this paper we introduce VT to PRISM, a logic-based probabilistic modeling system for generative models. VT improves PRISM in three ways. First VT in PRISM converges faster than EM in PRISM due to the VT's termination condition. Second, parameters learned by VT often show good prediction performance compared to those learned by EM. We conducted two parsing experiments with probabilistic grammars while learning parameters by a variety of inference methods, i.e.\ VT, EM, MAP and VB. The result is that VT achieved the best parsing accuracy among them in both experiments. Also we conducted a similar experiment for classification tasks where a hidden variable is not a prediction target unlike probabilistic grammars. We found that in such a case VT does not necessarily yield superior performance. Third since VT always deals with a single probability of a single explanation, Viterbi explanation, the exclusiveness condition that is imposed on PRISM programs is no more required if we learn parameters by VT. Last but not least we can say that as VT in PRISM is general and applicable to any PRISM program, it largely reduces the need for the user to develop a specific VT algorithm for a specific model. Furthermore since VT in PRISM can be used just by setting a PRISM flag appropriately, it makes VT easily accessible to (probabilistic) logic programmers. To appear in Theory and Practice of Logic Programming (TPLP).

Verbal Characterization of Probabilistic Clusters using Minimal Discriminative Propositions

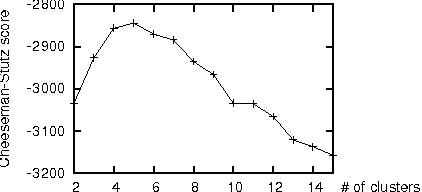
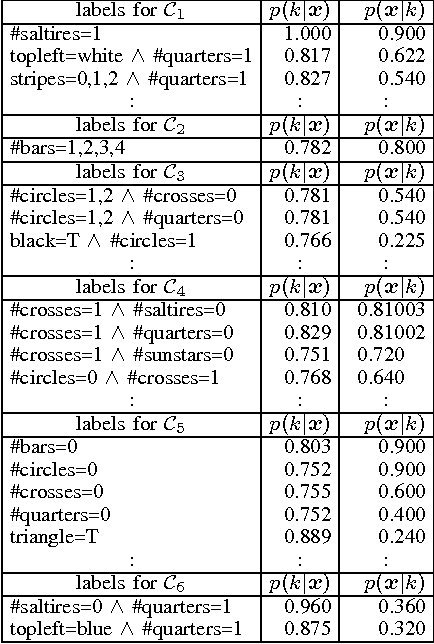
In a knowledge discovery process, interpretation and evaluation of the mined results are indispensable in practice. In the case of data clustering, however, it is often difficult to see in what aspect each cluster has been formed. This paper proposes a method for automatic and objective characterization or "verbalization" of the clusters obtained by mixture models, in which we collect conjunctions of propositions (attribute-value pairs) that help us interpret or evaluate the clusters. The proposed method provides us with a new, in-depth and consistent tool for cluster interpretation/evaluation, and works for various types of datasets including continuous attributes and missing values. Experimental results with a couple of standard datasets exhibit the utility of the proposed method, and the importance of the feedbacks from the interpretation/evaluation step.

CHR(PRISM)-based Probabilistic Logic Learning

PRISM is an extension of Prolog with probabilistic predicates and built-in support for expectation-maximization learning. Constraint Handling Rules (CHR) is a high-level programming language based on multi-headed multiset rewrite rules. In this paper, we introduce a new probabilistic logic formalism, called CHRiSM, based on a combination of CHR and PRISM. It can be used for high-level rapid prototyping of complex statistical models by means of "chance rules". The underlying PRISM system can then be used for several probabilistic inference tasks, including probability computation and parameter learning. We define the CHRiSM language in terms of syntax and operational semantics, and illustrate it with examples. We define the notion of ambiguous programs and define a distribution semantics for unambiguous programs. Next, we describe an implementation of CHRiSM, based on CHR(PRISM). We discuss the relation between CHRiSM and other probabilistic logic programming languages, in particular PCHR. Finally we identify potential application domains.