Subjective Visual Quality Assessment for High-Fidelity Learning-Based Image Compression

Learning-based image compression methods have recently emerged as promising alternatives to traditional codecs, offering improved rate-distortion performance and perceptual quality. JPEG AI represents the latest standardized framework in this domain, leveraging deep neural networks for high-fidelity image reconstruction. In this study, we present a comprehensive subjective visual quality assessment of JPEG AI-compressed images using the JPEG AIC-3 methodology, which quantifies perceptual differences in terms of Just Noticeable Difference (JND) units. We generated a dataset of 50 compressed images with fine-grained distortion levels from five diverse sources. A large-scale crowdsourced experiment collected 96,200 triplet responses from 459 participants. We reconstructed JND-based quality scales using a unified model based on boosted and plain triplet comparisons. Additionally, we evaluated the alignment of multiple objective image quality metrics with human perception in the high-fidelity range. The CVVDP metric achieved the overall highest performance; however, most metrics including CVVDP were overly optimistic in predicting the quality of JPEG AI-compressed images. These findings emphasize the necessity for rigorous subjective evaluations in the development and benchmarking of modern image codecs, particularly in the high-fidelity range. Another technical contribution is the introduction of the well-known Meng-Rosenthal-Rubin statistical test to the field of Quality of Experience research. This test can reliably assess the significance of difference in performance of quality metrics in terms of correlation between metrics and ground truth. The complete dataset, including all subjective scores, is publicly available at https://github.com/jpeg-aic/dataset-JPEG-AI-SDR25.

Fine-grained subjective visual quality assessment for high-fidelity compressed images

Advances in image compression, storage, and display technologies have made high-quality images and videos widely accessible. At this level of quality, distinguishing between compressed and original content becomes difficult, highlighting the need for assessment methodologies that are sensitive to even the smallest visual quality differences. Conventional subjective visual quality assessments often use absolute category rating scales, ranging from ``excellent'' to ``bad''. While suitable for evaluating more pronounced distortions, these scales are inadequate for detecting subtle visual differences. The JPEG standardization project AIC is currently developing a subjective image quality assessment methodology for high-fidelity images. This paper presents the proposed assessment methods, a dataset of high-quality compressed images, and their corresponding crowdsourced visual quality ratings. It also outlines a data analysis approach that reconstructs quality scale values in just noticeable difference (JND) units. The assessment method uses boosting techniques on visual stimuli to help observers detect compression artifacts more clearly. This is followed by a rescaling process that adjusts the boosted quality values back to the original perceptual scale. This reconstruction yields a fine-grained, high-precision quality scale in JND units, providing more informative results for practical applications. The dataset and code to reproduce the results will be available at https://github.com/jpeg-aic/dataset-BTC-PTC-24.

CHR(PRISM)-based Probabilistic Logic Learning

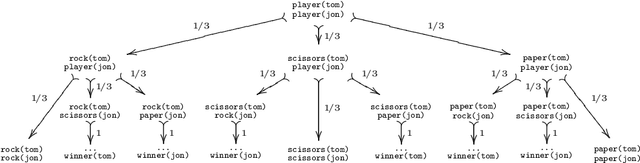
PRISM is an extension of Prolog with probabilistic predicates and built-in support for expectation-maximization learning. Constraint Handling Rules (CHR) is a high-level programming language based on multi-headed multiset rewrite rules. In this paper, we introduce a new probabilistic logic formalism, called CHRiSM, based on a combination of CHR and PRISM. It can be used for high-level rapid prototyping of complex statistical models by means of "chance rules". The underlying PRISM system can then be used for several probabilistic inference tasks, including probability computation and parameter learning. We define the CHRiSM language in terms of syntax and operational semantics, and illustrate it with examples. We define the notion of ambiguous programs and define a distribution semantics for unambiguous programs. Next, we describe an implementation of CHRiSM, based on CHR(PRISM). We discuss the relation between CHRiSM and other probabilistic logic programming languages, in particular PCHR. Finally we identify potential application domains.