Partial Evaluation of Logic Programs in Vector Spaces
Paper and Code
Nov 28, 2018
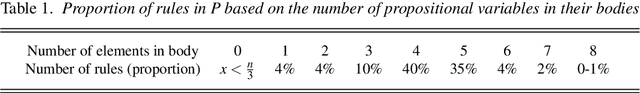

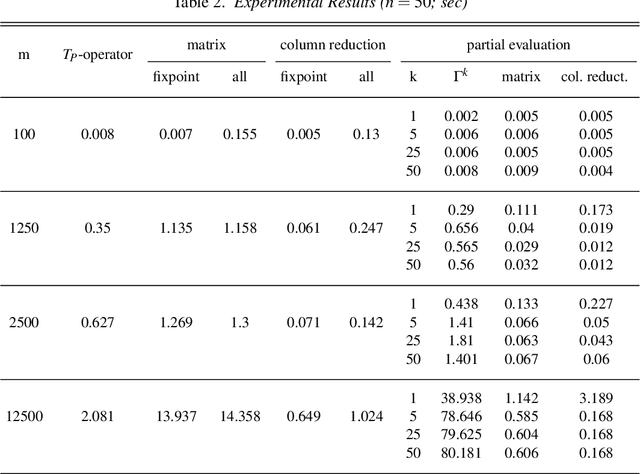
In this paper, we introduce methods of encoding propositional logic programs in vector spaces. Interpretations are represented by vectors and programs are represented by matrices. The least model of a definite program is computed by multiplying an interpretation vector and a program matrix. To optimize computation in vector spaces, we provide a method of partial evaluation of programs using linear algebra. Partial evaluation is done by unfolding rules in a program, and it is realized in a vector space by multiplying program matrices. We perform experiments using randomly generated programs and show that partial evaluation has potential for realizing efficient computation in huge scale of programs.
* Proceedings of the 11th Workshop on Answer Set Programming and Other
Computing Paradigms 2018
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge