A Logic-based Approach to Generatively Defined Discriminative Modeling

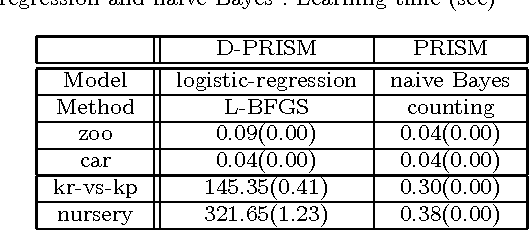
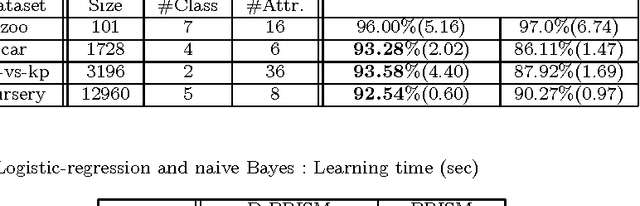
Conditional random fields (CRFs) are usually specified by graphical models but in this paper we propose to use probabilistic logic programs and specify them generatively. Our intension is first to provide a unified approach to CRFs for complex modeling through the use of a Turing complete language and second to offer a convenient way of realizing generative-discriminative pairs in machine learning to compare generative and discriminative models and choose the best model. We implemented our approach as the D-PRISM language by modifying PRISM, a logic-based probabilistic modeling language for generative modeling, while exploiting its dynamic programming mechanism for efficient probability computation. We tested D-PRISM with logistic regression, a linear-chain CRF and a CRF-CFG and empirically confirmed their excellent discriminative performance compared to their generative counterparts, i.e.\ naive Bayes, an HMM and a PCFG. We also introduced new CRF models, CRF-BNCs and CRF-LCGs. They are CRF versions of Bayesian network classifiers and probabilistic left-corner grammars respectively and easily implementable in D-PRISM. We empirically showed that they outperform their generative counterparts as expected.

Viterbi training in PRISM

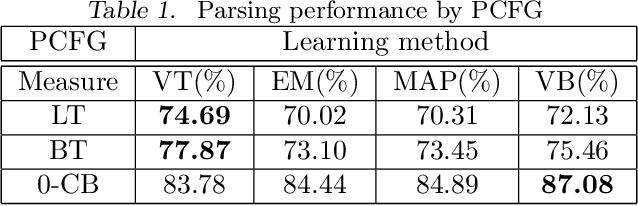
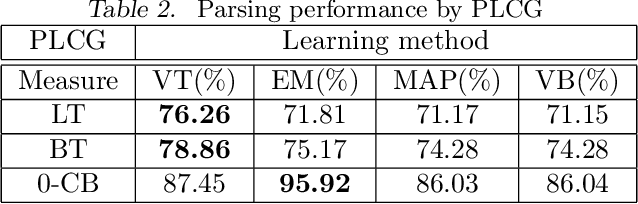
VT (Viterbi training), or hard EM, is an efficient way of parameter learning for probabilistic models with hidden variables. Given an observation $y$, it searches for a state of hidden variables $x$ that maximizes $p(x,y \mid \theta)$ by coordinate ascent on parameters $\theta$ and $x$. In this paper we introduce VT to PRISM, a logic-based probabilistic modeling system for generative models. VT improves PRISM in three ways. First VT in PRISM converges faster than EM in PRISM due to the VT's termination condition. Second, parameters learned by VT often show good prediction performance compared to those learned by EM. We conducted two parsing experiments with probabilistic grammars while learning parameters by a variety of inference methods, i.e.\ VT, EM, MAP and VB. The result is that VT achieved the best parsing accuracy among them in both experiments. Also we conducted a similar experiment for classification tasks where a hidden variable is not a prediction target unlike probabilistic grammars. We found that in such a case VT does not necessarily yield superior performance. Third since VT always deals with a single probability of a single explanation, Viterbi explanation, the exclusiveness condition that is imposed on PRISM programs is no more required if we learn parameters by VT. Last but not least we can say that as VT in PRISM is general and applicable to any PRISM program, it largely reduces the need for the user to develop a specific VT algorithm for a specific model. Furthermore since VT in PRISM can be used just by setting a PRISM flag appropriately, it makes VT easily accessible to (probabilistic) logic programmers. To appear in Theory and Practice of Logic Programming (TPLP).