Functional mixture-of-experts for classification

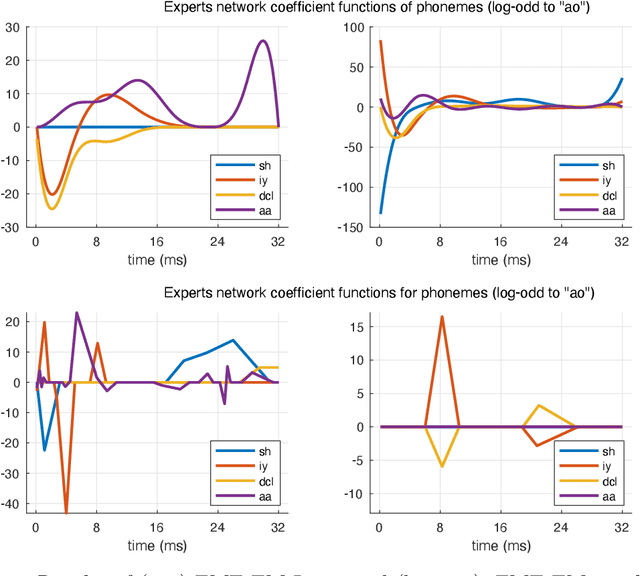
We develop a mixtures-of-experts (ME) approach to the multiclass classification where the predictors are univariate functions. It consists of a ME model in which both the gating network and the experts network are constructed upon multinomial logistic activation functions with functional inputs. We perform a regularized maximum likelihood estimation in which the coefficient functions enjoy interpretable sparsity constraints on targeted derivatives. We develop an EM-Lasso like algorithm to compute the regularized MLE and evaluate the proposed approach on simulated and real data.

Spectral image clustering on dual-energy CT scans using functional regression mixtures

Dual-energy computed tomography (DECT) is an advanced CT scanning technique enabling material characterization not possible with conventional CT scans. It allows the reconstruction of energy decay curves at each 3D image voxel, representing varying image attenuation at different effective scanning energy levels. In this paper, we develop novel functional data analysis (FDA) techniques and adapt them to the analysis of DECT decay curves. More specifically, we construct functional mixture models that integrate spatial context in mixture weights, with mixture component densities being constructed upon the energy decay curves as functional observations. We design unsupervised clustering algorithms by developing dedicated expectation maximization (EM) algorithms for the maximum likelihood estimation of the model parameters. To our knowledge, this is the first article to adapt statistical FDA tools and model-based clustering to take advantage of the full spectral information provided by DECT. We evaluate our methods on 91 head and neck cancer DECT scans. We compare our unsupervised clustering results to tumor contours traced manually by radiologists, as well as to several baseline algorithms. Given the inter-rater variability even among experts at delineating head and neck tumors, and given the potential importance of tissue reactions surrounding the tumor itself, our proposed methodology has the potential to add value in downstream machine learning applications for clinical outcome prediction based on DECT data in head and neck cancer.

Non-asymptotic model selection in block-diagonal mixture of polynomial experts models

Model selection, via penalized likelihood type criteria, is a standard task in many statistical inference and machine learning problems. Progress has led to deriving criteria with asymptotic consistency results and an increasing emphasis on introducing non-asymptotic criteria. We focus on the problem of modeling non-linear relationships in regression data with potential hidden graph-structured interactions between the high-dimensional predictors, within the mixture of experts modeling framework. In order to deal with such a complex situation, we investigate a block-diagonal localized mixture of polynomial experts (BLoMPE) regression model, which is constructed upon an inverse regression and block-diagonal structures of the Gaussian expert covariance matrices. We introduce a penalized maximum likelihood selection criterion to estimate the unknown conditional density of the regression model. This model selection criterion allows us to handle the challenging problem of inferring the number of mixture components, the degree of polynomial mean functions, and the hidden block-diagonal structures of the covariance matrices, which reduces the number of parameters to be estimated and leads to a trade-off between complexity and sparsity in the model. In particular, we provide a strong theoretical guarantee: a finite-sample oracle inequality satisfied by the penalized maximum likelihood estimator with a Jensen-Kullback-Leibler type loss, to support the introduced non-asymptotic model selection criterion. The penalty shape of this criterion depends on the complexity of the considered random subcollection of BLoMPE models, including the relevant graph structures, the degree of polynomial mean functions, and the number of mixture components.

A non-asymptotic penalization criterion for model selection in mixture of experts models

Mixture of experts (MoE) is a popular class of models in statistics and machine learning that has sustained attention over the years, due to its flexibility and effectiveness. We consider the Gaussian-gated localized MoE (GLoME) regression model for modeling heterogeneous data. This model poses challenging questions with respect to the statistical estimation and model selection problems, including feature selection, both from the computational and theoretical points of view. We study the problem of estimating the number of components of the GLoME model, in a penalized maximum likelihood estimation framework. We provide a lower bound on the penalty that ensures a weak oracle inequality is satisfied by our estimator. To support our theoretical result, we perform numerical experiments on simulated and real data, which illustrate the performance of our finite-sample oracle inequality.

An $l_1$-oracle inequality for the Lasso in mixture-of-experts regression models

Mixture-of-experts (MoE) models are a popular framework for modeling heterogeneity in data, for both regression and classification problems in statistics and machine learning, due to their flexibility and the abundance of statistical estimation and model choice tools. Such flexibility comes from allowing the mixture weights (or gating functions) in the MoE model to depend on the explanatory variables, along with the experts (or component densities). This permits the modeling of data arising from more complex data generating processes, compared to the classical finite mixtures and finite mixtures of regression models, whose mixing parameters are independent of the covariates. The use of MoE models in a high-dimensional setting, when the number of explanatory variables can be much larger than the sample size (i.e., $p\gg n$), is challenging from a computational point of view, and in particular from a theoretical point of view, where the literature is still lacking results in dealing with the curse of dimensionality, in both the statistical estimation and feature selection. We consider the finite mixture-of-experts model with soft-max gating functions and Gaussian experts for high-dimensional regression on heterogeneous data, and its $l_1$-regularized estimation via the Lasso. We focus on the Lasso estimation properties rather than its feature selection properties. We provide a lower bound on the regularization parameter of the Lasso function that ensures an $l_1$-oracle inequality satisfied by the Lasso estimator according to the Kullback-Leibler loss.

Estimation and Feature Selection in Mixtures of Generalized Linear Experts Models

Mixtures-of-Experts (MoE) are conditional mixture models that have shown their performance in modeling heterogeneity in data in many statistical learning approaches for prediction, including regression and classification, as well as for clustering. Their estimation in high-dimensional problems is still however challenging. We consider the problem of parameter estimation and feature selection in MoE models with different generalized linear experts models, and propose a regularized maximum likelihood estimation that efficiently encourages sparse solutions for heterogeneous data with high-dimensional predictors. The developed proximal-Newton EM algorithm includes proximal Newton-type procedures to update the model parameter by monotonically maximizing the objective function and allows to perform efficient estimation and feature selection. An experimental study shows the good performance of the algorithms in terms of recovering the actual sparse solutions, parameter estimation, and clustering of heterogeneous regression data, compared to the main state-of-the art competitors.

Regularized Maximum Likelihood Estimation and Feature Selection in Mixtures-of-Experts Models

Mixture of Experts (MoE) are successful models for modeling heterogeneous data in many statistical learning problems including regression, clustering and classification. Generally fitted by maximum likelihood estimation via the well-known EM algorithm, their application to high-dimensional problems is still therefore challenging. We consider the problem of fitting and feature selection in MoE models, and propose a regularized maximum likelihood estimation approach that encourages sparse solutions for heterogeneous regression data models with potentially high-dimensional predictors. Unlike state-of-the art regularized MLE for MoE, the proposed modelings do not require an approximate of the penalty function. We develop two hybrid EM algorithms: an Expectation-Majorization-Maximization (EM/MM) algorithm, and an EM algorithm with coordinate ascent algorithm. The proposed algorithms allow to automatically obtaining sparse solutions without thresholding, and avoid matrix inversion by allowing univariate parameter updates. An experimental study shows the good performance of the algorithms in terms of recovering the actual sparse solutions, parameter estimation, and clustering of heterogeneous regression data.

Dirichlet Process Parsimonious Mixtures for clustering

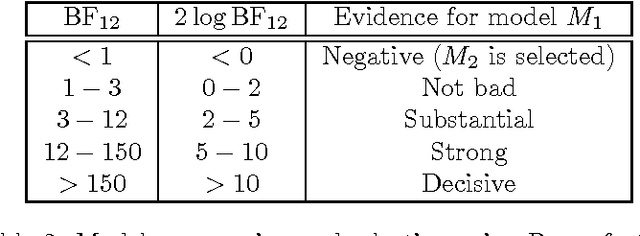
The parsimonious Gaussian mixture models, which exploit an eigenvalue decomposition of the group covariance matrices of the Gaussian mixture, have shown their success in particular in cluster analysis. Their estimation is in general performed by maximum likelihood estimation and has also been considered from a parametric Bayesian prospective. We propose new Dirichlet Process Parsimonious mixtures (DPPM) which represent a Bayesian nonparametric formulation of these parsimonious Gaussian mixture models. The proposed DPPM models are Bayesian nonparametric parsimonious mixture models that allow to simultaneously infer the model parameters, the optimal number of mixture components and the optimal parsimonious mixture structure from the data. We develop a Gibbs sampling technique for maximum a posteriori (MAP) estimation of the developed DPMM models and provide a Bayesian model selection framework by using Bayes factors. We apply them to cluster simulated data and real data sets, and compare them to the standard parsimonious mixture models. The obtained results highlight the effectiveness of the proposed nonparametric parsimonious mixture models as a good nonparametric alternative for the parametric parsimonious models.

Model-Based Clustering and Classification of Functional Data

The problem of complex data analysis is a central topic of modern statistical science and learning systems and is becoming of broader interest with the increasing prevalence of high-dimensional data. The challenge is to develop statistical models and autonomous algorithms that are able to acquire knowledge from raw data for exploratory analysis, which can be achieved through clustering techniques or to make predictions of future data via classification (i.e., discriminant analysis) techniques. Latent data models, including mixture model-based approaches are one of the most popular and successful approaches in both the unsupervised context (i.e., clustering) and the supervised one (i.e, classification or discrimination). Although traditionally tools of multivariate analysis, they are growing in popularity when considered in the framework of functional data analysis (FDA). FDA is the data analysis paradigm in which the individual data units are functions (e.g., curves, surfaces), rather than simple vectors. In many areas of application, the analyzed data are indeed often available in the form of discretized values of functions or curves (e.g., time series, waveforms) and surfaces (e.g., 2d-images, spatio-temporal data). This functional aspect of the data adds additional difficulties compared to the case of a classical multivariate (non-functional) data analysis. We review and present approaches for model-based clustering and classification of functional data. We derive well-established statistical models along with efficient algorithmic tools to address problems regarding the clustering and the classification of these high-dimensional data, including their heterogeneity, missing information, and dynamical hidden structure. The presented models and algorithms are illustrated on real-world functional data analysis problems from several application area.

An Introduction to the Practical and Theoretical Aspects of Mixture-of-Experts Modeling

Mixture-of-experts (MoE) models are a powerful paradigm for modeling of data arising from complex data generating processes (DGPs). In this article, we demonstrate how different MoE models can be constructed to approximate the underlying DGPs of arbitrary types of data. Due to the probabilistic nature of MoE models, we propose the maximum quasi-likelihood (MQL) estimator as a method for estimating MoE model parameters from data, and we provide conditions under which MQL estimators are consistent and asymptotically normal. The blockwise minorization-maximizatoin (blockwise-MM) algorithm framework is proposed as an all-purpose method for constructing algorithms for obtaining MQL estimators. An example derivation of a blockwise-MM algorithm is provided. We then present a method for constructing information criteria for estimating the number of components in MoE models and provide justification for the classic Bayesian information criterion (BIC). We explain how MoE models can be used to conduct classification, clustering, and regression and we illustrate these applications via a pair of worked examples.