A DNN Framework for Learning Lagrangian Drift With Uncertainty

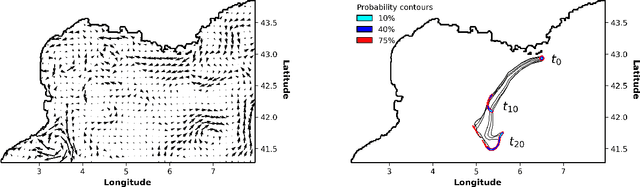
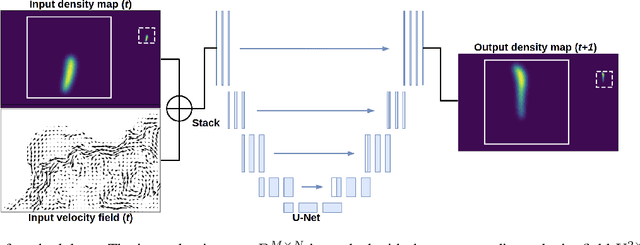
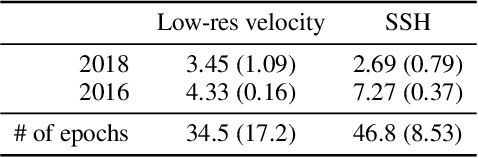
Reconstructions of Lagrangian drift, for example for objects lost at sea, are often uncertain due to unresolved physical phenomena within the data. Uncertainty is usually overcome by introducing stochasticity into the drift, but this approach requires specific assumptions for modelling uncertainty. We remove this constraint by presenting a purely data-driven framework for modelling probabilistic drift in flexible environments. We train a CNN to predict the temporal evolution of probability density maps of particle locations from $t$ to $t+1$ given an input velocity field. We generate groundtruth density maps on the basis of ocean circulation model simulations by simulating uncertainty in the initial position of particle trajectories. Several loss functions for regressing the predicted density maps are tested. Through evaluating our model on unseen velocities from a different year, we find its outputs to be in good agreement with numerical simulations, suggesting satisfactory generalisation to different dynamical situations.

The bioacoustic proof of the effects of raising awareness of noise pollution among visitors to the Port Cros National Park using binding communication

Assuming that the anthropogenic impact of visitors to a natural park can be reduced by communication actions, we have drawn up a bioacoustical protocol combined with a protocol to measure the effectiveness of the communication actions. A simple eco-awareness communication method will be compared to a binding communication method. We address the questions: does visitors' eco-awareness drive them to change their attitudes and behavior in order to limit their own noise disturbance, and does commitment improve their awareness? We detail here the main concepts considered and the methodology followed to discuss the preliminary results.

Dirichlet Process Parsimonious Mixtures for clustering

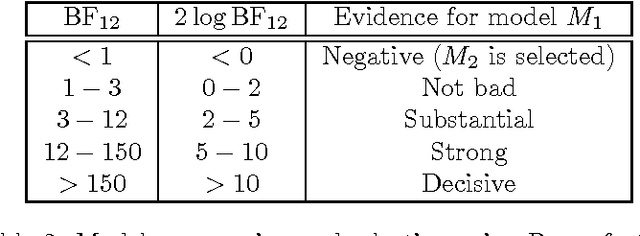
The parsimonious Gaussian mixture models, which exploit an eigenvalue decomposition of the group covariance matrices of the Gaussian mixture, have shown their success in particular in cluster analysis. Their estimation is in general performed by maximum likelihood estimation and has also been considered from a parametric Bayesian prospective. We propose new Dirichlet Process Parsimonious mixtures (DPPM) which represent a Bayesian nonparametric formulation of these parsimonious Gaussian mixture models. The proposed DPPM models are Bayesian nonparametric parsimonious mixture models that allow to simultaneously infer the model parameters, the optimal number of mixture components and the optimal parsimonious mixture structure from the data. We develop a Gibbs sampling technique for maximum a posteriori (MAP) estimation of the developed DPMM models and provide a Bayesian model selection framework by using Bayes factors. We apply them to cluster simulated data and real data sets, and compare them to the standard parsimonious mixture models. The obtained results highlight the effectiveness of the proposed nonparametric parsimonious mixture models as a good nonparametric alternative for the parametric parsimonious models.

Mixture model-based functional discriminant analysis for curve classification

Statistical approaches for Functional Data Analysis concern the paradigm for which the individuals are functions or curves rather than finite dimensional vectors. In this paper, we particularly focus on the modeling and the classification of functional data which are temporal curves presenting regime changes over time. More specifically, we propose a new mixture model-based discriminant analysis approach for functional data using a specific hidden process regression model. Our approach is particularly adapted to both handle the problem of complex-shaped classes of curves, where each class is composed of several sub-classes, and to deal with the regime changes within each homogeneous sub-class. The model explicitly integrates the heterogeneity of each class of curves via a mixture model formulation, and the regime changes within each sub-class through a hidden logistic process. The approach allows therefore for fitting flexible curve-models to each class of complex-shaped curves presenting regime changes through an unsupervised learning scheme, to automatically summarize it into a finite number of homogeneous clusters, each of them is decomposed into several regimes. The model parameters are learned by maximizing the observed-data log-likelihood for each class by using a dedicated expectation-maximization (EM) algorithm. Comparisons on simulated data and real data with alternative approaches, including functional linear discriminant analysis and functional mixture discriminant analysis with polynomial regression mixtures and spline regression mixtures, show that the proposed approach provides better results regarding the discrimination results and significantly improves the curves approximation.

Model-based functional mixture discriminant analysis with hidden process regression for curve classification

In this paper, we study the modeling and the classification of functional data presenting regime changes over time. We propose a new model-based functional mixture discriminant analysis approach based on a specific hidden process regression model that governs the regime changes over time. Our approach is particularly adapted to handle the problem of complex-shaped classes of curves, where each class is potentially composed of several sub-classes, and to deal with the regime changes within each homogeneous sub-class. The proposed model explicitly integrates the heterogeneity of each class of curves via a mixture model formulation, and the regime changes within each sub-class through a hidden logistic process. Each class of complex-shaped curves is modeled by a finite number of homogeneous clusters, each of them being decomposed into several regimes. The model parameters of each class are learned by maximizing the observed-data log-likelihood by using a dedicated expectation-maximization (EM) algorithm. Comparisons are performed with alternative curve classification approaches, including functional linear discriminant analysis and functional mixture discriminant analysis with polynomial regression mixtures and spline regression mixtures. Results obtained on simulated data and real data show that the proposed approach outperforms the alternative approaches in terms of discrimination, and significantly improves the curves approximation.

Physeter catodon localization by sparse coding

This paper presents a spermwhale' localization architecture using jointly a bag-of-features (BoF) approach and machine learning framework. BoF methods are known, especially in computer vision, to produce from a collection of local features a global representation invariant to principal signal transformations. Our idea is to regress supervisely from these local features two rough estimates of the distance and azimuth thanks to some datasets where both acoustic events and ground-truth position are now available. Furthermore, these estimates can feed a particle filter system in order to obtain a precise spermwhale' position even in mono-hydrophone configuration. Anti-collision system and whale watching are considered applications of this work.

Stochastic Low-Rank Kernel Learning for Regression

We present a novel approach to learn a kernel-based regression function. It is based on the useof conical combinations of data-based parameterized kernels and on a new stochastic convex optimization procedure of which we establish convergence guarantees. The overall learning procedure has the nice properties that a) the learned conical combination is automatically designed to perform the regression task at hand and b) the updates implicated by the optimization procedure are quite inexpensive. In order to shed light on the appositeness of our learning strategy, we present empirical results from experiments conducted on various benchmark datasets.