A DNN Framework for Learning Lagrangian Drift With Uncertainty

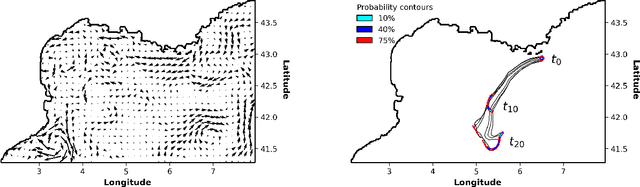
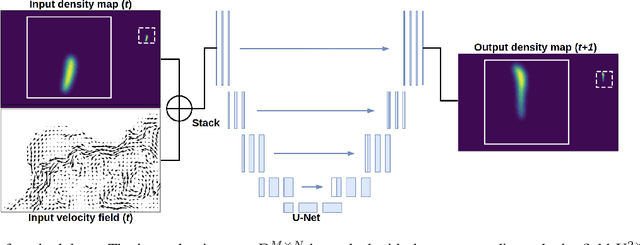
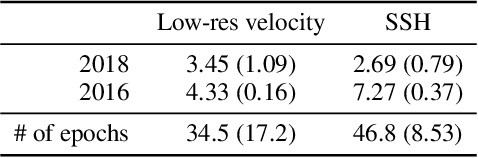
Reconstructions of Lagrangian drift, for example for objects lost at sea, are often uncertain due to unresolved physical phenomena within the data. Uncertainty is usually overcome by introducing stochasticity into the drift, but this approach requires specific assumptions for modelling uncertainty. We remove this constraint by presenting a purely data-driven framework for modelling probabilistic drift in flexible environments. We train a CNN to predict the temporal evolution of probability density maps of particle locations from $t$ to $t+1$ given an input velocity field. We generate groundtruth density maps on the basis of ocean circulation model simulations by simulating uncertainty in the initial position of particle trajectories. Several loss functions for regressing the predicted density maps are tested. Through evaluating our model on unseen velocities from a different year, we find its outputs to be in good agreement with numerical simulations, suggesting satisfactory generalisation to different dynamical situations.