A Regression Mixture Model to understand the effect of the Covid-19 pandemic on Public Transport Ridership

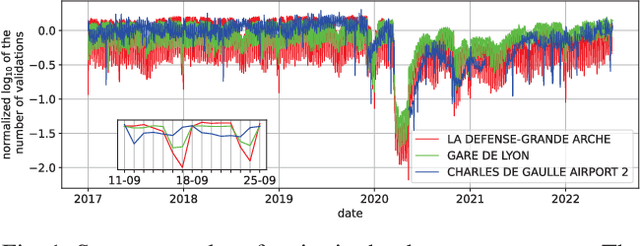
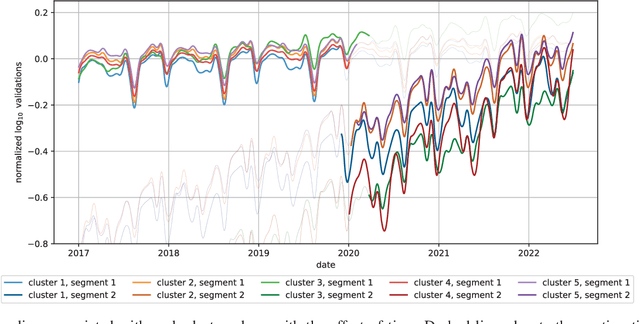
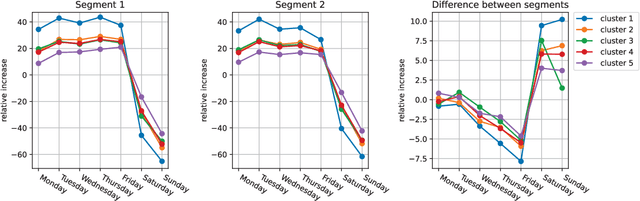
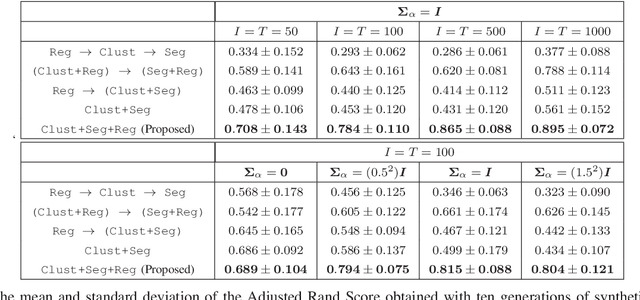
The Covid-19 pandemic drastically changed urban mobility, both during the height of the pandemic with government lockdowns, but also in the longer term with the adoption of working-from-home policies. To understand its effects on rail public transport ridership, we propose a dedicated Regression Mixture Model able to perform both the clustering of public transport stations and the segmentation of time periods, while ignoring variations due to additional variables such as the official lockdowns or non-working days. Each cluster is thus defined by a series of segments in which the effect of the exogenous variables is constant. As each segment within a cluster has its own regression coefficients to model the impact of the covariates, we analyze how these coefficients evolve to understand the changes in the cluster. We present the regression mixture model and the parameter estimation using the EM algorithm, before demonstrating the benefits of the model on both simulated and real data. Thanks to a five-year dataset of the ridership in the Paris public transport system, we analyze the impact of the pandemic, not only in terms of the number of travelers but also on the weekly commute. We further analyze the specific changes that the pandemic caused inside each cluster.

Model-based clustering with Hidden Markov Model regression for time series with regime changes

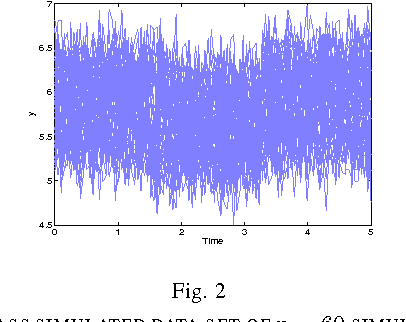
This paper introduces a novel model-based clustering approach for clustering time series which present changes in regime. It consists of a mixture of polynomial regressions governed by hidden Markov chains. The underlying hidden process for each cluster activates successively several polynomial regimes during time. The parameter estimation is performed by the maximum likelihood method through a dedicated Expectation-Maximization (EM) algorithm. The proposed approach is evaluated using simulated time series and real-world time series issued from a railway diagnosis application. Comparisons with existing approaches for time series clustering, including the stand EM for Gaussian mixtures, $K$-means clustering, the standard mixture of regression models and mixture of Hidden Markov Models, demonstrate the effectiveness of the proposed approach.

Classification automatique de données temporelles en classes ordonnées

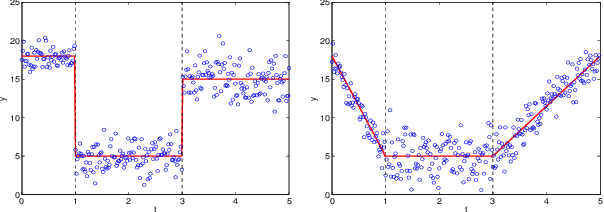
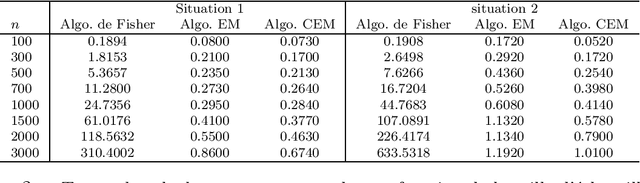
This paper proposes a method of segmenting temporal data into ordered classes. It is based on mixture models and a discrete latent process, which enables to successively activates the classes. The classification can be performed by maximizing the likelihood via the EM algorithm or by simultaneously optimizing the model parameters and the partition by the CEM algorithm. These two algorithms can be seen as alternatives to Fisher's algorithm, which improve its computing time.

A regression model with a hidden logistic process for feature extraction from time series

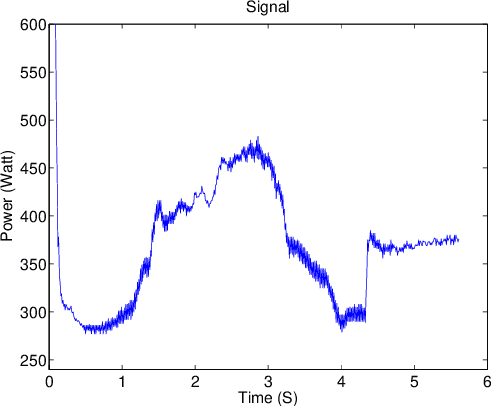
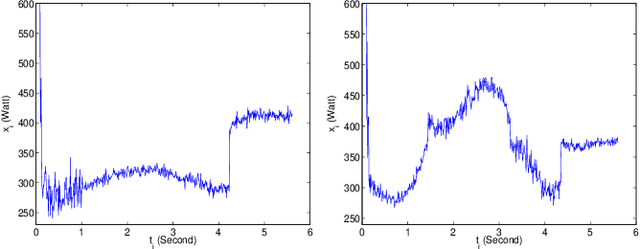
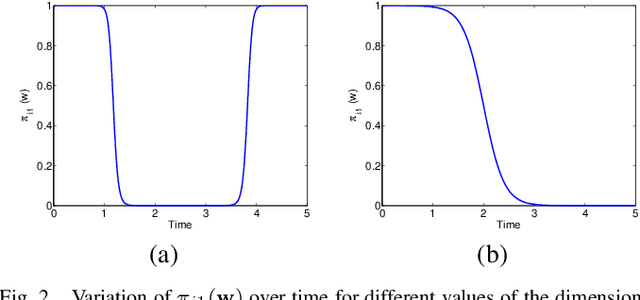
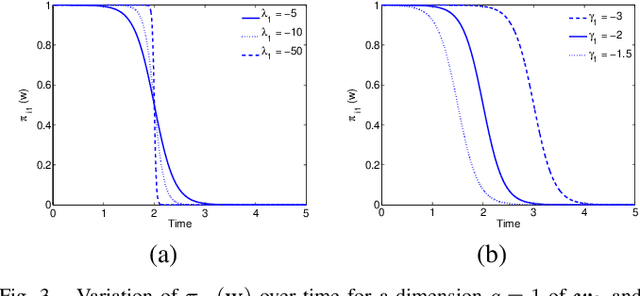
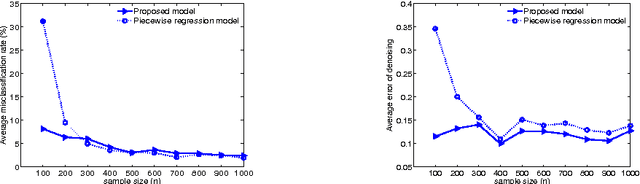
A new approach for feature extraction from time series is proposed in this paper. This approach consists of a specific regression model incorporating a discrete hidden logistic process. The model parameters are estimated by the maximum likelihood method performed by a dedicated Expectation Maximization (EM) algorithm. The parameters of the hidden logistic process, in the inner loop of the EM algorithm, are estimated using a multi-class Iterative Reweighted Least-Squares (IRLS) algorithm. A piecewise regression algorithm and its iterative variant have also been considered for comparisons. An experimental study using simulated and real data reveals good performances of the proposed approach.

A regression model with a hidden logistic process for signal parametrization

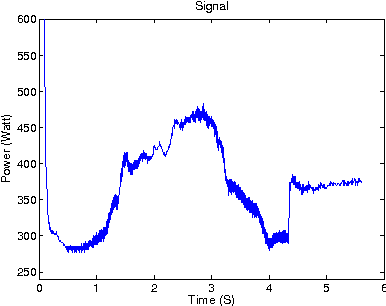
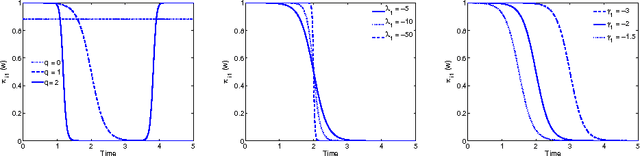
A new approach for signal parametrization, which consists of a specific regression model incorporating a discrete hidden logistic process, is proposed. The model parameters are estimated by the maximum likelihood method performed by a dedicated Expectation Maximization (EM) algorithm. The parameters of the hidden logistic process, in the inner loop of the EM algorithm, are estimated using a multi-class Iterative Reweighted Least-Squares (IRLS) algorithm. An experimental study using simulated and real data reveals good performances of the proposed approach.

Modèle à processus latent et algorithme EM pour la régression non linéaire

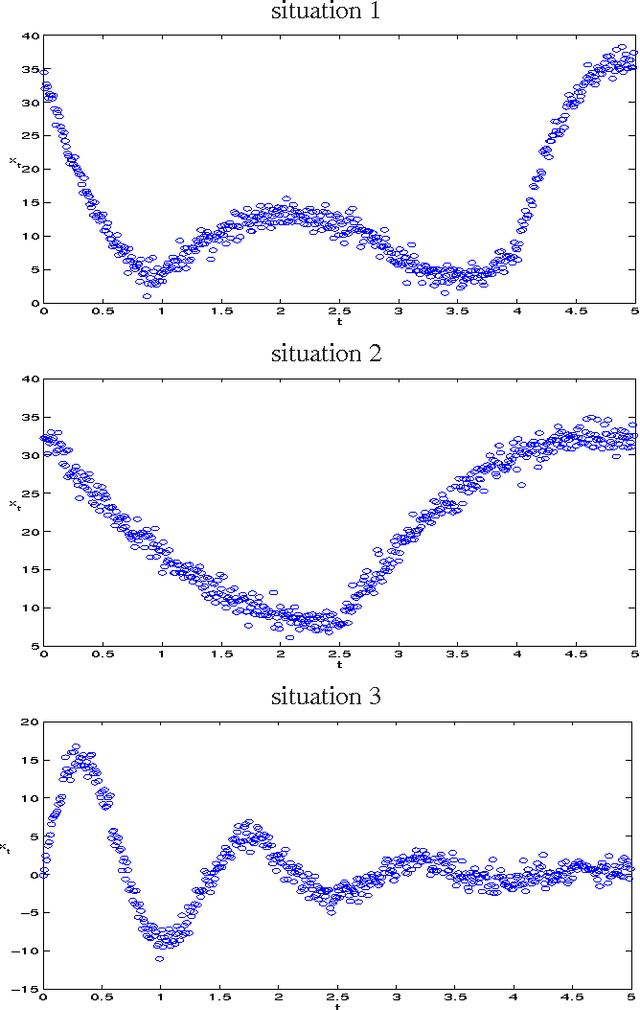
A non linear regression approach which consists of a specific regression model incorporating a latent process, allowing various polynomial regression models to be activated preferentially and smoothly, is introduced in this paper. The model parameters are estimated by maximum likelihood performed via a dedicated expecation-maximization (EM) algorithm. An experimental study using simulated and real data sets reveals good performances of the proposed approach.

Time series modeling by a regression approach based on a latent process

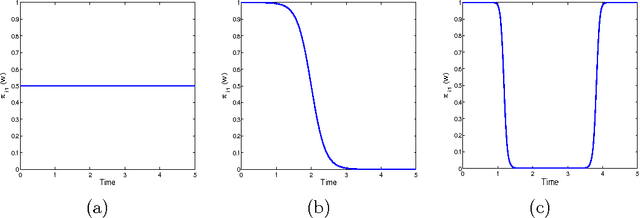
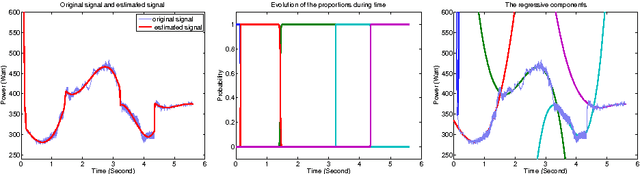
Time series are used in many domains including finance, engineering, economics and bioinformatics generally to represent the change of a measurement over time. Modeling techniques may then be used to give a synthetic representation of such data. A new approach for time series modeling is proposed in this paper. It consists of a regression model incorporating a discrete hidden logistic process allowing for activating smoothly or abruptly different polynomial regression models. The model parameters are estimated by the maximum likelihood method performed by a dedicated Expectation Maximization (EM) algorithm. The M step of the EM algorithm uses a multi-class Iterative Reweighted Least-Squares (IRLS) algorithm to estimate the hidden process parameters. To evaluate the proposed approach, an experimental study on simulated data and real world data was performed using two alternative approaches: a heteroskedastic piecewise regression model using a global optimization algorithm based on dynamic programming, and a Hidden Markov Regression Model whose parameters are estimated by the Baum-Welch algorithm. Finally, in the context of the remote monitoring of components of the French railway infrastructure, and more particularly the switch mechanism, the proposed approach has been applied to modeling and classifying time series representing the condition measurements acquired during switch operations.

A hidden process regression model for functional data description. Application to curve discrimination

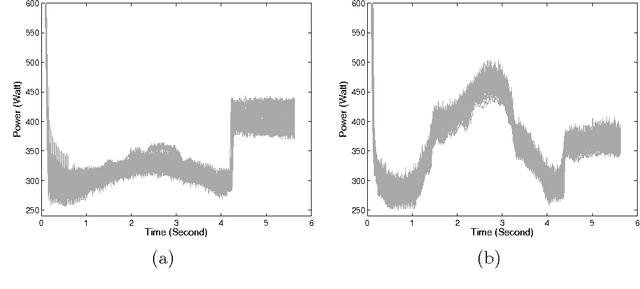
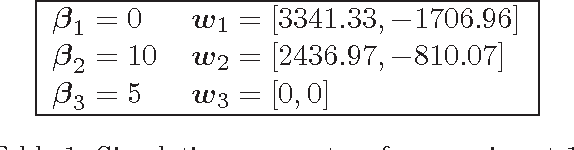
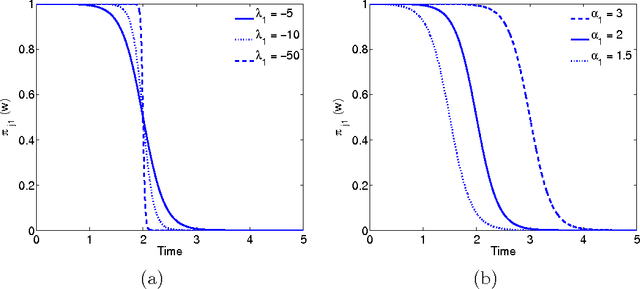
A new approach for functional data description is proposed in this paper. It consists of a regression model with a discrete hidden logistic process which is adapted for modeling curves with abrupt or smooth regime changes. The model parameters are estimated in a maximum likelihood framework through a dedicated Expectation Maximization (EM) algorithm. From the proposed generative model, a curve discrimination rule is derived using the Maximum A Posteriori rule. The proposed model is evaluated using simulated curves and real world curves acquired during railway switch operations, by performing comparisons with the piecewise regression approach in terms of curve modeling and classification.

Model-based clustering and segmentation of time series with changes in regime

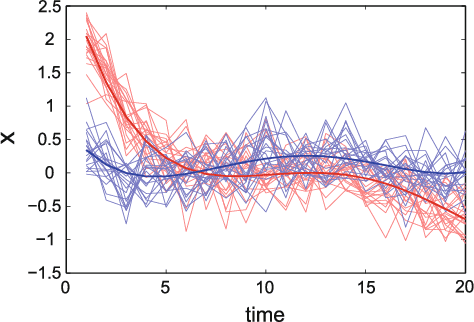
Mixture model-based clustering, usually applied to multidimensional data, has become a popular approach in many data analysis problems, both for its good statistical properties and for the simplicity of implementation of the Expectation-Maximization (EM) algorithm. Within the context of a railway application, this paper introduces a novel mixture model for dealing with time series that are subject to changes in regime. The proposed approach consists in modeling each cluster by a regression model in which the polynomial coefficients vary according to a discrete hidden process. In particular, this approach makes use of logistic functions to model the (smooth or abrupt) transitions between regimes. The model parameters are estimated by the maximum likelihood method solved by an Expectation-Maximization algorithm. The proposed approach can also be regarded as a clustering approach which operates by finding groups of time series having common changes in regime. In addition to providing a time series partition, it therefore provides a time series segmentation. The problem of selecting the optimal numbers of clusters and segments is solved by means of the Bayesian Information Criterion (BIC). The proposed approach is shown to be efficient using a variety of simulated time series and real-world time series of electrical power consumption from rail switching operations.

Model-based functional mixture discriminant analysis with hidden process regression for curve classification

In this paper, we study the modeling and the classification of functional data presenting regime changes over time. We propose a new model-based functional mixture discriminant analysis approach based on a specific hidden process regression model that governs the regime changes over time. Our approach is particularly adapted to handle the problem of complex-shaped classes of curves, where each class is potentially composed of several sub-classes, and to deal with the regime changes within each homogeneous sub-class. The proposed model explicitly integrates the heterogeneity of each class of curves via a mixture model formulation, and the regime changes within each sub-class through a hidden logistic process. Each class of complex-shaped curves is modeled by a finite number of homogeneous clusters, each of them being decomposed into several regimes. The model parameters of each class are learned by maximizing the observed-data log-likelihood by using a dedicated expectation-maximization (EM) algorithm. Comparisons are performed with alternative curve classification approaches, including functional linear discriminant analysis and functional mixture discriminant analysis with polynomial regression mixtures and spline regression mixtures. Results obtained on simulated data and real data show that the proposed approach outperforms the alternative approaches in terms of discrimination, and significantly improves the curves approximation.