AICov: An Integrative Deep Learning Framework for COVID-19 Forecasting with Population Covariates

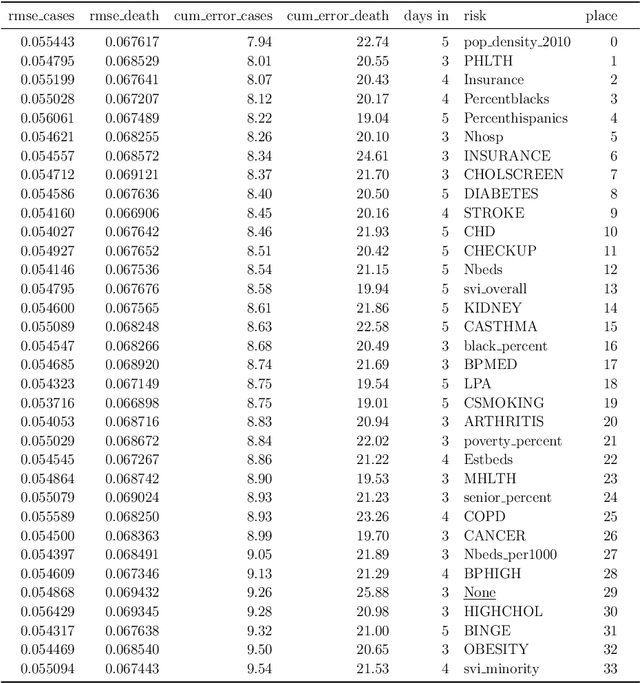
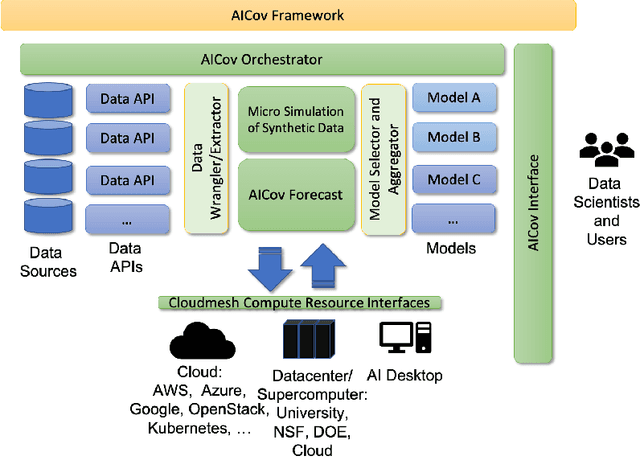
The COVID-19 pandemic has profound global consequences on health, economic, social, political, and almost every major aspect of human life. Therefore, it is of great importance to model COVID-19 and other pandemics in terms of the broader social contexts in which they take place. We present the architecture of AICov, which provides an integrative deep learning framework for COVID-19 forecasting with population covariates, some of which may serve as putative risk factors. We have integrated multiple different strategies into AICov, including the ability to use deep learning strategies based on LSTM and even modeling. To demonstrate our approach, we have conducted a pilot that integrates population covariates from multiple sources. Thus, AICov not only includes data on COVID-19 cases and deaths but, more importantly, the population's socioeconomic, health and behavioral risk factors at a local level. The compiled data are fed into AICov, and thus we obtain improved prediction by integration of the data to our model as compared to one that only uses case and death data.

Supervised Classification of Flow Cytometric Samples via the Joint Clustering and Matching (JCM) Procedure

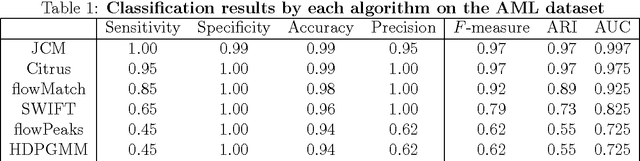
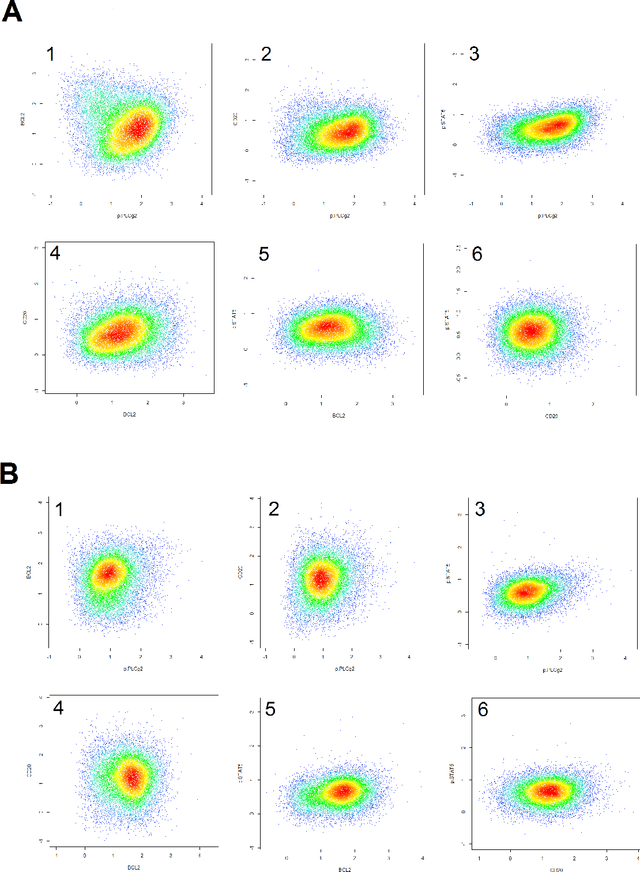
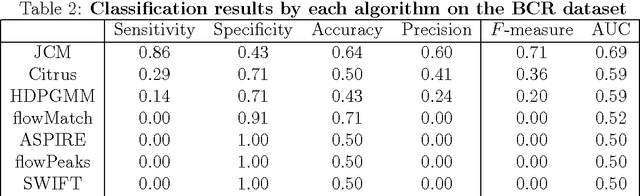
We consider the use of the Joint Clustering and Matching (JCM) procedure for the supervised classification of a flow cytometric sample with respect to a number of predefined classes of such samples. The JCM procedure has been proposed as a method for the unsupervised classification of cells within a sample into a number of clusters and in the case of multiple samples, the matching of these clusters across the samples. The two tasks of clustering and matching of the clusters are performed simultaneously within the JCM framework. In this paper, we consider the case where there is a number of distinct classes of samples whose class of origin is known, and the problem is to classify a new sample of unknown class of origin to one of these predefined classes. For example, the different classes might correspond to the types of a particular disease or to the various health outcomes of a patient subsequent to a course of treatment. We show and demonstrate on some real datasets how the JCM procedure can be used to carry out this supervised classification task. A mixture distribution is used to model the distribution of the expressions of a fixed set of markers for each cell in a sample with the components in the mixture model corresponding to the various populations of cells in the composition of the sample. For each class of samples, a class template is formed by the adoption of random-effects terms to model the inter-sample variation within a class. The classification of a new unclassified sample is undertaken by assigning the unclassified sample to the class that minimizes the Kullback-Leibler distance between its fitted mixture density and each class density provided by the class templates.

Joint Modeling and Registration of Cell Populations in Cohorts of High-Dimensional Flow Cytometric Data

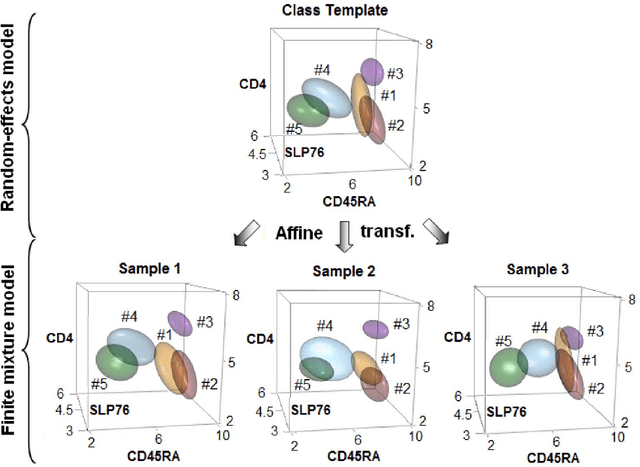
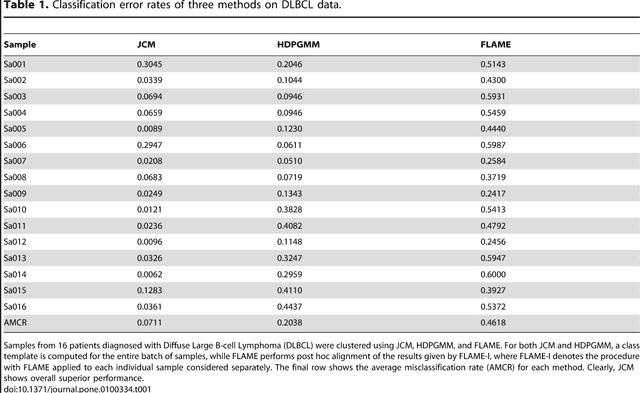
In systems biomedicine, an experimenter encounters different potential sources of variation in data such as individual samples, multiple experimental conditions, and multi-variable network-level responses. In multiparametric cytometry, which is often used for analyzing patient samples, such issues are critical. While computational methods can identify cell populations in individual samples, without the ability to automatically match them across samples, it is difficult to compare and characterize the populations in typical experiments, such as those responding to various stimulations or distinctive of particular patients or time-points, especially when there are many samples. Joint Clustering and Matching (JCM) is a multi-level framework for simultaneous modeling and registration of populations across a cohort. JCM models every population with a robust multivariate probability distribution. Simultaneously, JCM fits a random-effects model to construct an overall batch template -- used for registering populations across samples, and classifying new samples. By tackling systems-level variation, JCM supports practical biomedical applications involving large cohorts.