Nearest Neighbor Median Shift Clustering for Binary Data

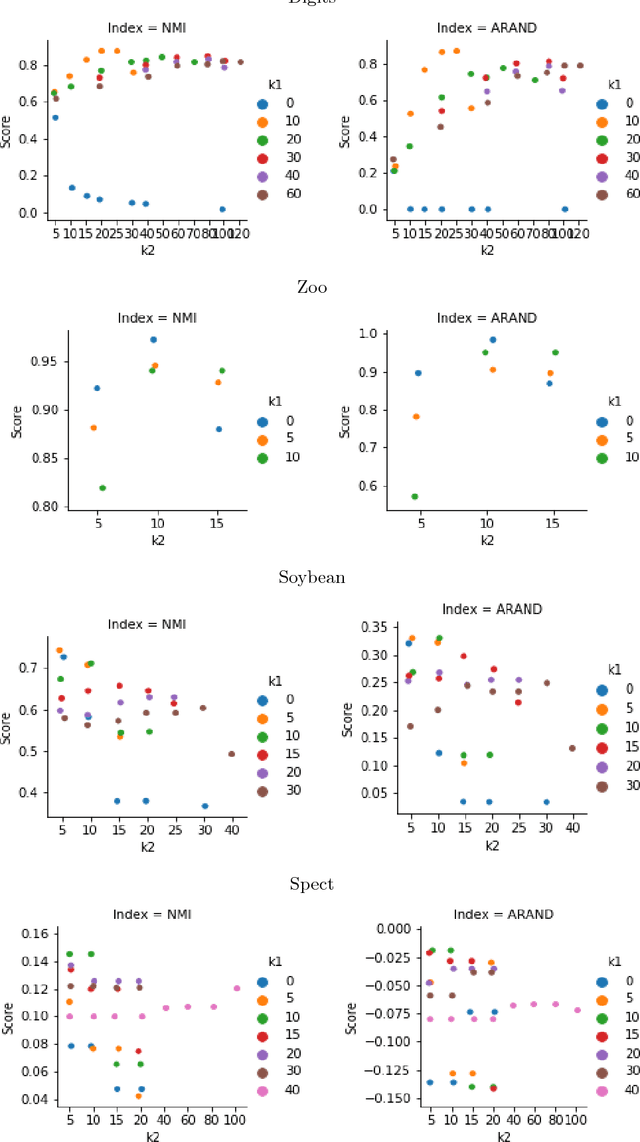
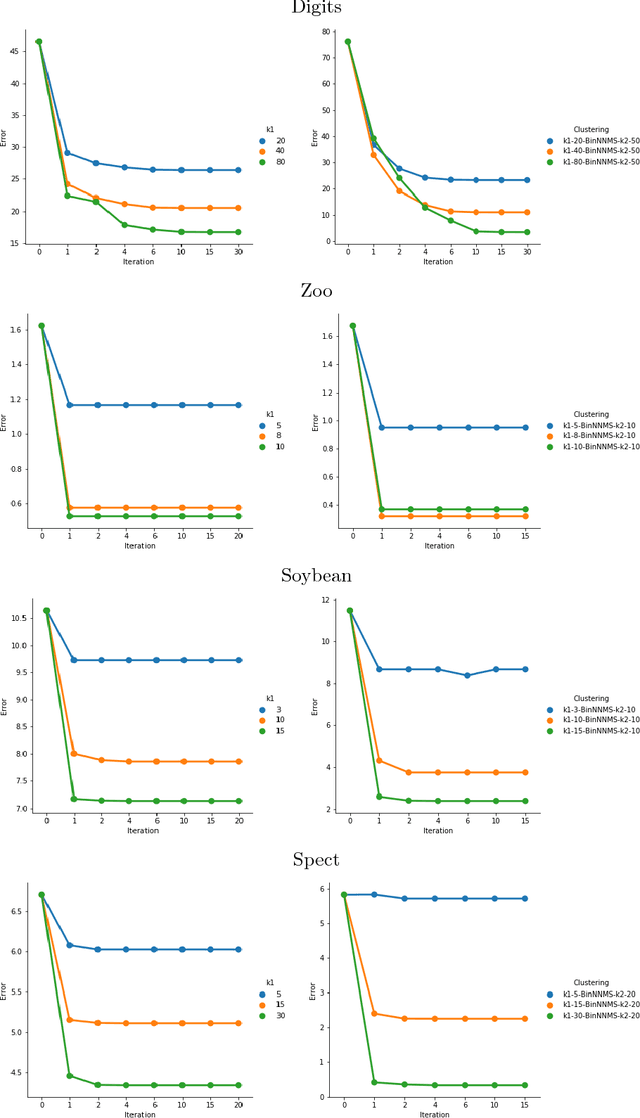
We describe in this paper the theory and practice behind a new modal clustering method for binary data. Our approach (BinNNMS) is based on the nearest neighbor median shift. The median shift is an extension of the well-known mean shift, which was designed for continuous data, to handle binary data. We demonstrate that BinNNMS can discover accurately the location of clusters in binary data with theoretical and experimental analyses.

A Distributed and Approximated Nearest Neighbors Algorithm for an Efficient Large Scale Mean Shift Clustering

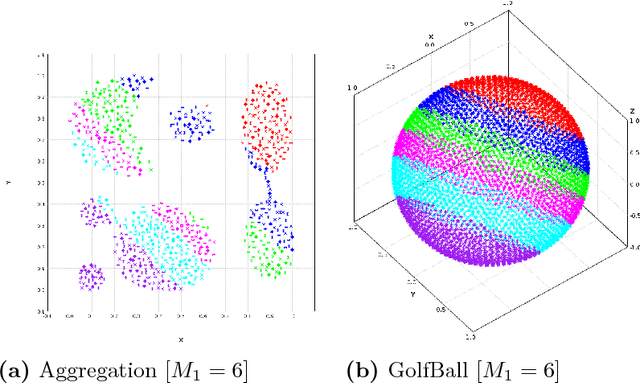
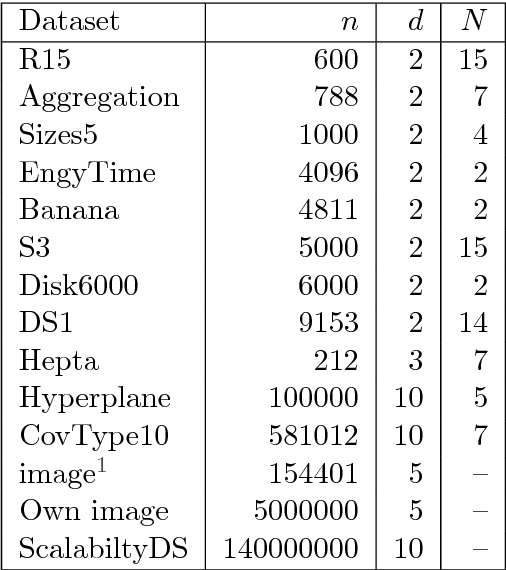
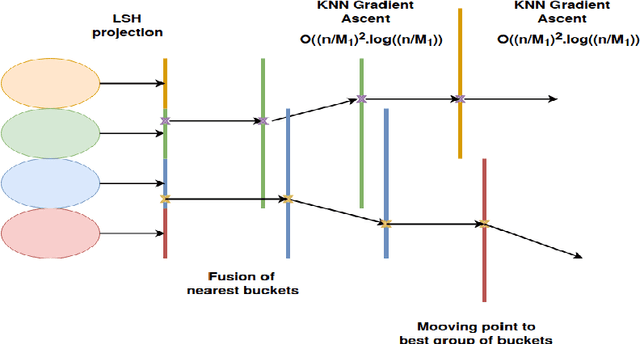
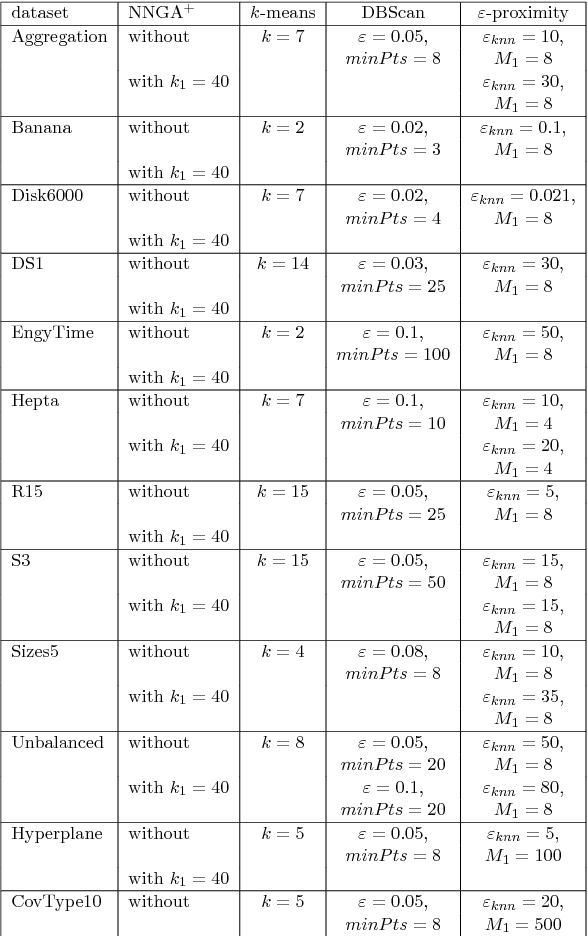
In this paper we target the class of modal clustering methods where clusters are defined in terms of the local modes of the probability density function which generates the data. The most well-known modal clustering method is the k-means clustering. Mean Shift clustering is a generalization of the k-means clustering which computes arbitrarily shaped clusters as defined as the basins of attraction to the local modes created by the density gradient ascent paths. Despite its potential, the Mean Shift approach is a computationally expensive method for unsupervised learning. Thus, we introduce two contributions aiming to provide clustering algorithms with a linear time complexity, as opposed to the quadratic time complexity for the exact Mean Shift clustering. Firstly we propose a scalable procedure to approximate the density gradient ascent. Second, our proposed scalable cluster labeling technique is presented. Both propositions are based on Locality Sensitive Hashing (LSH) to approximate nearest neighbors. These two techniques may be used for moderate sized datasets. Furthermore, we show that using our proposed approximations of the density gradient ascent as a pre-processing step in other clustering methods can also improve dedicated classification metrics. For the latter, a distributed implementation, written for the Spark/Scala ecosystem is proposed. For all these considered clustering methods, we present experimental results illustrating their labeling accuracy and their potential to solve concrete problems.

Joint Modeling and Registration of Cell Populations in Cohorts of High-Dimensional Flow Cytometric Data

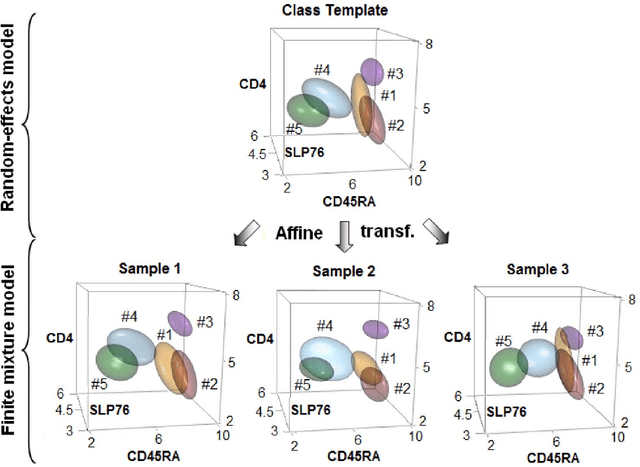
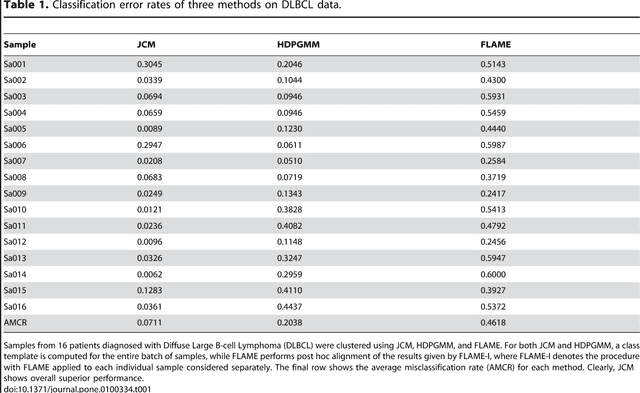
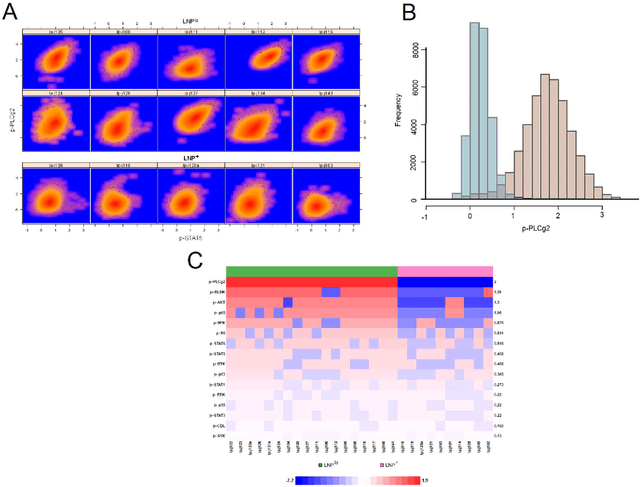
In systems biomedicine, an experimenter encounters different potential sources of variation in data such as individual samples, multiple experimental conditions, and multi-variable network-level responses. In multiparametric cytometry, which is often used for analyzing patient samples, such issues are critical. While computational methods can identify cell populations in individual samples, without the ability to automatically match them across samples, it is difficult to compare and characterize the populations in typical experiments, such as those responding to various stimulations or distinctive of particular patients or time-points, especially when there are many samples. Joint Clustering and Matching (JCM) is a multi-level framework for simultaneous modeling and registration of populations across a cohort. JCM models every population with a robust multivariate probability distribution. Simultaneously, JCM fits a random-effects model to construct an overall batch template -- used for registering populations across samples, and classifying new samples. By tackling systems-level variation, JCM supports practical biomedical applications involving large cohorts.

Data-driven density derivative estimation, with applications to nonparametric clustering and bump hunting

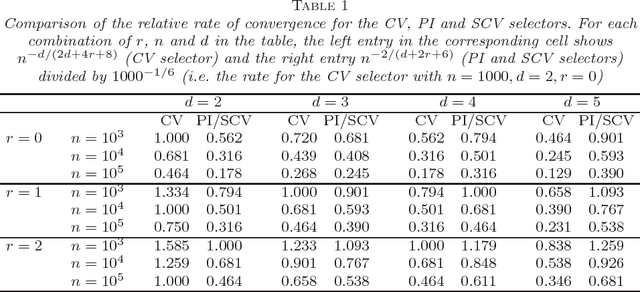
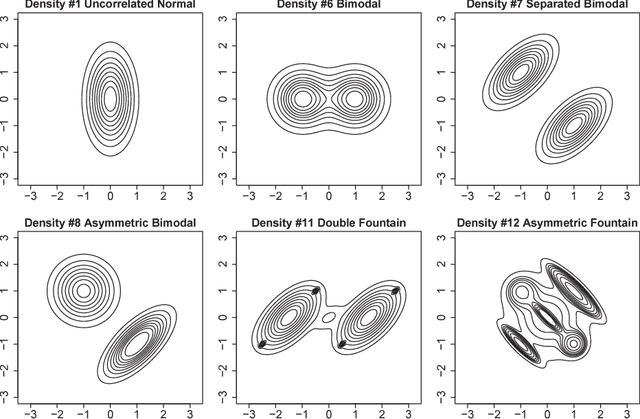
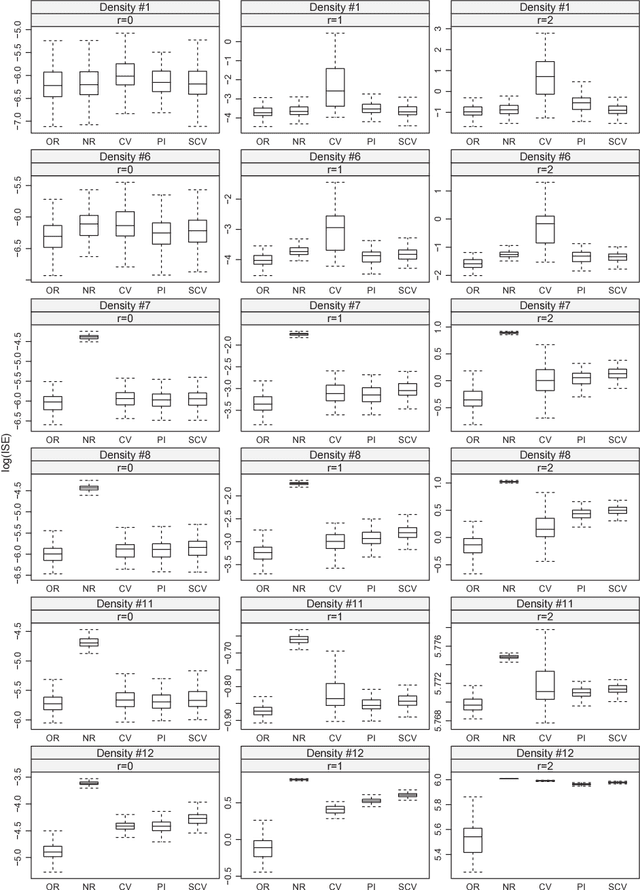
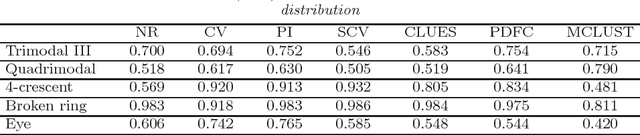
Important information concerning a multivariate data set, such as clusters and modal regions, is contained in the derivatives of the probability density function. Despite this importance, nonparametric estimation of higher order derivatives of the density functions have received only relatively scant attention. Kernel estimators of density functions are widely used as they exhibit excellent theoretical and practical properties, though their generalization to density derivatives has progressed more slowly due to the mathematical intractabilities encountered in the crucial problem of bandwidth (or smoothing parameter) selection. This paper presents the first fully automatic, data-based bandwidth selectors for multivariate kernel density derivative estimators. This is achieved by synthesizing recent advances in matrix analytic theory which allow mathematically and computationally tractable representations of higher order derivatives of multivariate vector valued functions. The theoretical asymptotic properties as well as the finite sample behaviour of the proposed selectors are studied. {In addition, we explore in detail the applications of the new data-driven methods for two other statistical problems: clustering and bump hunting. The introduced techniques are combined with the mean shift algorithm to develop novel automatic, nonparametric clustering procedures which are shown to outperform mixture-model cluster analysis and other recent nonparametric approaches in practice. Furthermore, the advantage of the use of smoothing parameters designed for density derivative estimation for feature significance analysis for bump hunting is illustrated with a real data example.