Algorithms for an Efficient Tensor Biclustering

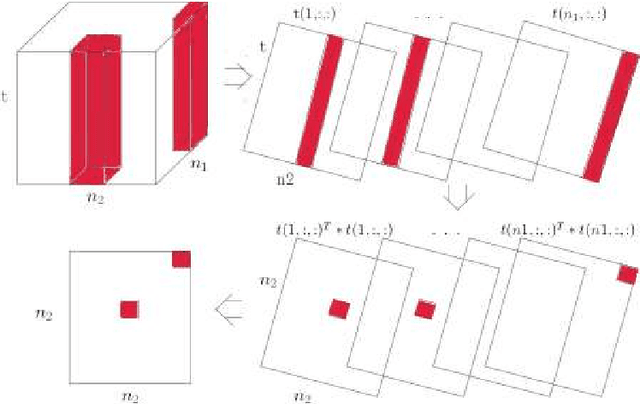
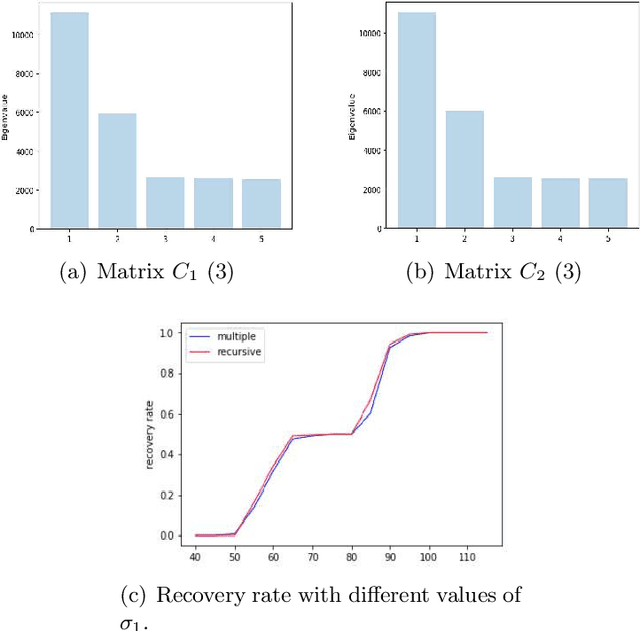
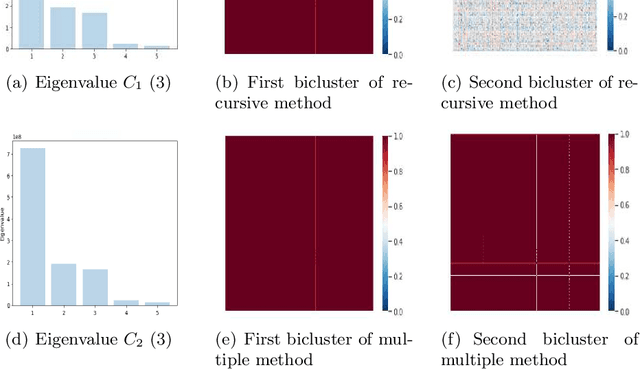
Consider a data set collected by (individuals-features) pairs in different times. It can be represented as a tensor of three dimensions (Individuals, features and times). The tensor biclustering problem computes a subset of individuals and a subset of features whose signal trajectories over time lie in a low-dimensional subspace, modeling similarity among the signal trajectories while allowing different scalings across different individuals or different features. This approach are based on spectral decomposition in order to build the desired biclusters. We evaluate the quality of the results from each algorithms with both synthetic and real data set.

Nearest Neighbor Median Shift Clustering for Binary Data

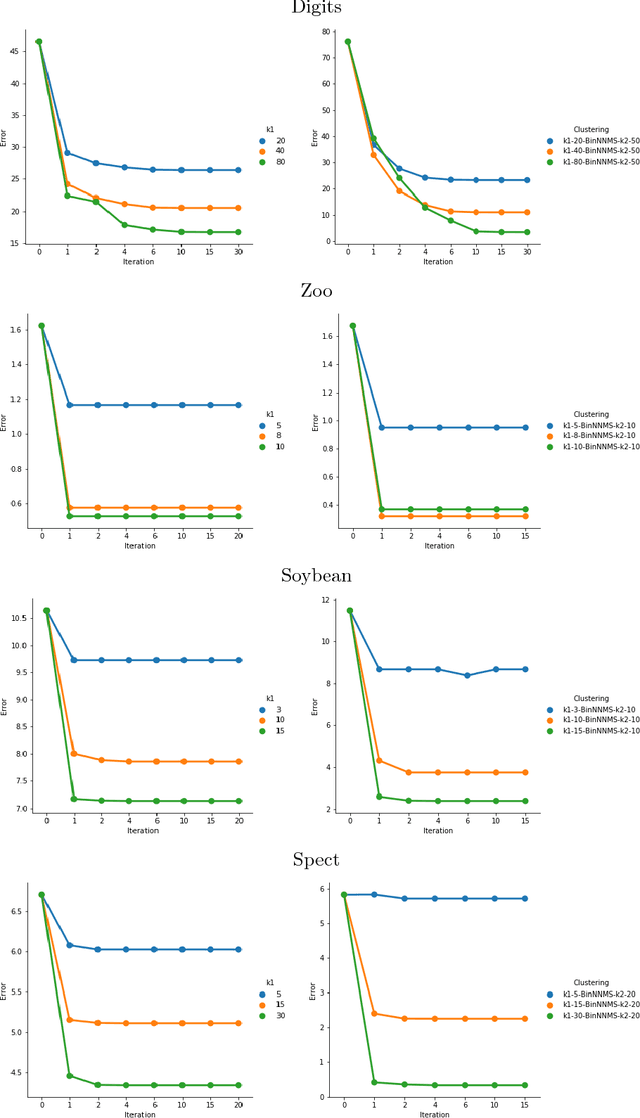
We describe in this paper the theory and practice behind a new modal clustering method for binary data. Our approach (BinNNMS) is based on the nearest neighbor median shift. The median shift is an extension of the well-known mean shift, which was designed for continuous data, to handle binary data. We demonstrate that BinNNMS can discover accurately the location of clusters in binary data with theoretical and experimental analyses.

A Distributed and Approximated Nearest Neighbors Algorithm for an Efficient Large Scale Mean Shift Clustering

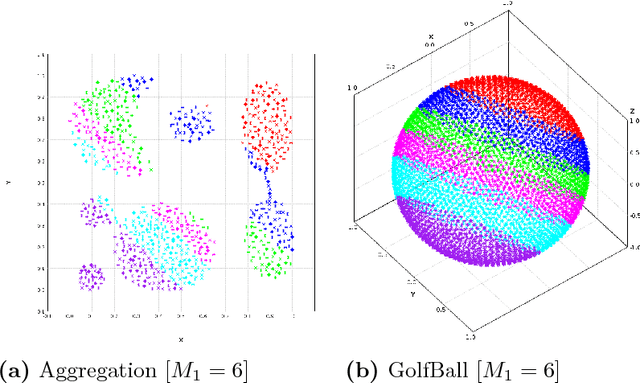
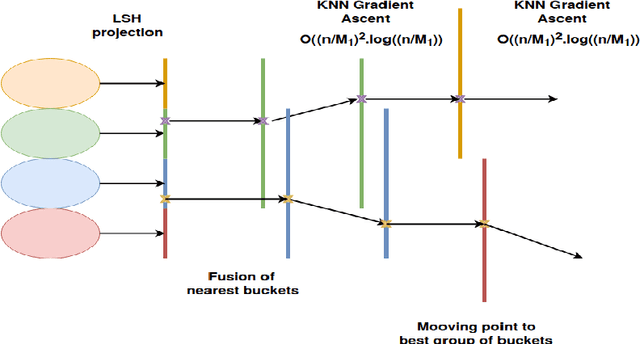
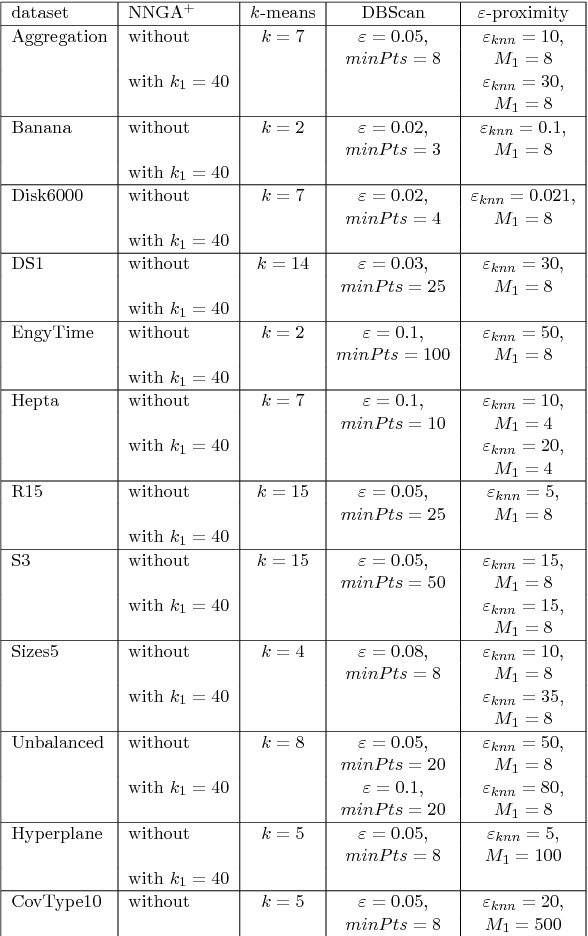
In this paper we target the class of modal clustering methods where clusters are defined in terms of the local modes of the probability density function which generates the data. The most well-known modal clustering method is the k-means clustering. Mean Shift clustering is a generalization of the k-means clustering which computes arbitrarily shaped clusters as defined as the basins of attraction to the local modes created by the density gradient ascent paths. Despite its potential, the Mean Shift approach is a computationally expensive method for unsupervised learning. Thus, we introduce two contributions aiming to provide clustering algorithms with a linear time complexity, as opposed to the quadratic time complexity for the exact Mean Shift clustering. Firstly we propose a scalable procedure to approximate the density gradient ascent. Second, our proposed scalable cluster labeling technique is presented. Both propositions are based on Locality Sensitive Hashing (LSH) to approximate nearest neighbors. These two techniques may be used for moderate sized datasets. Furthermore, we show that using our proposed approximations of the density gradient ascent as a pre-processing step in other clustering methods can also improve dedicated classification metrics. For the latter, a distributed implementation, written for the Spark/Scala ecosystem is proposed. For all these considered clustering methods, we present experimental results illustrating their labeling accuracy and their potential to solve concrete problems.