Joint Modeling and Registration of Cell Populations in Cohorts of High-Dimensional Flow Cytometric Data

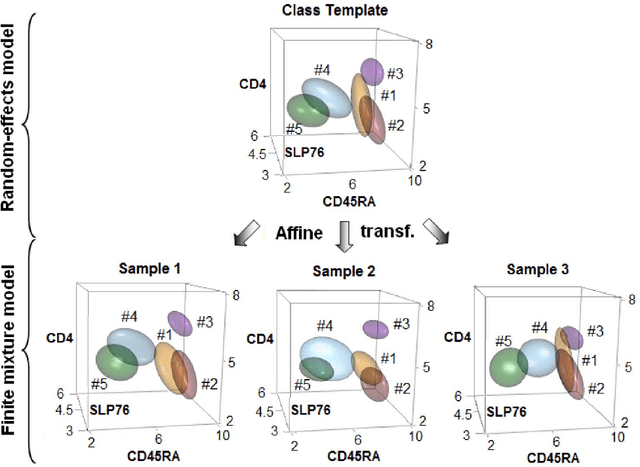
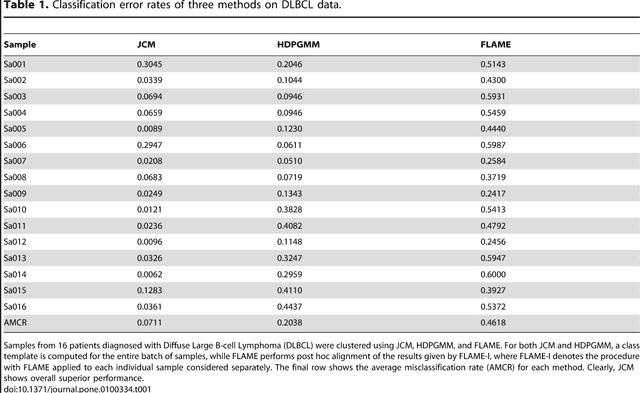
In systems biomedicine, an experimenter encounters different potential sources of variation in data such as individual samples, multiple experimental conditions, and multi-variable network-level responses. In multiparametric cytometry, which is often used for analyzing patient samples, such issues are critical. While computational methods can identify cell populations in individual samples, without the ability to automatically match them across samples, it is difficult to compare and characterize the populations in typical experiments, such as those responding to various stimulations or distinctive of particular patients or time-points, especially when there are many samples. Joint Clustering and Matching (JCM) is a multi-level framework for simultaneous modeling and registration of populations across a cohort. JCM models every population with a robust multivariate probability distribution. Simultaneously, JCM fits a random-effects model to construct an overall batch template -- used for registering populations across samples, and classifying new samples. By tackling systems-level variation, JCM supports practical biomedical applications involving large cohorts.

A Very Fast Algorithm for Matrix Factorization

We present a very fast algorithm for general matrix factorization of a data matrix for use in the statistical analysis of high-dimensional data via latent factors. Such data are prevalent across many application areas and generate an ever-increasing demand for methods of dimension reduction in order to undertake the statistical analysis of interest. Our algorithm uses a gradient-based approach which can be used with an arbitrary loss function provided the latter is differentiable. The speed and effectiveness of our algorithm for dimension reduction is demonstrated in the context of supervised classification of some real high-dimensional data sets from the bioinformatics literature.