Bayesian taut splines for estimating the number of modes

The number of modes in a probability density function is representative of the model's complexity and can also be viewed as the number of existing subpopulations. Despite its relevance, little research has been devoted to its estimation. Focusing on the univariate setting, we propose a novel approach targeting prediction accuracy inspired by some overlooked aspects of the problem. We argue for the need for structure in the solutions, the subjective and uncertain nature of modes, and the convenience of a holistic view blending global and local density properties. Our method builds upon a combination of flexible kernel estimators and parsimonious compositional splines. Feature exploration, model selection and mode testing are implemented in the Bayesian inference paradigm, providing soft solutions and allowing to incorporate expert judgement in the process. The usefulness of our proposal is illustrated through a case study in sports analytics, showcasing multiple companion visualisation tools. A thorough simulation study demonstrates that traditional modality-driven approaches paradoxically struggle to provide accurate results. In this context, our method emerges as a top-tier alternative offering innovative solutions for analysts.

Bump hunting through density curvature features

Bump hunting deals with finding in sample spaces meaningful data subsets known as bumps. These have traditionally been conceived as modal or concave regions in the graph of the underlying density function. We define an abstract bump construct based on curvature functionals of the probability density. Then, we explore several alternative characterizations involving derivatives up to second order. In particular, a suitable implementation of Good and Gaskins' original concave bumps is proposed in the multivariate case. Moreover, we bring to exploratory data analysis concepts like the mean curvature and the Laplacian that have produced good results in applied domains. Our methodology addresses the approximation of the curvature functional with a plug-in kernel density estimator. We provide theoretical results that assure the asymptotic consistency of bump boundaries in the Hausdorff distance with affordable convergence rates. We also present asymptotically valid and consistent confidence regions bounding curvature bumps. The theory is illustrated through several use cases in sports analytics with datasets from the NBA, MLB and NFL. We conclude that the different curvature instances effectively combine to generate insightful visualizations.

Minimum adjusted Rand index for two clusterings of a given size

In an unpublished presentation, Steinley reported that the minimum adjusted Rand index for the comparison of two clusterings of size $r$ is $-1/r$. However, in a subsequent paper Chac\'on noted that this apparent bound can be lowered. Here, it is shown that the lower bound proposed by Chac\'on is indeed the minimum possible one. The result is even more general, since it is valid for two clusterings of possibly different sizes.

Explicit agreement extremes for a $2\times2$ table with given marginals

The problem of maximizing (or minimizing) the agreement between clusterings, subject to given marginals, can be formally posed under a common framework for several agreement measures. Until now, it was possible to find its solution only through numerical algorithms. Here, an explicit solution is shown for the case where the two clusterings have two clusters each.

A close-up comparison of the misclassification error distance and the adjusted Rand index for external clustering evaluation

The misclassification error distance and the adjusted Rand index are two of the most commonly used criteria to evaluate the performance of clustering algorithms. This paper provides an in-depth comparison of the two criteria, aimed to better understand exactly what they measure, their properties and their differences. Starting from their population origins, the investigation includes many data analysis examples and the study of particular cases in great detail. An exhaustive simulation study allows inspecting the criteria distributions and reveals some previous misconceptions.

Modal clustering asymptotics with applications to bandwidth selection

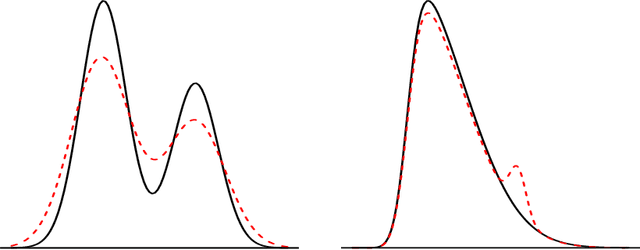
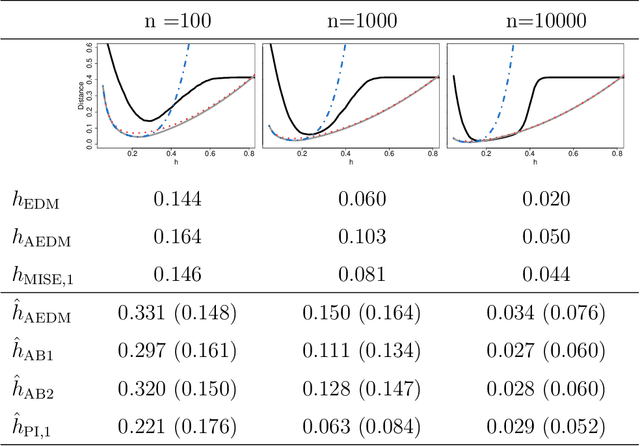
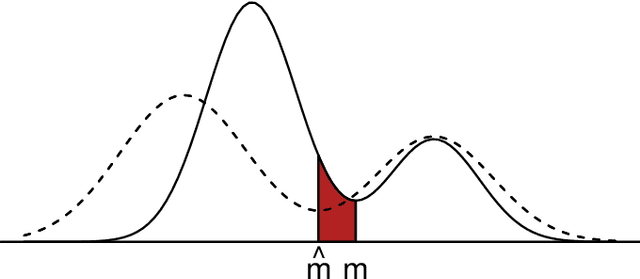
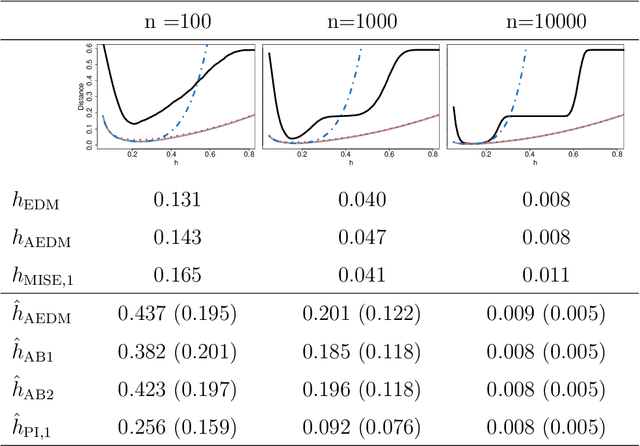
Density-based clustering relies on the idea of linking groups to some specific features of the probability distribution underlying the data. The reference to a true, yet unknown, population structure allows to frame the clustering problem in a standard inferential setting, where the concept of ideal population clustering is defined as the partition induced by the true density function. The nonparametric formulation of this approach, known as modal clustering, draws a correspondence between the groups and the domains of attraction of the density modes. Operationally, a nonparametric density estimate is required and a proper selection of the amount of smoothing, governing the shape of the density and hence possibly the modal structure, is crucial to identify the final partition. In this work, we address the issue of density estimation for modal clustering from an asymptotic perspective. A natural and easy to interpret metric to measure the distance between density-based partitions is discussed, its asymptotic approximation explored, and employed to study the problem of bandwidth selection for nonparametric modal clustering.

The modal age of Statistics

Recently, a number of statistical problems have found an unexpected solution by inspecting them through a "modal point of view". These include classical tasks such as clustering or regression. This has led to a renewed interest in estimation and inference for the mode. This paper offers an extensive survey of the traditional approaches to mode estimation and explores the consequences of applying this modern modal methodology to other, seemingly unrelated, fields.

Mixture model modal clustering

The two most extended density-based approaches to clustering are surely mixture model clustering and modal clustering. In the mixture model approach, the density is represented as a mixture and clusters are associated to the different mixture components. In modal clustering, clusters are understood as regions of high density separated from each other by zones of lower density, so that they are closely related to certain regions around the density modes. If the true density is indeed in the assumed class of mixture densities, then mixture model clustering allows to scrutinize more subtle situations than modal clustering. However, when mixture modeling is used in a nonparametric way, taking advantage of the denseness of the sieve of mixture densities to approximate any density, then the correspondence between clusters and mixture components may become questionable. In this paper we introduce two methods to adopt a modal clustering point of view after a mixture model fit. Numerous examples are provided to illustrate that mixture modeling can also be used for clustering in a nonparametric sense, as long as clusters are understood as the domains of attraction of the density modes.

A Population Background for Nonparametric Density-Based Clustering

Despite its popularity, it is widely recognized that the investigation of some theoretical aspects of clustering has been relatively sparse. One of the main reasons for this lack of theoretical results is surely the fact that, whereas for other statistical problems the theoretical population goal is clearly defined (as in regression or classification), for some of the clustering methodologies it is difficult to specify the population goal to which the data-based clustering algorithms should try to get close. This paper aims to provide some insight into the theoretical foundations of clustering by focusing on two main objectives: to provide an explicit formulation for the ideal population goal of the modal clustering methodology, which understands clusters as regions of high density; and to present two new loss functions, applicable in fact to any clustering methodology, to evaluate the performance of a data-based clustering algorithm with respect to the ideal population goal. In particular, it is shown that only mild conditions on a sequence of density estimators are needed to ensure that the sequence of modal clusterings that they induce is consistent.

A comparison of bandwidth selectors for mean shift clustering

We explore the performance of several automatic bandwidth selectors, originally designed for density gradient estimation, as data-based procedures for nonparametric, modal clustering. The key tool to obtain a clustering from density gradient estimators is the mean shift algorithm, which allows to obtain a partition not only of the data sample, but also of the whole space. The results of our simulation study suggest that most of the methods considered here, like cross validation and plug in bandwidth selectors, are useful for cluster analysis via the mean shift algorithm.