Giovanna Menardi
Advanced Multi-Variate Analysis Methods for New Physics Searches at the Large Hadron Collider
May 16, 2021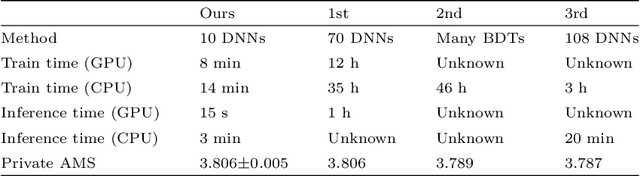
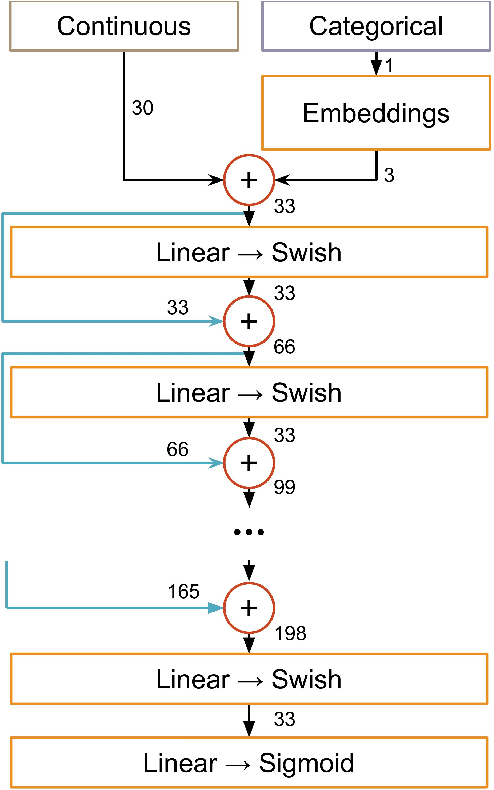
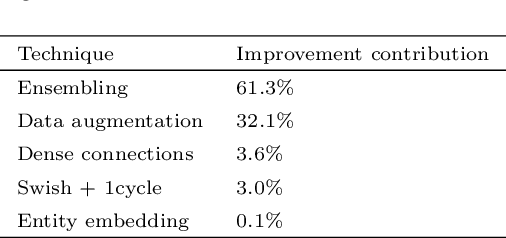
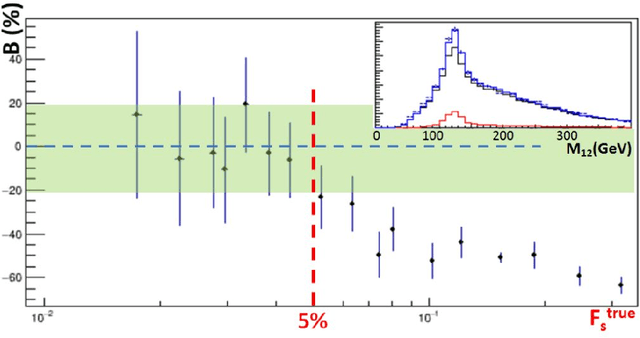
Abstract:Between the years 2015 and 2019, members of the Horizon 2020-funded Innovative Training Network named "AMVA4NewPhysics" studied the customization and application of advanced multivariate analysis methods and statistical learning tools to high-energy physics problems, as well as developed entirely new ones. Many of those methods were successfully used to improve the sensitivity of data analyses performed by the ATLAS and CMS experiments at the CERN Large Hadron Collider; several others, still in the testing phase, promise to further improve the precision of measurements of fundamental physics parameters and the reach of searches for new phenomena. In this paper, the most relevant new tools, among those studied and developed, are presented along with the evaluation of their performances.
Nonparametric clustering for image segmentation
Jan 20, 2021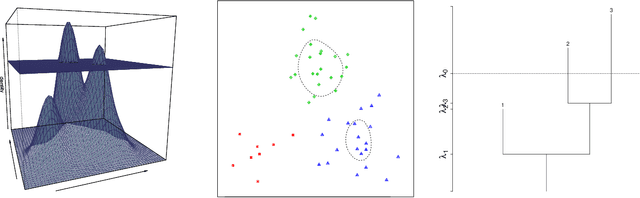
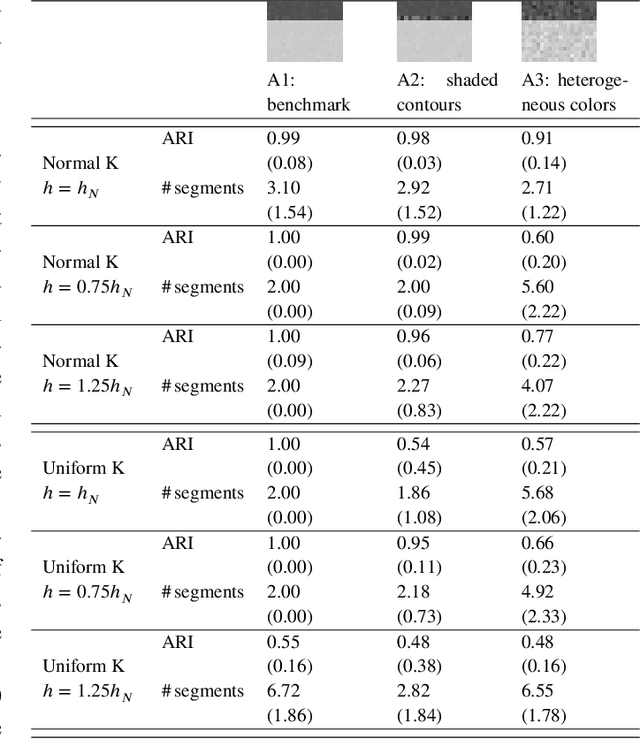

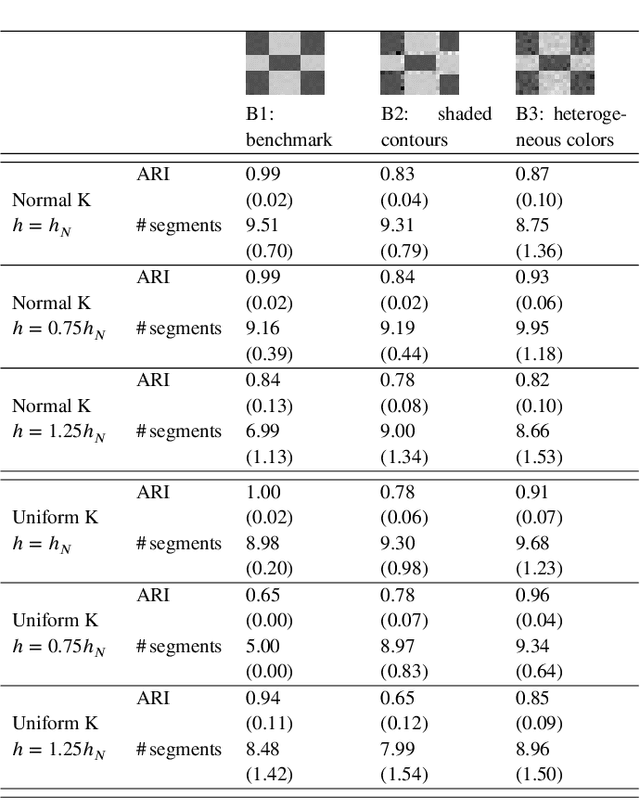
Abstract:Image segmentation aims at identifying regions of interest within an image, by grouping pixels according to their properties. This task resembles the statistical one of clustering, yet many standard clustering methods fail to meet the basic requirements of image segmentation: segment shapes are often biased toward predetermined shapes and their number is rarely determined automatically. Nonparametric clustering is, in principle, free from these limitations and turns out to be particularly suitable for the task of image segmentation. This is also witnessed by several operational analogies, as, for instance, the resort to topological data analysis and spatial tessellation in both the frameworks. We discuss the application of nonparametric clustering to image segmentation and provide an algorithm specific for this task. Pixel similarity is evaluated in terms of density of the color representation and the adjacency structure of the pixels is exploited to introduce a simple, yet effective method to identify image segments as disconnected high-density regions. The proposed method works both to segment an image and to detect its boundaries and can be seen as a generalization to color images of the class of thresholding methods.
Modal clustering asymptotics with applications to bandwidth selection
Jan 22, 2019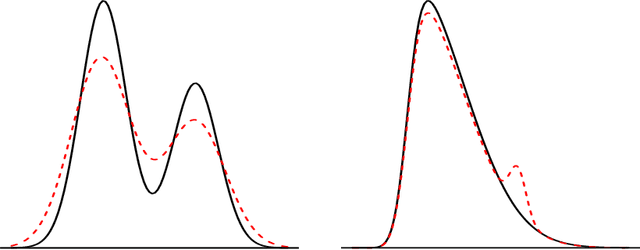
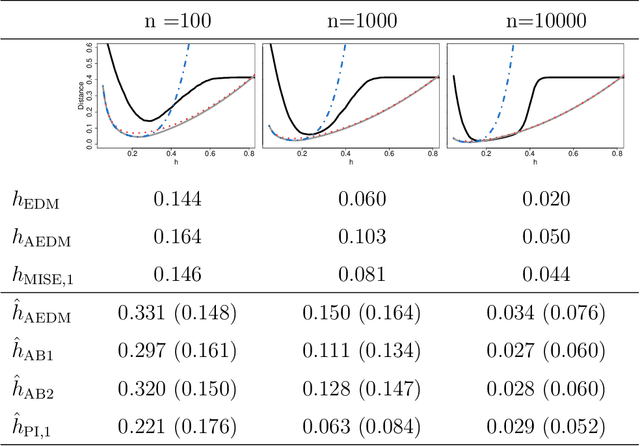
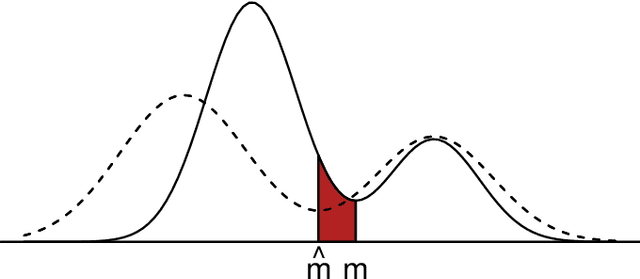
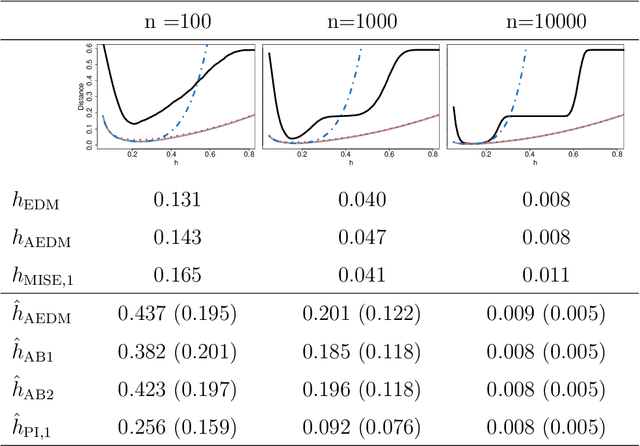
Abstract:Density-based clustering relies on the idea of linking groups to some specific features of the probability distribution underlying the data. The reference to a true, yet unknown, population structure allows to frame the clustering problem in a standard inferential setting, where the concept of ideal population clustering is defined as the partition induced by the true density function. The nonparametric formulation of this approach, known as modal clustering, draws a correspondence between the groups and the domains of attraction of the density modes. Operationally, a nonparametric density estimate is required and a proper selection of the amount of smoothing, governing the shape of the density and hence possibly the modal structure, is crucial to identify the final partition. In this work, we address the issue of density estimation for modal clustering from an asymptotic perspective. A natural and easy to interpret metric to measure the distance between density-based partitions is discussed, its asymptotic approximation explored, and employed to study the problem of bandwidth selection for nonparametric modal clustering.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge