Continuous-Time State Estimation Methods in Robotics: A Survey

Accurate, efficient, and robust state estimation is more important than ever in robotics as the variety of platforms and complexity of tasks continue to grow. Historically, discrete-time filters and smoothers have been the dominant approach, in which the estimated variables are states at discrete sample times. The paradigm of continuous-time state estimation proposes an alternative strategy by estimating variables that express the state as a continuous function of time, which can be evaluated at any query time. Not only can this benefit downstream tasks such as planning and control, but it also significantly increases estimator performance and flexibility, as well as reduces sensor preprocessing and interfacing complexity. Despite this, continuous-time methods remain underutilized, potentially because they are less well-known within robotics. To remedy this, this work presents a unifying formulation of these methods and the most exhaustive literature review to date, systematically categorizing prior work by methodology, application, state variables, historical context, and theoretical contribution to the field. By surveying splines and Gaussian processes together and contextualizing works from other research domains, this work identifies and analyzes open problems in continuous-time state estimation and suggests new research directions.

A Data-driven Contact Estimation Method for Wheeled-Biped Robots

Contact estimation is a key ability for limbed robots, where making and breaking contacts has a direct impact on state estimation and balance control. Existing approaches typically rely on gate-cycle priors or designated contact sensors. We design a contact estimator that is suitable for the emerging wheeled-biped robot types that do not have these features. To this end, we propose a Bayes filter in which update steps are learned from real-robot torque measurements while prediction steps rely on inertial measurements. We evaluate this approach in extensive real-robot and simulation experiments. Our method achieves better performance while being considerably more sample efficient than a comparable deep-learning baseline.

Exploiting Chordal Sparsity for Fast Global Optimality with Application to Localization

In recent years, many estimation problems in robotics have been shown to be solvable to global optimality using their semidefinite relaxations. However, the runtime complexity of off-the-shelve semidefinite programming solvers is up to cubic in problem size, which inhibits real-time solutions of problems involving large state dimensions. We show that for a large class of problems, namely those with chordal sparsity, we can reduce the complexity of these solvers to linear in problem size. In particular, we show how to replace the large positive-semidefinite variable by a number of smaller interconnected ones using the well-known chordal decomposition. This formulation also allows for the straightforward application of the alternating direction method of multipliers (ADMM), which can exploit parallelism for increased scalability. We show in simulation that the algorithms provide a significant speed up for two example problems: matrix-weighted and range-only localization.

SDPRLayers: Certifiable Backpropagation Through Polynomial Optimization Problems in Robotics

Differentiable optimization is a powerful new paradigm capable of reconciling model-based and learning-based approaches in robotics. However, the majority of robotics optimization problems are non-convex and current differentiable optimization techniques are therefore prone to convergence to local minima. When this occurs, the gradients provided by these existing solvers can be wildly inaccurate and will ultimately corrupt the training process. On the other hand, any non-convex robotics problems can be framed as polynomial optimization problems and, in turn, admit convex relaxations that can be used to recover a global solution via so-called certifiably correct methods. We present SDPRLayers, an approach that leverages these methods as well as state-of-the-art convex implicit differentiation techniques to provide certifiably correct gradients throughout the training process. We introduce this approach and showcase theoretical results that provide conditions under which correctness of the gradients is guaranteed. We demonstrate our approach on two simple-but-demonstrative simulated examples, which expose the potential pitfalls of existing, state-of-the-art, differentiable optimization methods. We apply our method in a real-world application: we train a deep neural network to detect image keypoints for robot localization in challenging lighting conditions. An open-source, PyTorch implementation of SDPRLayers will be made available upon paper acceptance.

Safe and Efficient Estimation for Robotics through the Optimal Use of Resources

In order to operate in and interact with the physical world, robots need to have estimates of the current and future state of the environment. We thus equip robots with sensors and build models and algorithms that, given some measurements, produce estimates of the current or future states. Environments can be unpredictable and sensors are not perfect. Therefore, it is important to both use all information available, and to do so optimally: making sure that we get the best possible answer from the amount of information we have. However, in prevalent research, uncommon sensors, such as sound or radio-frequency signals, are commonly ignored for state estimation; and the most popular solvers employed to produce state estimates are only of local nature, meaning they may produce suboptimal estimates for the typically non-convex estimation problems. My research aims to use resources more optimally, by building on 1) multi-modality: using ubiquitous RF transceivers and microphones to support state estimation, 2) building certifiably optimal solvers and 3) learning and improving adequate models from data.

Optimal Initialization Strategies for Range-Only Trajectory Estimation

Range-only (RO) pose estimation involves determining a robot's pose over time by measuring the distance between multiple devices on the robot, known as tags, and devices installed in the environment, known as anchors. The nonconvex nature of the range measurement model results in a cost function with possible local minima. In the absence of a good initialization, commonly used iterative solvers can get stuck in these local minima resulting in poor trajectory estimation accuracy. In this work, we propose convex relaxations to the original nonconvex problem based on semidefinite programs (SDPs). Specifically, we formulate computationally tractable SDP relaxations to obtain accurate initial pose and trajectory estimates for RO trajectory estimation under static and dynamic (i.e., constant-velocity motion) conditions. Through simulation and real experiments, we demonstrate that our proposed initialization strategies estimate the initial state accurately compared to iterative local solvers. Additionally, the proposed relaxations recover global minima under moderate range measurement noise levels.

STAR-loc: Dataset for STereo And Range-based localization

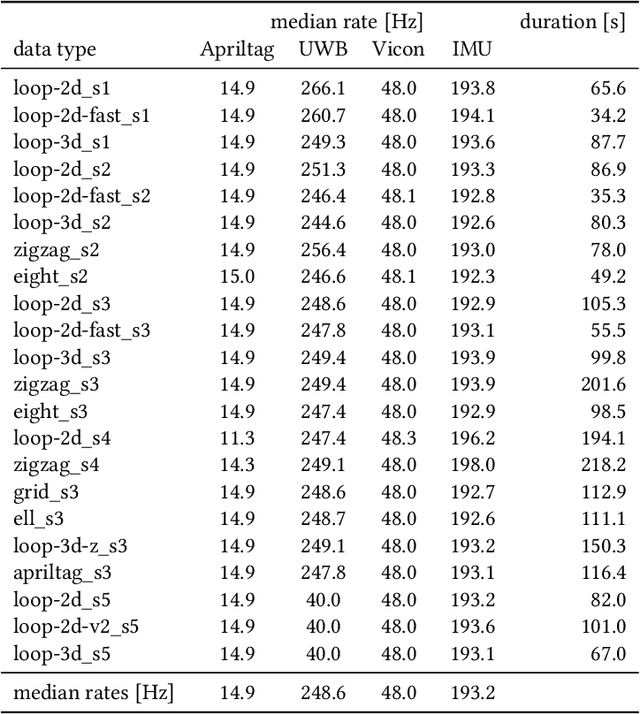
This document contains a detailed description of the STAR-loc dataset. For a quick starting guide please refer to the associated Github repository (https://github.com/utiasASRL/starloc). The dataset consists of stereo camera data (rectified/raw images and inertial measurement unit measurements) and ultra-wideband (UWB) data (range measurements) collected on a sensor rig in a Vicon motion capture arena. The UWB anchors and visual landmarks (Apriltags) are of known position, so the dataset can be used for both localization and Simultaneous Localization and Mapping (SLAM).

Data-Driven Batch Localization and SLAM Using Koopman Linearization

We present a framework for model-free batch localization and SLAM. We use lifting functions to map a control-affine system into a high-dimensional space, where both the process model and the measurement model are rendered bilinear. During training, we solve a least-squares problem using groundtruth data to compute the high-dimensional model matrices associated with the lifted system purely from data. At inference time, we solve for the unknown robot trajectory and landmarks through an optimization problem, where constraints are introduced to keep the solution on the manifold of the lifting functions. The problem is efficiently solved using a sequential quadratic program (SQP), where the complexity of an SQP iteration scales linearly with the number of timesteps. Our algorithms, called Reduced Constrained Koopman Linearization Localization (RCKL-Loc) and Reduced Constrained Koopman Linearization SLAM (RCKL-SLAM), are validated experimentally in simulation and on two datasets: one with an indoor mobile robot equipped with a laser rangefinder that measures range to cylindrical landmarks, and one on a golf cart equipped with RFID range sensors. We compare RCKL-Loc and RCKL-SLAM with classic model-based nonlinear batch estimation. While RCKL-Loc and RCKL-SLAM have similar performance compared to their model-based counterparts, they outperform the model-based approaches when the prior model is imperfect, showing the potential benefit of the proposed data-driven technique.

Certifiably Optimal Rotation and Pose Estimation Based on the Cayley Map

We present novel, tight, convex relaxations for rotation and pose estimation problems that can guarantee global optimality via strong Lagrangian duality. Some such relaxations exist in the literature for specific problem setups that assume the matrix von Mises-Fisher distribution (a.k.a., matrix Langevin distribution or chordal distance) for isotropic rotational uncertainty. However, another common way to represent uncertainty for rotations and poses is to define anisotropic noise in the associated Lie algebra. Starting from a noise model based on the Cayley map, we define our estimation problems, convert them to Quadratically Constrained Quadratic Programs (QCQPs), then relax them to Semidefinite Programs (SDPs), which can be solved using standard interior-point optimization methods. We first show how to carry out basic rotation and pose averaging. We then turn to the more complex problem of trajectory estimation, which involves many pose variables with both individual and inter-pose measurements (or motion priors). Our contribution is to formulate SDP relaxations for all these problems, including the identification of sufficient redundant constraints to make them tight. We hope our results can add to the catalogue of useful estimation problems whose global optimality can be guaranteed.

On Semidefinite Relaxations for Matrix-Weighted State-Estimation Problems in Robotics

In recent years, there has been remarkable progress in the development of so-called certifiable perception methods, which leverage semidefinite, convex relaxations to find global optima of perception problems in robotics. However, many of these relaxations rely on simplifying assumptions that facilitate the problem formulation, such as an isotropic measurement noise distribution. In this paper, we explore the tightness of the semidefinite relaxations of matrix-weighted (anisotropic) state-estimation problems and reveal the limitations lurking therein: matrix-weighted factors can cause convex relaxations to lose tightness. In particular, we show that the semidefinite relaxations of localization problems with matrix weights may be tight only for low noise levels. We empirically explore the factors that contribute to this loss of tightness and demonstrate that redundant constraints can be used to regain tightness, albeit at the expense of real-time performance. As a second technical contribution of this paper, we show that the state-of-the-art relaxation of scalar-weighted SLAM cannot be used when matrix weights are considered. We provide an alternate formulation and show that its SDP relaxation is not tight (even for very low noise levels) unless specific redundant constraints are used. We demonstrate the tightness of our formulations on both simulated and real-world data.