KILO-EKF: Koopman-Inspired Learned Observations Extended Kalman Filter

We present the Koopman-Inspired Learned Observations Extended Kalman Filter (KILO-EKF), which combines a standard EKF prediction step with a correction step based on a Koopman-inspired measurement model learned from data. By lifting measurements into a feature space where they are linear in the state, KILO-EKF enables flexible modeling of complex or poorly calibrated sensors while retaining the structure and efficiency of recursive filtering. The resulting linear-Gaussian measurement model is learned in closed form from groundtruth training data, without iterative optimization or reliance on an explicit parametric sensor model. At inference, KILO-EKF performs a standard EKF update using Jacobians obtained via the learned lifting. We validate the approach on a real-world quadrotor localization task using an IMU, ultra-wideband (UWB) sensors, and a downward-facing laser. We compare against multiple EKF baselines with varying levels of sensor calibration. KILO-EKF achieves better accuracy and consistency compared to data-calibrated baselines, and significantly outperforms EKFs that rely on imperfect geometric models, while maintaining real-time inference and fast training. These results demonstrate the effectiveness of Koopman-inspired measurement learning as a scalable alternative to traditional model-based calibration.

Marginalizing and Conditioning Gaussians onto Linear Approximations of Smooth Manifolds with Applications in Robotics

We present closed-form expressions for marginalizing and conditioning Gaussians onto linear manifolds, and demonstrate how to apply these expressions to smooth nonlinear manifolds through linearization. Although marginalization and conditioning onto axis-aligned manifolds are well-established procedures, doing so onto non-axis-aligned manifolds is not as well understood. We demonstrate the utility of our expressions through three applications: 1) approximation of the projected normal distribution, where the quality of our linearized approximation increases as problem nonlinearity decreases; 2) covariance extraction in Koopman SLAM, where our covariances are shown to be consistent on a real-world dataset; and 3) covariance extraction in constrained GTSAM, where our covariances are shown to be consistent in simulation.

Data-Driven Batch Localization and SLAM Using Koopman Linearization

We present a framework for model-free batch localization and SLAM. We use lifting functions to map a control-affine system into a high-dimensional space, where both the process model and the measurement model are rendered bilinear. During training, we solve a least-squares problem using groundtruth data to compute the high-dimensional model matrices associated with the lifted system purely from data. At inference time, we solve for the unknown robot trajectory and landmarks through an optimization problem, where constraints are introduced to keep the solution on the manifold of the lifting functions. The problem is efficiently solved using a sequential quadratic program (SQP), where the complexity of an SQP iteration scales linearly with the number of timesteps. Our algorithms, called Reduced Constrained Koopman Linearization Localization (RCKL-Loc) and Reduced Constrained Koopman Linearization SLAM (RCKL-SLAM), are validated experimentally in simulation and on two datasets: one with an indoor mobile robot equipped with a laser rangefinder that measures range to cylindrical landmarks, and one on a golf cart equipped with RFID range sensors. We compare RCKL-Loc and RCKL-SLAM with classic model-based nonlinear batch estimation. While RCKL-Loc and RCKL-SLAM have similar performance compared to their model-based counterparts, they outperform the model-based approaches when the prior model is imperfect, showing the potential benefit of the proposed data-driven technique.

Koopman Linearization for Data-Driven Batch State Estimation of Control-Affine Systems

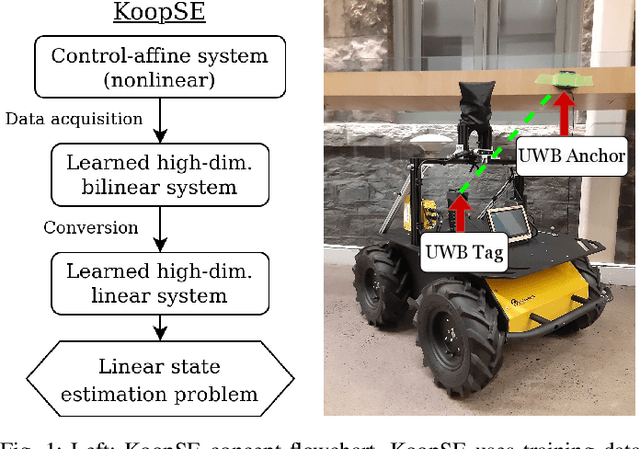
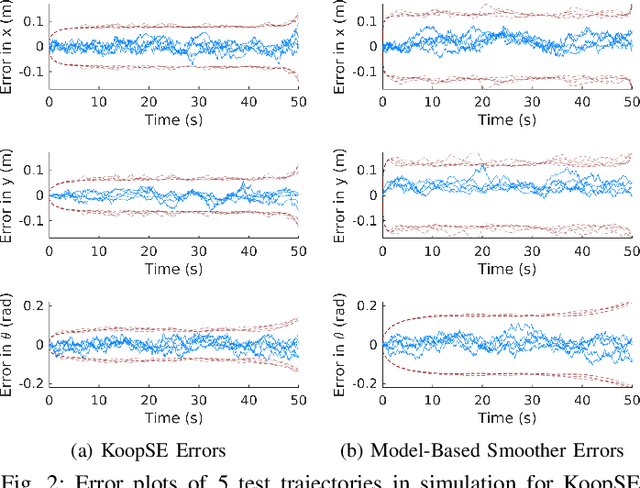
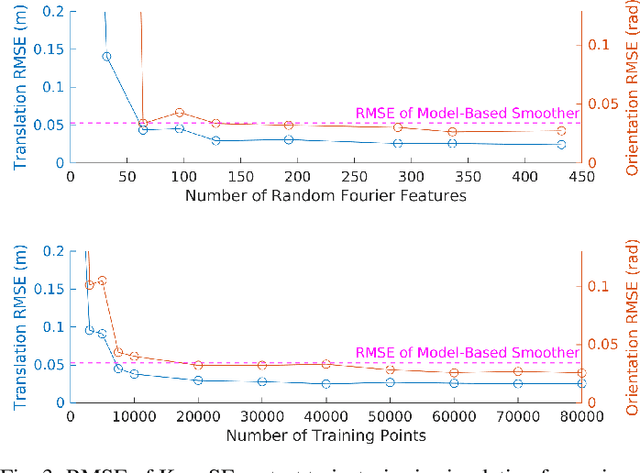
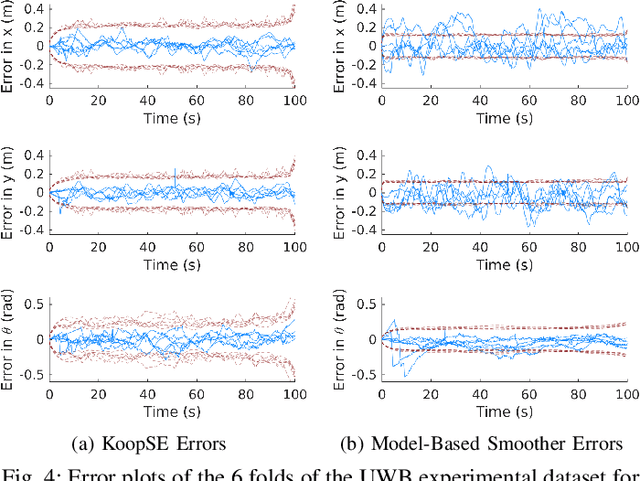
We present the Koopman State Estimator (KoopSE), a framework for model-free batch state estimation of control-affine systems that makes no linearization assumptions, requires no problem-specific feature selections, and has an inference computational cost that is independent of the number of training points. We lift the original nonlinear system into a higher-dimensional Reproducing Kernel Hilbert Space (RKHS), where the system becomes bilinear. The time-invariant model matrices can be learned by solving a least-squares problem on training trajectories. At test time, the system is algebraically manipulated into a linear time-varying system, where standard batch linear state estimation techniques can be used to efficiently compute state means and covariances. Random Fourier Features (RFF) are used to combine the computational efficiency of Koopman-based methods and the generality of kernel-embedding methods. KoopSE is validated experimentally on a localization task involving a mobile robot equipped with ultra-wideband receivers and wheel odometry. KoopSE estimates are more accurate and consistent than the standard model-based extended Rauch-Tung-Striebel (RTS) smoother, despite KoopSE having no prior knowledge of the system's motion or measurement models.