Globally Optimal Data-Association-Free Landmark-Based Localization Using Semidefinite Relaxations

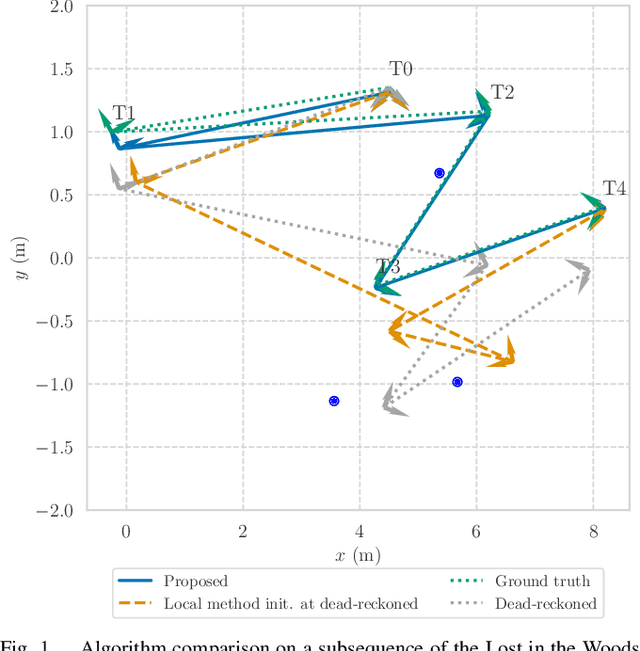
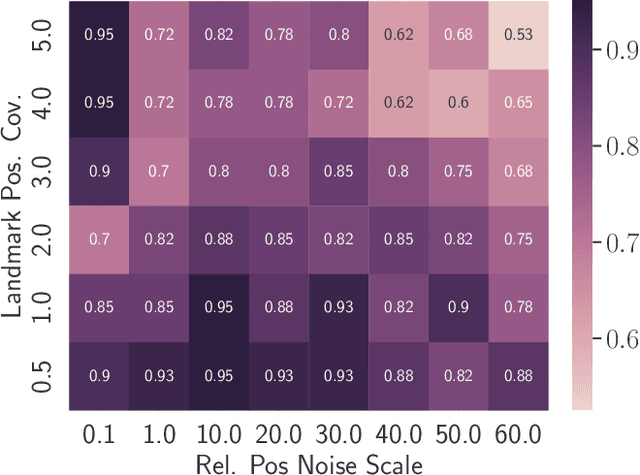
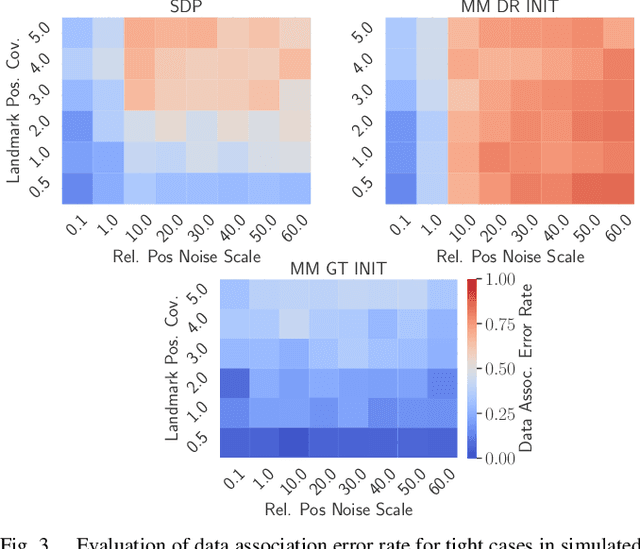
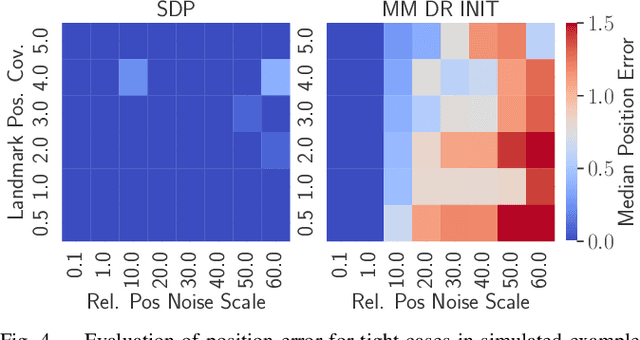
This paper proposes a semidefinite relaxation for landmark-based localization with unknown data associations in planar environments. The proposed method simultaneously solves for the optimal robot states and data associations in a globally optimal fashion. Relative position measurements to known landmarks are used, but the data association is unknown in tha tthe robot does not know which landmark each measurement is generated from. The relaxation is shown to be tight in a majority of cases for moderate noise levels. The proposed algorithm is compared to local Gauss-Newton baselines initialized at the dead-reckoned trajectory, and is shown to significantly improve convergence to the problem's global optimum in simulation and experiment. Accompanying software and supplementary material may be found at https://github.com/vkorotkine/certifiable_uda_loc .

A Hessian for Gaussian Mixture Likelihoods in Nonlinear Least Squares

This paper proposes a novel Hessian approximation for Maximum a Posteriori estimation problems in robotics involving Gaussian mixture likelihoods. The proposed Hessian leads to better convergence properties. Previous approaches manipulate the Gaussian mixture likelihood into a form that allows the problem to be represented as a nonlinear least squares (NLS) problem. However, they result in an inaccurate Hessian approximation due to additional nonlinearities that are not accounted for in NLS solvers. The proposed Hessian approximation is derived by setting the Hessians of the Gaussian mixture component errors to zero, which is the same starting point as for the Gauss-Newton Hessian approximation for NLS, and using the chain rule to account for additional nonlinearities. The proposed Hessian approximation is more accurate, resulting in improved convergence properties that are demonstrated on simulated and real-world experiments. A method to maintain compatibility with existing solvers, such as ceres, is also presented. Accompanying software and supplementary material can be found at https://github.com/decargroup/hessian_sum_mixtures.

navlie: A Python Package for State Estimation on Lie Groups

The ability to rapidly test a variety of algorithms for an arbitrary state estimation task is valuable in the prototyping phase of navigation systems. Lie group theory is now mainstream in the robotics community, and hence estimation prototyping tools should allow state definitions that belong to manifolds. A new package, called navlie, provides a framework that allows a user to model a large class of problems by implementing a set of classes complying with a generic interface. Once accomplished, navlie provides a variety of on-manifold estimation algorithms that can run directly on these classes. The package also provides a built-in library of common models, as well as many useful utilities. The open-source project can be found at https://github.com/decargroup/navlie.

Koopman Linearization for Data-Driven Batch State Estimation of Control-Affine Systems

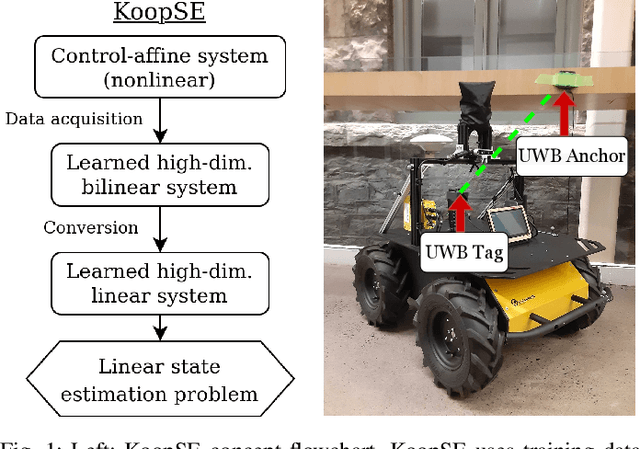
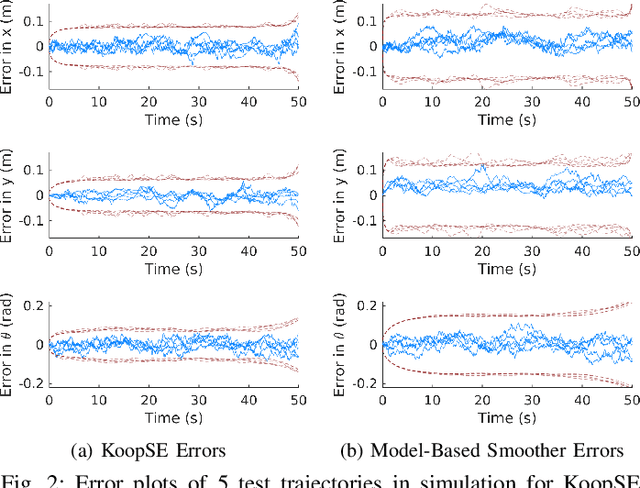
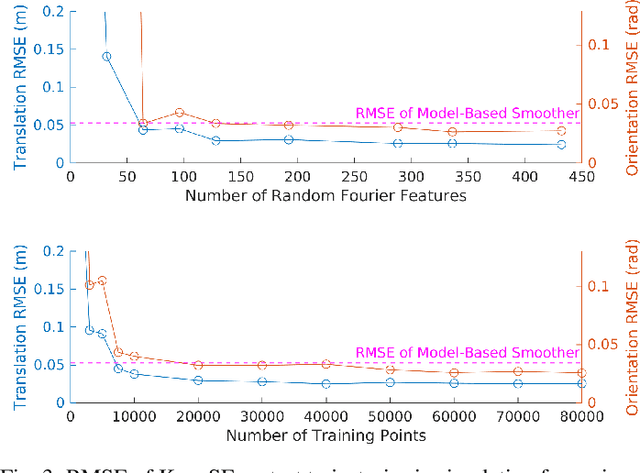
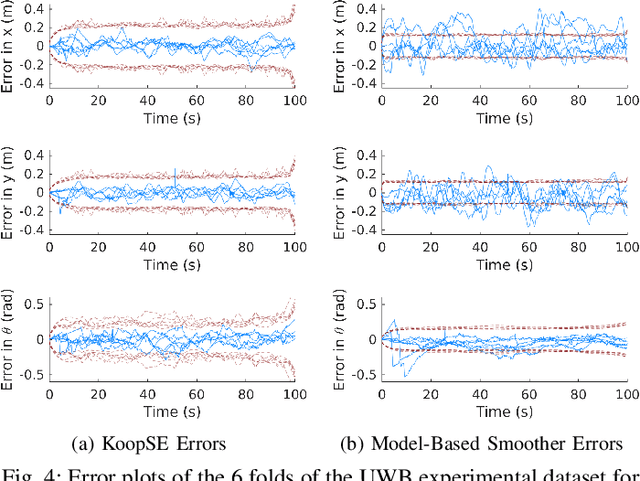
We present the Koopman State Estimator (KoopSE), a framework for model-free batch state estimation of control-affine systems that makes no linearization assumptions, requires no problem-specific feature selections, and has an inference computational cost that is independent of the number of training points. We lift the original nonlinear system into a higher-dimensional Reproducing Kernel Hilbert Space (RKHS), where the system becomes bilinear. The time-invariant model matrices can be learned by solving a least-squares problem on training trajectories. At test time, the system is algebraically manipulated into a linear time-varying system, where standard batch linear state estimation techniques can be used to efficiently compute state means and covariances. Random Fourier Features (RFF) are used to combine the computational efficiency of Koopman-based methods and the generality of kernel-embedding methods. KoopSE is validated experimentally on a localization task involving a mobile robot equipped with ultra-wideband receivers and wheel odometry. KoopSE estimates are more accurate and consistent than the standard model-based extended Rauch-Tung-Striebel (RTS) smoother, despite KoopSE having no prior knowledge of the system's motion or measurement models.