Globally Optimal Data-Association-Free Landmark-Based Localization Using Semidefinite Relaxations

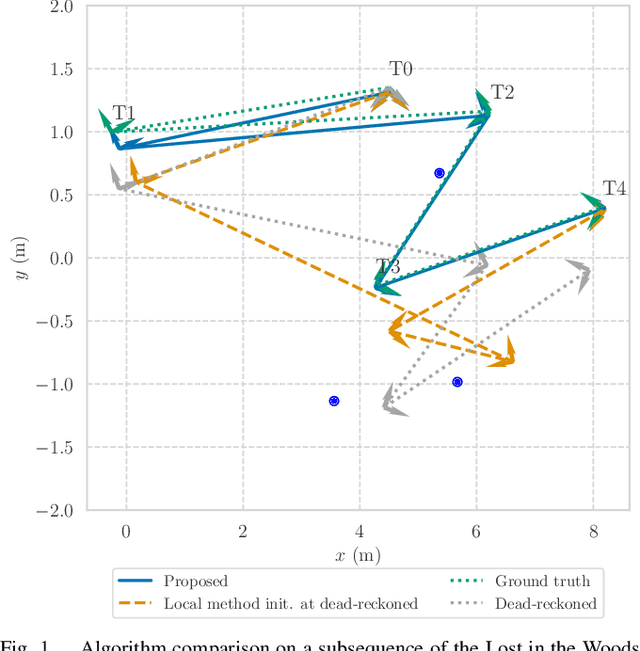
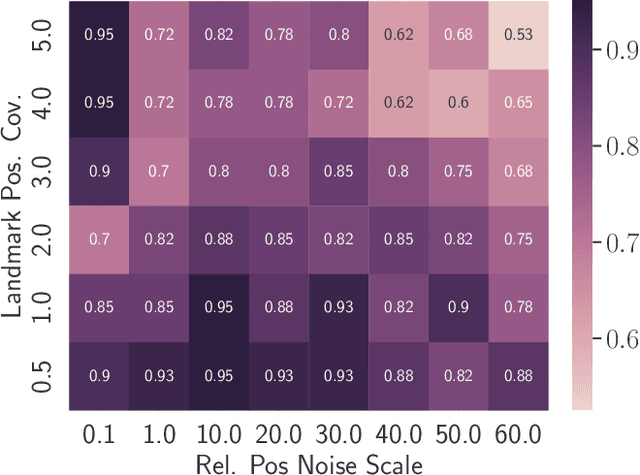
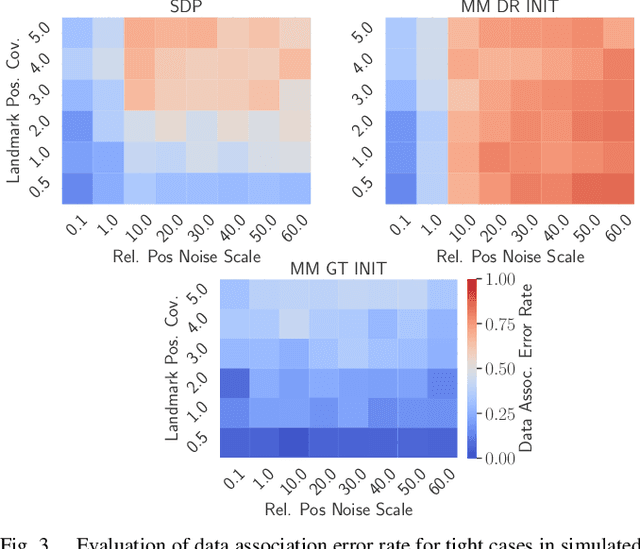
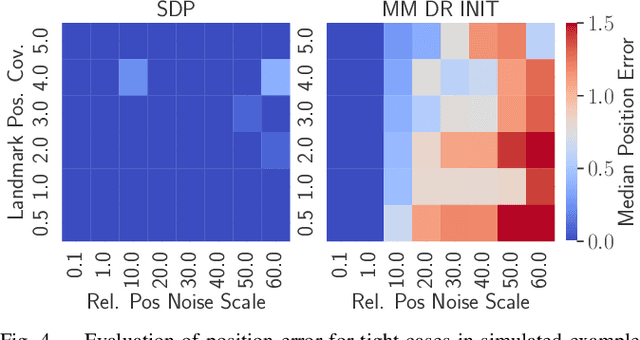
This paper proposes a semidefinite relaxation for landmark-based localization with unknown data associations in planar environments. The proposed method simultaneously solves for the optimal robot states and data associations in a globally optimal fashion. Relative position measurements to known landmarks are used, but the data association is unknown in tha tthe robot does not know which landmark each measurement is generated from. The relaxation is shown to be tight in a majority of cases for moderate noise levels. The proposed algorithm is compared to local Gauss-Newton baselines initialized at the dead-reckoned trajectory, and is shown to significantly improve convergence to the problem's global optimum in simulation and experiment. Accompanying software and supplementary material may be found at https://github.com/vkorotkine/certifiable_uda_loc .

A Hessian for Gaussian Mixture Likelihoods in Nonlinear Least Squares

This paper proposes a novel Hessian approximation for Maximum a Posteriori estimation problems in robotics involving Gaussian mixture likelihoods. The proposed Hessian leads to better convergence properties. Previous approaches manipulate the Gaussian mixture likelihood into a form that allows the problem to be represented as a nonlinear least squares (NLS) problem. However, they result in an inaccurate Hessian approximation due to additional nonlinearities that are not accounted for in NLS solvers. The proposed Hessian approximation is derived by setting the Hessians of the Gaussian mixture component errors to zero, which is the same starting point as for the Gauss-Newton Hessian approximation for NLS, and using the chain rule to account for additional nonlinearities. The proposed Hessian approximation is more accurate, resulting in improved convergence properties that are demonstrated on simulated and real-world experiments. A method to maintain compatibility with existing solvers, such as ceres, is also presented. Accompanying software and supplementary material can be found at https://github.com/decargroup/hessian_sum_mixtures.

Navigation and Control of Unconventional VTOL UAVs in Forward-Flight with Explicit Wind Velocity Estimation

This paper presents a solution for the state estimation and control problems for a class of unconventional vertical takeoff and landing (VTOL) UAVs operating in forward-flight conditions. A tightly-coupled state estimation approach is used to estimate the aircraft navigation states, sensor biases, and the wind velocity. State estimation is done within a matrix Lie group framework using the Invariant Extended Kalman Filter (IEKF), which offers several advantages compared to standard multiplicative EKFs traditionally used in aerospace and robotics problems. An SO(3)- based attitude controller is employed, leading to a single attitude control law without a separate sideslip control loop. A control allocator is used to determine how to use multiple, possibly redundant, actuators to produce the desired control moments. The wind velocity estimates are used in the attitude controller and the control allocator to improve performance. A numerical example is considered using a sample VTOL tailsitter-type UAV with four control surfaces. Monte-Carlo simulations demonstrate robustness of the proposed control and estimation scheme to various initial conditions, noise levels, and flight trajectories.

The Invariant Rauch-Tung-Striebel Smoother

This paper presents an invariant Rauch-Tung- Striebel (IRTS) smoother applicable to systems with states that are an element of a matrix Lie group. In particular, the extended Rauch-Tung-Striebel (RTS) smoother is adapted to work within a matrix Lie group framework. The main advantage of the invariant RTS (IRTS) smoother is that the linearization of the process and measurement models is independent of the state estimate resulting in state-estimate-independent Jacobians when certain technical requirements are met. A sample problem is considered that involves estimation of the three dimensional pose of a rigid body on SE(3), along with sensor biases. The multiplicative RTS (MRTS) smoother is also reviewed and is used as a direct comparison to the proposed IRTS smoother using experimental data. Both smoothing methods are also compared to invariant and multiplicative versions of the Gauss-Newton approach to solving the batch state estimation problem.

navlie: A Python Package for State Estimation on Lie Groups

The ability to rapidly test a variety of algorithms for an arbitrary state estimation task is valuable in the prototyping phase of navigation systems. Lie group theory is now mainstream in the robotics community, and hence estimation prototyping tools should allow state definitions that belong to manifolds. A new package, called navlie, provides a framework that allows a user to model a large class of problems by implementing a set of classes complying with a generic interface. Once accomplished, navlie provides a variety of on-manifold estimation algorithms that can run directly on these classes. The package also provides a built-in library of common models, as well as many useful utilities. The open-source project can be found at https://github.com/decargroup/navlie.

Know What You Don't Know: Consistency in Sliding Window Filtering with Unobservable States Applied to Visual-Inertial SLAM

Estimation algorithms, such as the sliding window filter, produce an estimate and uncertainty of desired states. This task becomes challenging when the problem involves unobservable states. In these situations, it is critical for the algorithm to ``know what it doesn't know'', meaning that it must maintain the unobservable states as unobservable during algorithm deployment. This letter presents general requirements for maintaining consistency in sliding window filters involving unobservable states. The value of these requirements when designing a navigation solution is experimentally shown within the context of visual-inertial SLAM making use of IMU preintegration.