Marginalizing and Conditioning Gaussians onto Linear Approximations of Smooth Manifolds with Applications in Robotics

We present closed-form expressions for marginalizing and conditioning Gaussians onto linear manifolds, and demonstrate how to apply these expressions to smooth nonlinear manifolds through linearization. Although marginalization and conditioning onto axis-aligned manifolds are well-established procedures, doing so onto non-axis-aligned manifolds is not as well understood. We demonstrate the utility of our expressions through three applications: 1) approximation of the projected normal distribution, where the quality of our linearized approximation increases as problem nonlinearity decreases; 2) covariance extraction in Koopman SLAM, where our covariances are shown to be consistent on a real-world dataset; and 3) covariance extraction in constrained GTSAM, where our covariances are shown to be consistent in simulation.

Gaussian-Sum Filter for Range-based 3D Relative Pose Estimation in the Presence of Ambiguities

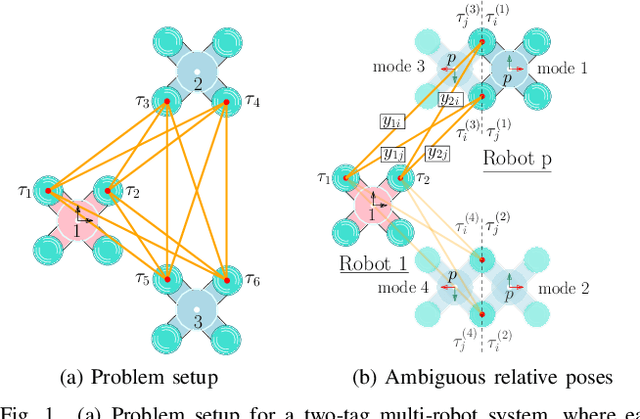
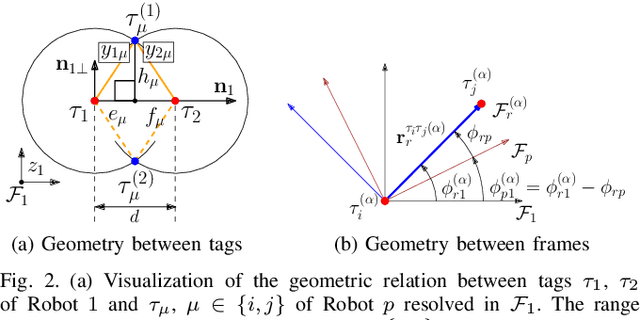
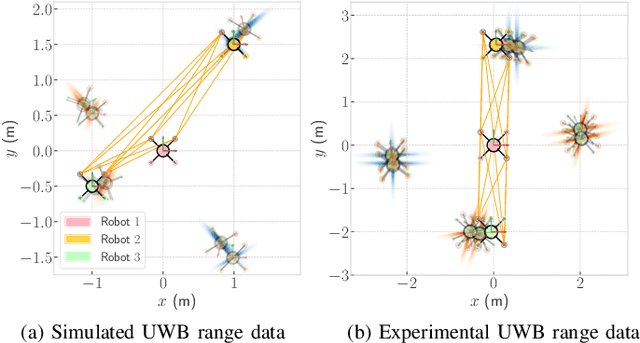
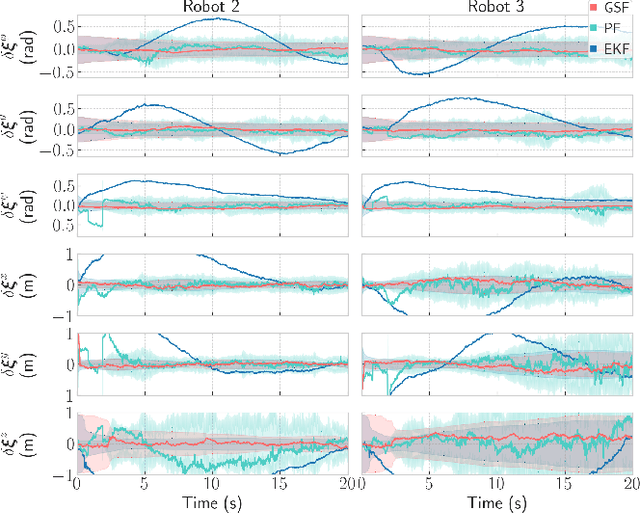
Multi-robot systems must have the ability to accurately estimate relative states between robots in order to perform collaborative tasks, possibly with no external aiding. Three-dimensional relative pose estimation using range measurements oftentimes suffers from a finite number of non-unique solutions, or ambiguities. This paper: 1) identifies and accurately estimates all possible ambiguities in 2D; 2) treats them as components of a Gaussian mixture model; and 3) presents a computationally-efficient estimator, in the form of a Gaussian-sum filter (GSF), to realize range-based relative pose estimation in an infrastructure-free, 3D, setup. This estimator is evaluated in simulation and experiment and is shown to avoid divergence to local minima induced by the ambiguous poses. Furthermore, the proposed GSF outperforms an extended Kalman filter, demonstrates similar performance to the computationally-demanding particle filter, and is shown to be consistent.

STAR-loc: Dataset for STereo And Range-based localization

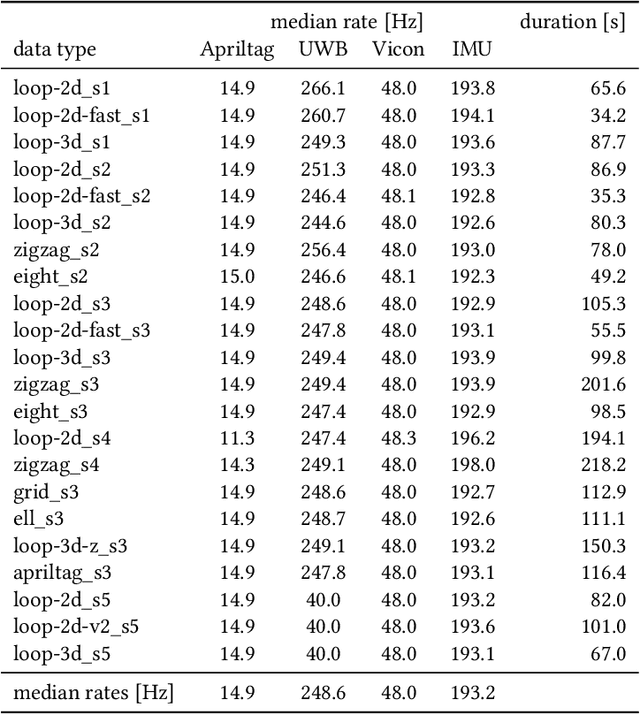
This document contains a detailed description of the STAR-loc dataset. For a quick starting guide please refer to the associated Github repository (https://github.com/utiasASRL/starloc). The dataset consists of stereo camera data (rectified/raw images and inertial measurement unit measurements) and ultra-wideband (UWB) data (range measurements) collected on a sensor rig in a Vicon motion capture arena. The UWB anchors and visual landmarks (Apriltags) are of known position, so the dataset can be used for both localization and Simultaneous Localization and Mapping (SLAM).

Data-Driven Batch Localization and SLAM Using Koopman Linearization

We present a framework for model-free batch localization and SLAM. We use lifting functions to map a control-affine system into a high-dimensional space, where both the process model and the measurement model are rendered bilinear. During training, we solve a least-squares problem using groundtruth data to compute the high-dimensional model matrices associated with the lifted system purely from data. At inference time, we solve for the unknown robot trajectory and landmarks through an optimization problem, where constraints are introduced to keep the solution on the manifold of the lifting functions. The problem is efficiently solved using a sequential quadratic program (SQP), where the complexity of an SQP iteration scales linearly with the number of timesteps. Our algorithms, called Reduced Constrained Koopman Linearization Localization (RCKL-Loc) and Reduced Constrained Koopman Linearization SLAM (RCKL-SLAM), are validated experimentally in simulation and on two datasets: one with an indoor mobile robot equipped with a laser rangefinder that measures range to cylindrical landmarks, and one on a golf cart equipped with RFID range sensors. We compare RCKL-Loc and RCKL-SLAM with classic model-based nonlinear batch estimation. While RCKL-Loc and RCKL-SLAM have similar performance compared to their model-based counterparts, they outperform the model-based approaches when the prior model is imperfect, showing the potential benefit of the proposed data-driven technique.

Koopman Linearization for Data-Driven Batch State Estimation of Control-Affine Systems

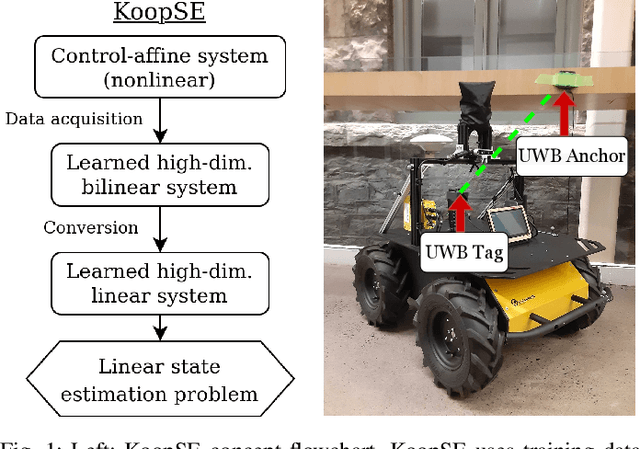
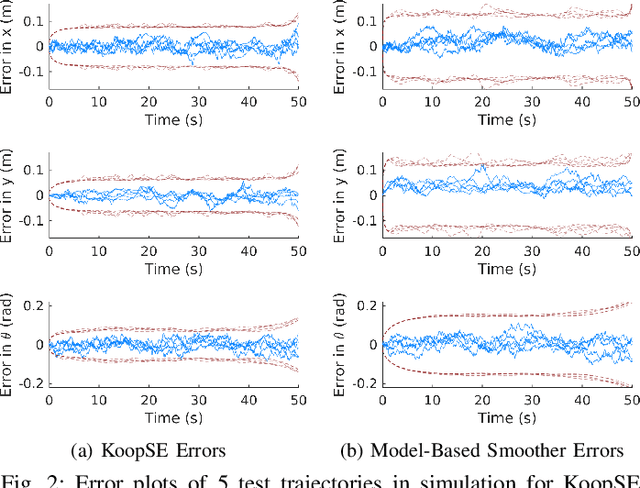
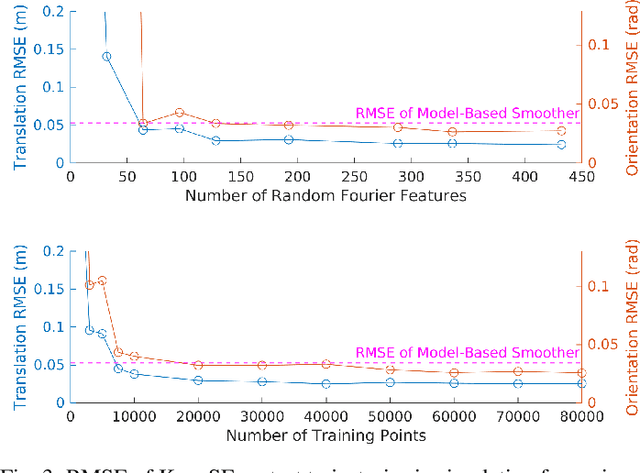
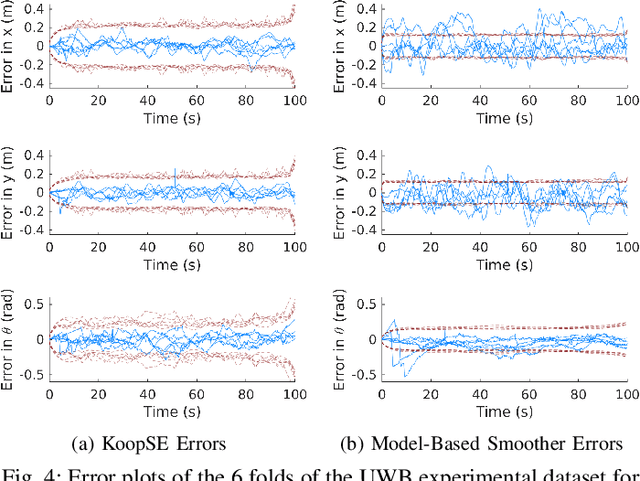
We present the Koopman State Estimator (KoopSE), a framework for model-free batch state estimation of control-affine systems that makes no linearization assumptions, requires no problem-specific feature selections, and has an inference computational cost that is independent of the number of training points. We lift the original nonlinear system into a higher-dimensional Reproducing Kernel Hilbert Space (RKHS), where the system becomes bilinear. The time-invariant model matrices can be learned by solving a least-squares problem on training trajectories. At test time, the system is algebraically manipulated into a linear time-varying system, where standard batch linear state estimation techniques can be used to efficiently compute state means and covariances. Random Fourier Features (RFF) are used to combine the computational efficiency of Koopman-based methods and the generality of kernel-embedding methods. KoopSE is validated experimentally on a localization task involving a mobile robot equipped with ultra-wideband receivers and wheel odometry. KoopSE estimates are more accurate and consistent than the standard model-based extended Rauch-Tung-Striebel (RTS) smoother, despite KoopSE having no prior knowledge of the system's motion or measurement models.

Relative Position Estimation Between Two UWB Devices with IMUs

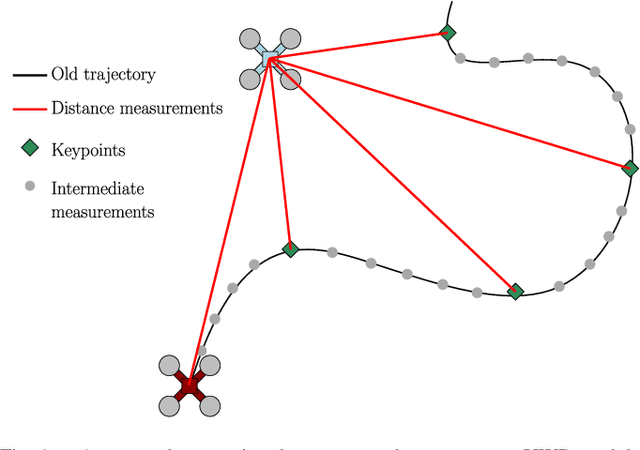
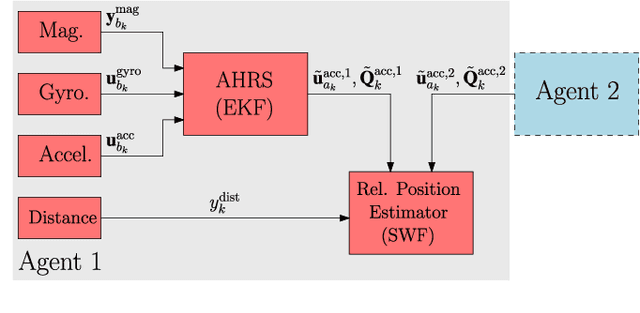
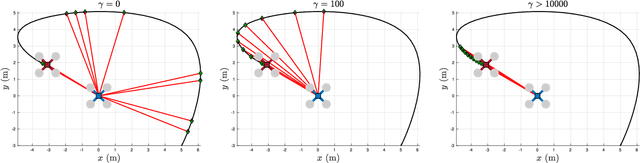
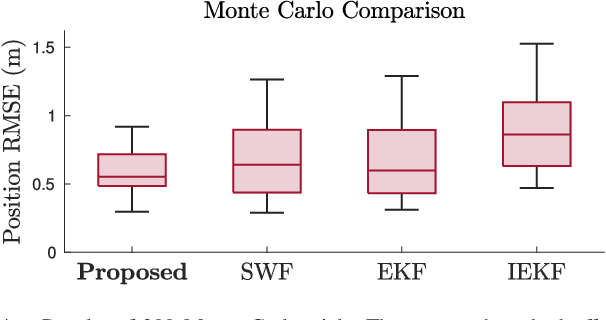
For a team of robots to work collaboratively, it is crucial that each robot have the ability to determine the position of their neighbors, relative to themselves, in order to execute tasks autonomously. This letter presents an algorithm for determining the three-dimensional relative position between two mobile robots, each using nothing more than a single ultra-wideband transceiver, an accelerometer, a rate gyro, and a magnetometer. A sliding window filter estimates the relative position at selected keypoints by combining the distance measurements with acceleration estimates, which each agent computes using an on-board attitude estimator. The algorithm is appropriate for real-time implementation, and has been tested in simulation and experiment, where it comfortably outperforms standard estimators. A positioning accuracy of less than 1 meter is achieved with inexpensive sensors.

Vectorial Parameterizations of Pose

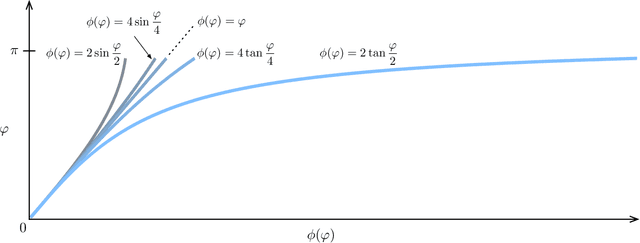
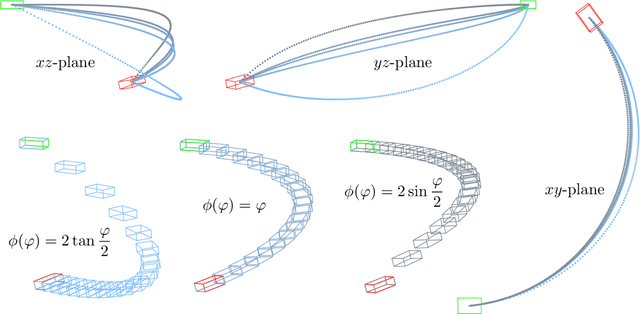
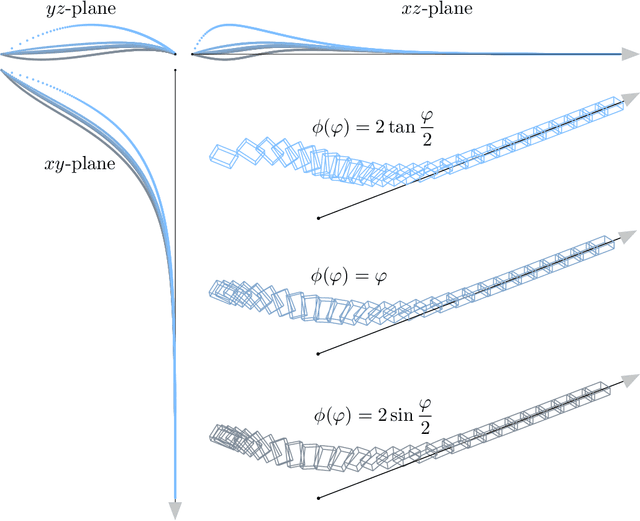
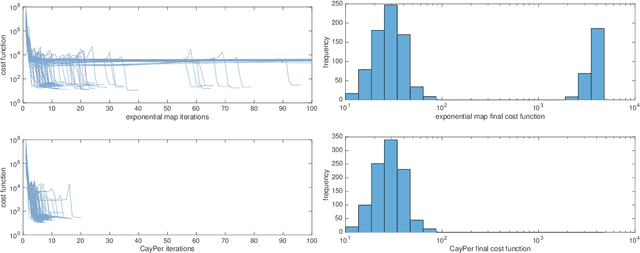
Robotics and computer vision problems commonly require handling rigid-body motions comprising translation and rotation - together referred to as pose. In some situations, a vectorial parameterization of pose can be useful, where elements of a vector space are surjectively mapped to a matrix Lie group. For example, these vectorial representations can be employed for optimization as well as uncertainty representation on groups. The most common mapping is the matrix exponential, which maps elements of a Lie algebra onto the associated Lie group. However, this choice is not unique. It has been previously shown how to characterize all such vectorial parameterizations for SO(3), the group of rotations. We extend this result to SE(3), the group of poses (translation and rotation), showing how to build a family of mappings that includes the matrix exponential as well as the Cayley transformation. While our main contribution is the theory, we also demonstrate three different applications of the proposed pose mappings: (i) pose interpolation, (ii) pose servoing control, and (iii) pose estimation in a pointcloud alignment problem. In the pointcloud alignment problem our results lead to a new algorithm based on the Cayley transformation, which we call CayPer.

Exactly Sparse Gaussian Variational Inference with Application to Derivative-Free Batch Nonlinear State Estimation

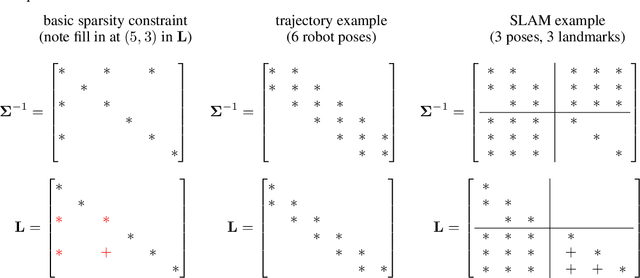
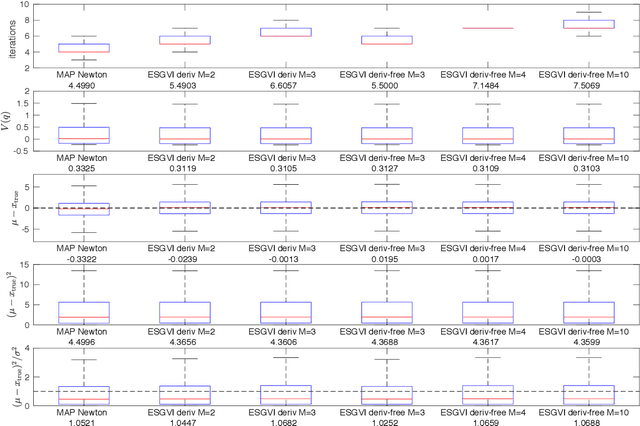
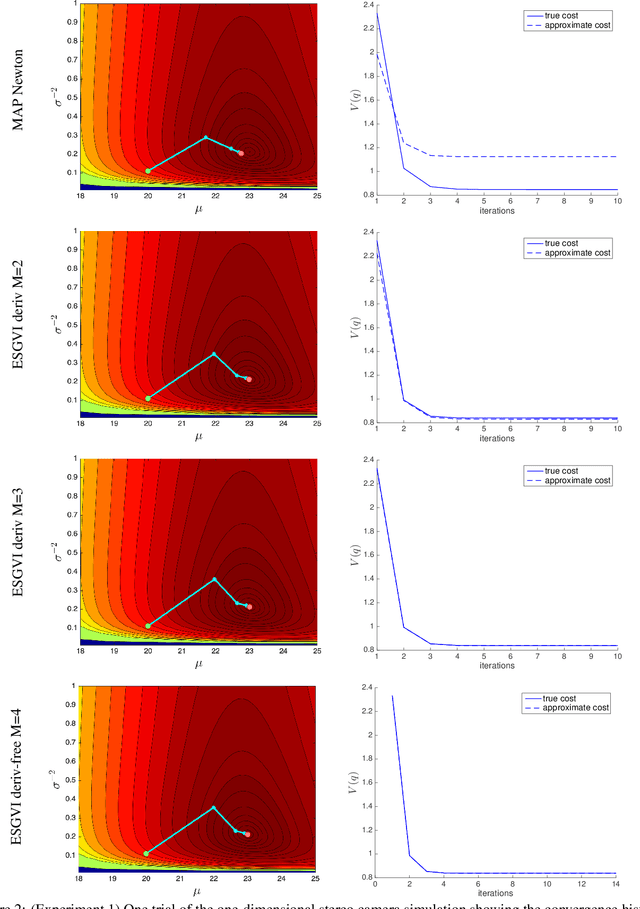
We present a Gaussian Variational Inference (GVI) technique that can be applied to large-scale nonlinear batch state estimation problems. The main contribution is to show how to fit the best Gaussian to the posterior efficiently by exploiting factorization of the joint likelihood of the state and data, as is common in practical problems. The proposed Exactly Sparse Gaussian Variational Inference (ESGVI) technique stores the inverse covariance matrix, which is typically very sparse (e.g., block-tridiagonal for classic state estimation). We show that the only blocks of the (dense) covariance matrix that are required during the calculations correspond to the non-zero blocks of the inverse covariance matrix, and further show how to calculate these blocks efficiently in the general GVI problem. ESGVI operates iteratively, and while we can use analytical derivatives at each iteration, Gaussian cubature can be substituted, thereby producing an efficient derivative-free batch formulation. ESGVI simplifies to precisely the Rauch-Tung-Striebel (RTS) smoother in the batch linear estimation case, but goes beyond the 'extended' RTS smoother in the nonlinear case since it finds the best-fit Gaussian, not the Maximum A Posteriori (MAP) point solution. We demonstrate the technique on controlled simulation problems and a batch nonlinear Simultaneous Localization and Mapping (SLAM) problem with an experimental dataset.