Integral Forms in Matrix Lie Groups

Matrix Lie groups provide a language for describing motion in such fields as robotics, computer vision, and graphics. When using these tools, we are often faced with turning infinite-series expressions into more compact finite series (e.g., the Euler-Rodriques formula), which can sometimes be onerous. In this paper, we identify some useful integral forms in matrix Lie group expressions that offer a more streamlined pathway for computing compact analytic results. Moreover, we present some recursive structures in these integral forms that show many of these expressions are interrelated. Key to our approach is that we are able to apply the minimal polynomial for a Lie algebra quite early in the process to keep expressions compact throughout the derivations. With the series approach, the minimal polynomial is usually applied at the end, making it hard to recognize common analytic expressions in the result. We show that our integral method can reproduce several series-derived results from the literature.

Certifiably Optimal Rotation and Pose Estimation Based on the Cayley Map

We present novel, tight, convex relaxations for rotation and pose estimation problems that can guarantee global optimality via strong Lagrangian duality. Some such relaxations exist in the literature for specific problem setups that assume the matrix von Mises-Fisher distribution (a.k.a., matrix Langevin distribution or chordal distance) for isotropic rotational uncertainty. However, another common way to represent uncertainty for rotations and poses is to define anisotropic noise in the associated Lie algebra. Starting from a noise model based on the Cayley map, we define our estimation problems, convert them to Quadratically Constrained Quadratic Programs (QCQPs), then relax them to Semidefinite Programs (SDPs), which can be solved using standard interior-point optimization methods. We first show how to carry out basic rotation and pose averaging. We then turn to the more complex problem of trajectory estimation, which involves many pose variables with both individual and inter-pose measurements (or motion priors). Our contribution is to formulate SDP relaxations for all these problems, including the identification of sufficient redundant constraints to make them tight. We hope our results can add to the catalogue of useful estimation problems whose global optimality can be guaranteed.

On Semidefinite Relaxations for Matrix-Weighted State-Estimation Problems in Robotics

In recent years, there has been remarkable progress in the development of so-called certifiable perception methods, which leverage semidefinite, convex relaxations to find global optima of perception problems in robotics. However, many of these relaxations rely on simplifying assumptions that facilitate the problem formulation, such as an isotropic measurement noise distribution. In this paper, we explore the tightness of the semidefinite relaxations of matrix-weighted (anisotropic) state-estimation problems and reveal the limitations lurking therein: matrix-weighted factors can cause convex relaxations to lose tightness. In particular, we show that the semidefinite relaxations of localization problems with matrix weights may be tight only for low noise levels. We empirically explore the factors that contribute to this loss of tightness and demonstrate that redundant constraints can be used to regain tightness, albeit at the expense of real-time performance. As a second technical contribution of this paper, we show that the state-of-the-art relaxation of scalar-weighted SLAM cannot be used when matrix weights are considered. We provide an alternate formulation and show that its SDP relaxation is not tight (even for very low noise levels) unless specific redundant constraints are used. We demonstrate the tightness of our formulations on both simulated and real-world data.

A Fine Line: Total Least-Squares Line Fitting as QCQP Optimization

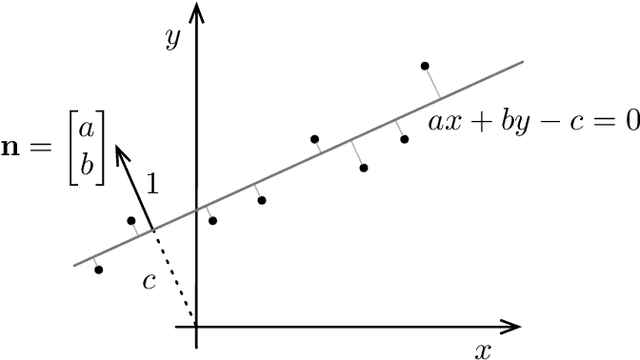
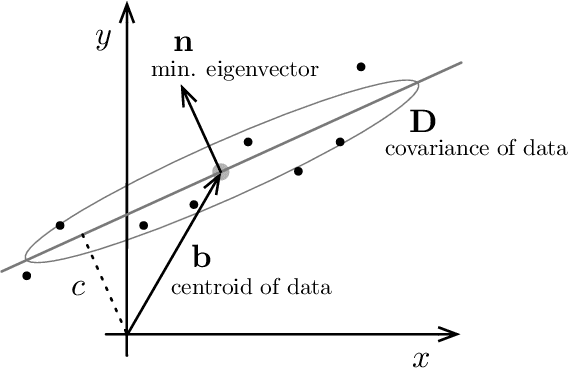
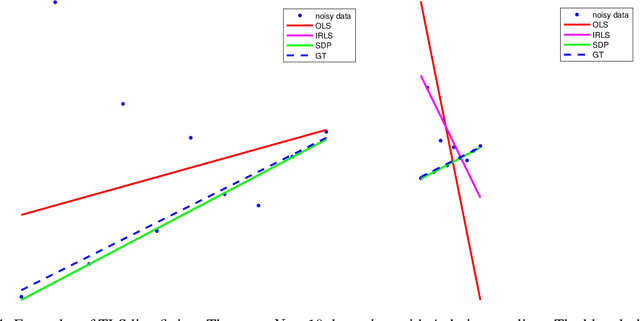
This note uses the Total Least-Squares (TLS) line-fitting problem as a canvas to explore some modern optimization tools. The contribution is meant to be tutorial in nature. The TLS problem has a lot of mathematical similarities to important problems in robotics and computer vision but is easier to visualize and understand. We demonstrate how to turn this problem into a Quadratically Constrained Quadratic Program (QCQP) so that it can be cast either as an eigenproblem or a Semi-Definite Program (SDP). We then turn to the more challenging situation where a Geman-McClure cost function and M-estimation are used to reject outlier datapoints. Using Black-Rangarajan duality, we show this can also be cast as a QCQP and solved as an SDP; however, with a lot of data the SDP can be slow and as such we show how we can construct a certificate of optimality for a faster method such as Iteratively Reweighted Least-Squares (IRLS).

On the Eigenstructure of Rotations and Poses: Commonalities and Peculiarities

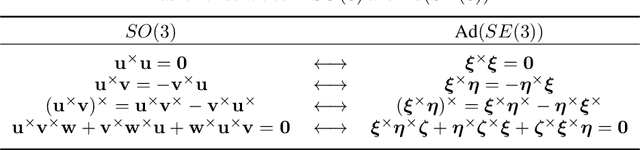
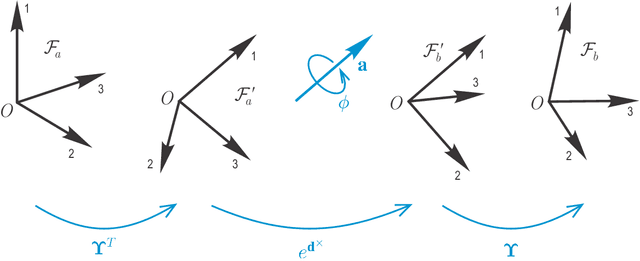
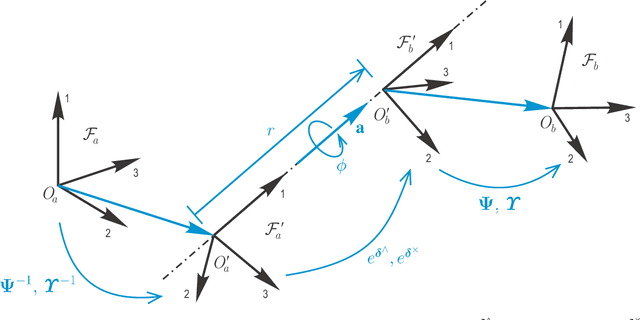
Rotations and poses are ubiquitous throughout many fields of science and engineering such as robotics, aerospace, computer vision and graphics. In this paper, we provide a complete characterization of rotations and poses in terms of the eigenstructure of their matrix Lie group representations, SO(3), SE(3) and Ad(SE(3)). An eigendecomposition of the pose representations reveals that they can be cast into a form very similar to that of rotations although the structure of the former can vary depending on the relative nature of the translation and rotation involved. Understanding the eigenstructure of these important quantities has merit in and of itself but it is also essential to appreciating such practical results as the minimal polynomial for rotations and poses and the calculation of Jacobians; moreover, we can speak of a principal-axis pose in much the same manner that we can of a principal-axis rotation.

A Geometric Algebra Solution to Wahba's Problem

We retrace Davenport's solution to Wahba's classic problem of aligning two pointclouds using the formalism of Geometric Algebra (GA). GA proves to be a natural backdrop for this problem involving three-dimensional rotations due to the isomorphism between unit-length quaternions and rotors. While the solution to this problem is not a new result, it is hoped that its treatment in GA will have tutorial value as well as open the door to addressing more complex problems in a similar way.

Fundamental Linear Algebra Problem of Gaussian Inference

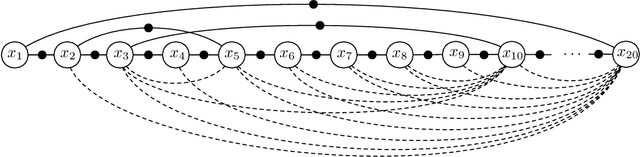
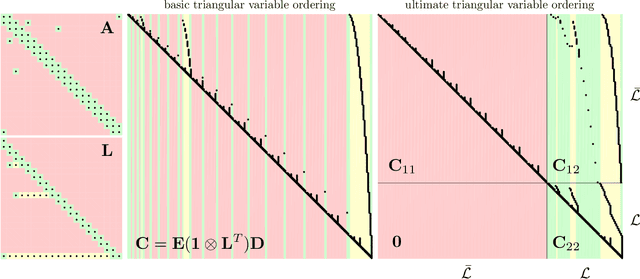
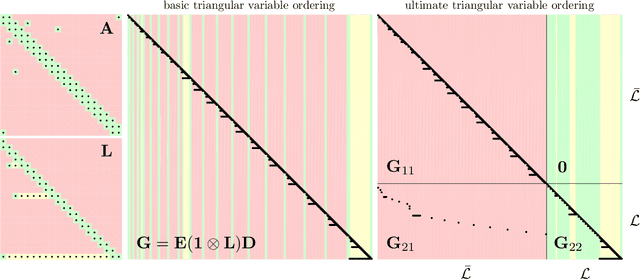
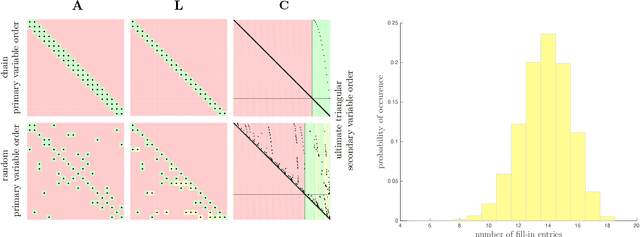
Underlying many Bayesian inference techniques that seek to approximate the posterior as a Gaussian distribution is a fundamental linear algebra problem that must be solved for both the mean and key entries of the covariance. Even when the true posterior is not Gaussian (e.g., in the case of nonlinear measurement functions) we can use variational schemes that repeatedly solve this linear algebra problem at each iteration. In most cases, the question is not whether a solution to this problem exists, but rather how we can exploit problem-specific structure to find it efficiently. Our contribution is to clearly state the Fundamental Linear Algebra Problem of Gaussian Inference (FLAPOGI) and to provide a novel presentation (using Kronecker algebra) of the not-so-well-known result of Takahashi et al. (1973) that makes it possible to solve for key entries of the covariance matrix. We first provide a global solution and then a local version that can be implemented using local message passing amongst a collection of agents calculating in parallel. Contrary to belief propagation, our local scheme is guaranteed to converge in both the mean and desired covariance quantities to the global solution even when the underlying factor graph is loopy; in the case of synchronous updates, we provide a bound on the number of iterations required for convergence. Compared to belief propagation, this guaranteed convergence comes at the cost of additional storage, calculations, and communication links in the case of loops; however, we show how these can be automatically constructed on the fly using only local information.

Informed Sampling for Asymptotically Optimal Path Planning (Consolidated Version)

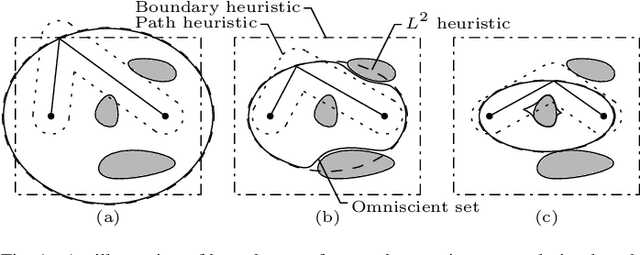
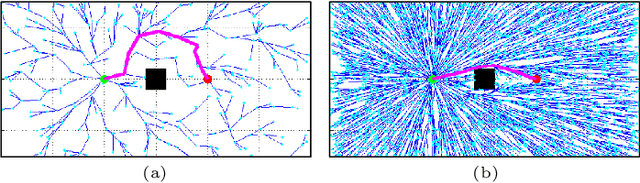
Anytime almost-surely asymptotically optimal planners, such as RRT*, incrementally find paths to every state in the search domain. This is inefficient once an initial solution is found as then only states that can provide a better solution need to be considered. Exact knowledge of these states requires solving the problem but can be approximated with heuristics. This paper formally defines these sets of states and demonstrates how they can be used to analyze arbitrary planning problems. It uses the well-known $L^2$ norm (i.e., Euclidean distance) to analyze minimum-path-length problems and shows that existing approaches decrease in effectiveness factorially (i.e., faster than exponentially) with state dimension. It presents a method to address this curse of dimensionality by directly sampling the prolate hyperspheroids (i.e., symmetric $n$-dimensional ellipses) that define the $L^2$ informed set. The importance of this direct informed sampling technique is demonstrated with Informed RRT*. This extension of RRT* has less theoretical dependence on state dimension and problem size than existing techniques and allows for linear convergence on some problems. It is shown experimentally to find better solutions faster than existing techniques on both abstract planning problems and HERB, a two-arm manipulation robot.