Fundamental Linear Algebra Problem of Gaussian Inference
Paper and Code
Oct 15, 2020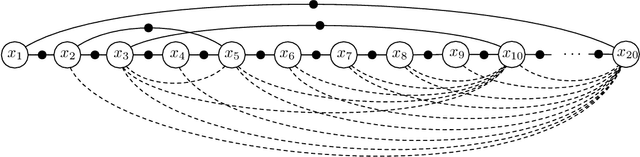
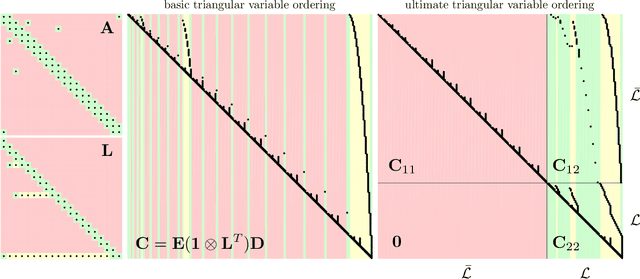
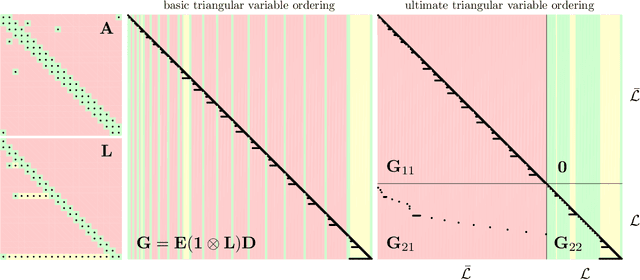
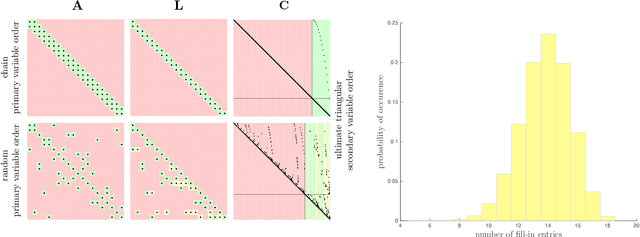
Underlying many Bayesian inference techniques that seek to approximate the posterior as a Gaussian distribution is a fundamental linear algebra problem that must be solved for both the mean and key entries of the covariance. Even when the true posterior is not Gaussian (e.g., in the case of nonlinear measurement functions) we can use variational schemes that repeatedly solve this linear algebra problem at each iteration. In most cases, the question is not whether a solution to this problem exists, but rather how we can exploit problem-specific structure to find it efficiently. Our contribution is to clearly state the Fundamental Linear Algebra Problem of Gaussian Inference (FLAPOGI) and to provide a novel presentation (using Kronecker algebra) of the not-so-well-known result of Takahashi et al. (1973) that makes it possible to solve for key entries of the covariance matrix. We first provide a global solution and then a local version that can be implemented using local message passing amongst a collection of agents calculating in parallel. Contrary to belief propagation, our local scheme is guaranteed to converge in both the mean and desired covariance quantities to the global solution even when the underlying factor graph is loopy; in the case of synchronous updates, we provide a bound on the number of iterations required for convergence. Compared to belief propagation, this guaranteed convergence comes at the cost of additional storage, calculations, and communication links in the case of loops; however, we show how these can be automatically constructed on the fly using only local information.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge