A Fine Line: Total Least-Squares Line Fitting as QCQP Optimization

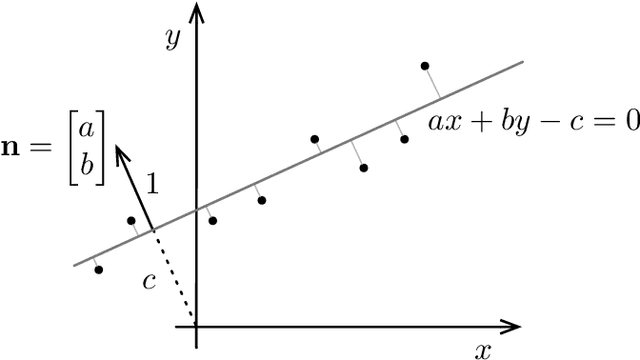
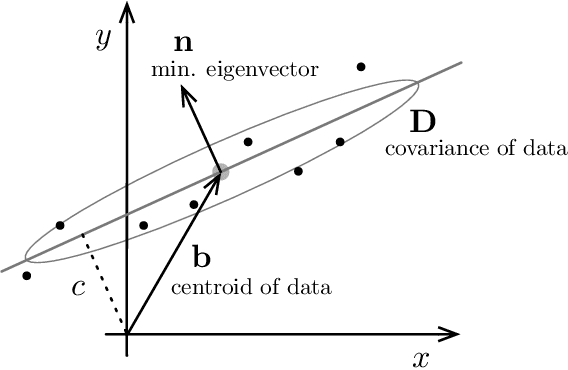
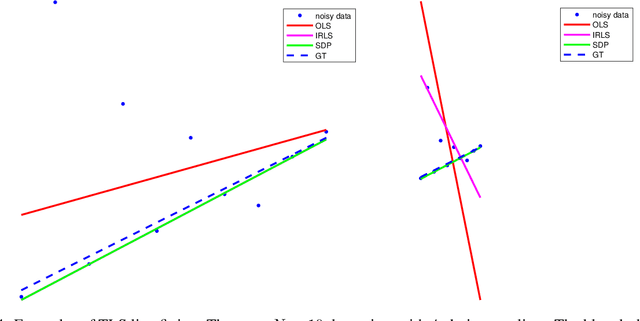
This note uses the Total Least-Squares (TLS) line-fitting problem as a canvas to explore some modern optimization tools. The contribution is meant to be tutorial in nature. The TLS problem has a lot of mathematical similarities to important problems in robotics and computer vision but is easier to visualize and understand. We demonstrate how to turn this problem into a Quadratically Constrained Quadratic Program (QCQP) so that it can be cast either as an eigenproblem or a Semi-Definite Program (SDP). We then turn to the more challenging situation where a Geman-McClure cost function and M-estimation are used to reject outlier datapoints. Using Black-Rangarajan duality, we show this can also be cast as a QCQP and solved as an SDP; however, with a lot of data the SDP can be slow and as such we show how we can construct a certificate of optimality for a faster method such as Iteratively Reweighted Least-Squares (IRLS).