Informed Sampling for Asymptotically Optimal Path Planning (Consolidated Version)
Paper and Code
Aug 17, 2018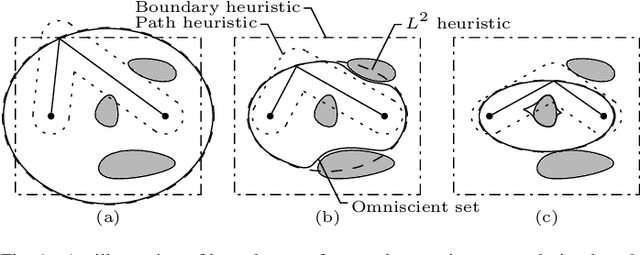
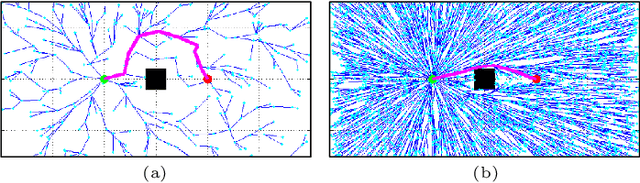
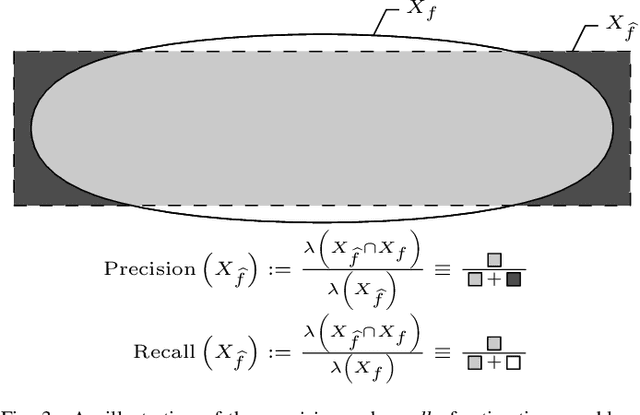

Anytime almost-surely asymptotically optimal planners, such as RRT*, incrementally find paths to every state in the search domain. This is inefficient once an initial solution is found as then only states that can provide a better solution need to be considered. Exact knowledge of these states requires solving the problem but can be approximated with heuristics. This paper formally defines these sets of states and demonstrates how they can be used to analyze arbitrary planning problems. It uses the well-known $L^2$ norm (i.e., Euclidean distance) to analyze minimum-path-length problems and shows that existing approaches decrease in effectiveness factorially (i.e., faster than exponentially) with state dimension. It presents a method to address this curse of dimensionality by directly sampling the prolate hyperspheroids (i.e., symmetric $n$-dimensional ellipses) that define the $L^2$ informed set. The importance of this direct informed sampling technique is demonstrated with Informed RRT*. This extension of RRT* has less theoretical dependence on state dimension and problem size than existing techniques and allows for linear convergence on some problems. It is shown experimentally to find better solutions faster than existing techniques on both abstract planning problems and HERB, a two-arm manipulation robot.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge