An Algebraic View of the Expressivity of Recurrent Language Models

What formal languages can a recurrent neural language model recognize? Formal results in the literature conflict: some authors report Turing-completeness, while others show equivalence to regular languages. The reason for this discrepancy is that the underlying arithmetic model differs. The paper develops a unified algebraic account of the expressivity of recurrent neural networks, starting with a formal account of various arithmetic models. This account reduces expressivity to an algebraic question, e.g., whether a network's syntactic monoid divides a certain wreath product. As a case study, the paper revisits diagonal state-space models: the same architecture cannot implement an even-modulus counter once floating-point recurrences are enforced, yet realizes every even-modulus counter under unsigned-integer quantization.

The Harmonic Structure of Information Contours

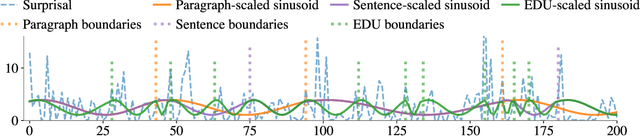
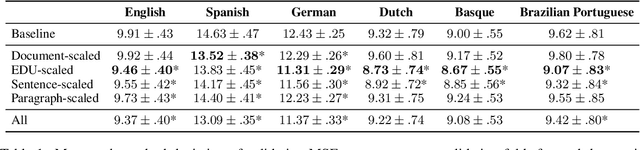
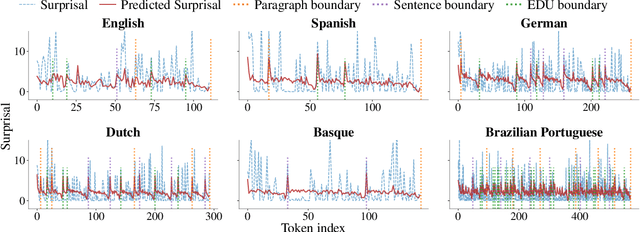
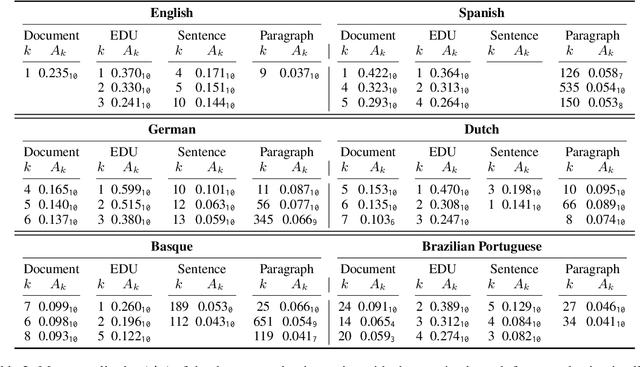
The uniform information density (UID) hypothesis proposes that speakers aim to distribute information evenly throughout a text, balancing production effort and listener comprehension difficulty. However, language typically does not maintain a strictly uniform information rate; instead, it fluctuates around a global average. These fluctuations are often explained by factors such as syntactic constraints, stylistic choices, or audience design. In this work, we explore an alternative perspective: that these fluctuations may be influenced by an implicit linguistic pressure towards periodicity, where the information rate oscillates at regular intervals, potentially across multiple frequencies simultaneously. We apply harmonic regression and introduce a novel extension called time scaling to detect and test for such periodicity in information contours. Analyzing texts in English, Spanish, German, Dutch, Basque, and Brazilian Portuguese, we find consistent evidence of periodic patterns in information rate. Many dominant frequencies align with discourse structure, suggesting these oscillations reflect meaningful linguistic organization. Beyond highlighting the connection between information rate and discourse structure, our approach offers a general framework for uncovering structural pressures at various levels of linguistic granularity.

An $\mathbf{L^*}$ Algorithm for Deterministic Weighted Regular Languages

Extracting finite state automata (FSAs) from black-box models offers a powerful approach to gaining interpretable insights into complex model behaviors. To support this pursuit, we present a weighted variant of Angluin's (1987) $\mathbf{L^*}$ algorithm for learning FSAs. We stay faithful to the original algorithm, devising a way to exactly learn deterministic weighted FSAs whose weights support division. Furthermore, we formulate the learning process in a manner that highlights the connection with FSA minimization, showing how $\mathbf{L^*}$ directly learns a minimal automaton for the target language.

Surprise! Uniform Information Density Isn't the Whole Story: Predicting Surprisal Contours in Long-form Discourse

The Uniform Information Density (UID) hypothesis posits that speakers tend to distribute information evenly across linguistic units to achieve efficient communication. Of course, information rate in texts and discourses is not perfectly uniform. While these fluctuations can be viewed as theoretically uninteresting noise on top of a uniform target, another explanation is that UID is not the only functional pressure regulating information content in a language. Speakers may also seek to maintain interest, adhere to writing conventions, and build compelling arguments. In this paper, we propose one such functional pressure; namely that speakers modulate information rate based on location within a hierarchically-structured model of discourse. We term this the Structured Context Hypothesis and test it by predicting the surprisal contours of naturally occurring discourses extracted from large language models using predictors derived from discourse structure. We find that hierarchical predictors are significant predictors of a discourse's information contour and that deeply nested hierarchical predictors are more predictive than shallow ones. This work takes an initial step beyond UID to propose testable hypotheses for why the information rate fluctuates in predictable ways

On the Representational Capacity of Neural Language Models with Chain-of-Thought Reasoning

The performance of modern language models (LMs) has been improved by chain-of-thought (CoT) reasoning, i.e., the process of generating intermediate results that guide the model towards a final answer. A possible explanation for this improvement is that CoT reasoning extends an LM's computational power, as RNNs and transformers with additional scratch space are known to be Turing complete. Comparing LMs to Turing machines, however, introduces a category error - Turing machines decide language membership, whereas LMs define distributions over strings. To bridge this gap, we formalize CoT reasoning in a probabilistic setting. We present several results on the representational capacity of recurrent and transformer LMs with CoT reasoning, showing that they can represent the same family of distributions over strings as probabilistic Turing machines.

What Languages are Easy to Language-Model? A Perspective from Learning Probabilistic Regular Languages

What can large language models learn? By definition, language models (LM) are distributions over strings. Therefore, an intuitive way of addressing the above question is to formalize it as a matter of learnability of classes of distributions over strings. While prior work in this direction focused on assessing the theoretical limits, in contrast, we seek to understand the empirical learnability. Unlike prior empirical work, we evaluate neural LMs on their home turf-learning probabilistic languages-rather than as classifiers of formal languages. In particular, we investigate the learnability of regular LMs (RLMs) by RNN and Transformer LMs. We empirically test the learnability of RLMs as a function of various complexity parameters of the RLM and the hidden state size of the neural LM. We find that the RLM rank, which corresponds to the size of linear space spanned by the logits of its conditional distributions, and the expected length of sampled strings are strong and significant predictors of learnability for both RNNs and Transformers. Several other predictors also reach significance, but with differing patterns between RNNs and Transformers.

Lower Bounds on the Expressivity of Recurrent Neural Language Models

The recent successes and spread of large neural language models (LMs) call for a thorough understanding of their computational ability. Describing their computational abilities through LMs' \emph{representational capacity} is a lively area of research. However, investigation into the representational capacity of neural LMs has predominantly focused on their ability to \emph{recognize} formal languages. For example, recurrent neural networks (RNNs) with Heaviside activations are tightly linked to regular languages, i.e., languages defined by finite-state automata (FSAs). Such results, however, fall short of describing the capabilities of RNN \emph{language models} (LMs), which are definitionally \emph{distributions} over strings. We take a fresh look at the representational capacity of RNN LMs by connecting them to \emph{probabilistic} FSAs and demonstrate that RNN LMs with linearly bounded precision can express arbitrary regular LMs.

On the Representational Capacity of Recurrent Neural Language Models

This work investigates the computational expressivity of language models (LMs) based on recurrent neural networks (RNNs). Siegelmann and Sontag (1992) famously showed that RNNs with rational weights and hidden states and unbounded computation time are Turing complete. However, LMs define weightings over strings in addition to just (unweighted) language membership and the analysis of the computational power of RNN LMs (RLMs) should reflect this. We extend the Turing completeness result to the probabilistic case, showing how a rationally weighted RLM with unbounded computation time can simulate any probabilistic Turing machine (PTM). Since, in practice, RLMs work in real-time, processing a symbol at every time step, we treat the above result as an upper bound on the expressivity of RLMs. We also provide a lower bound by showing that under the restriction to real-time computation, such models can simulate deterministic real-time rational PTMs.