Training Neural Networks as Recognizers of Formal Languages

Characterizing the computational power of neural network architectures in terms of formal language theory remains a crucial line of research, as it describes lower and upper bounds on the reasoning capabilities of modern AI. However, when empirically testing these bounds, existing work often leaves a discrepancy between experiments and the formal claims they are meant to support. The problem is that formal language theory pertains specifically to recognizers: machines that receive a string as input and classify whether it belongs to a language. On the other hand, it is common to instead use proxy tasks that are similar in only an informal sense, such as language modeling or sequence-to-sequence transduction. We correct this mismatch by training and evaluating neural networks directly as binary classifiers of strings, using a general method that can be applied to a wide variety of languages. As part of this, we extend an algorithm recently proposed by Sn{\ae}bjarnarson et al. (2024) to do length-controlled sampling of strings from regular languages, with much better asymptotic time complexity than previous methods. We provide results on a variety of languages across the Chomsky hierarchy for three neural architectures: a simple RNN, an LSTM, and a causally-masked transformer. We find that the RNN and LSTM often outperform the transformer, and that auxiliary training objectives such as language modeling can help, although no single objective uniformly improves performance across languages and architectures. Our contributions will facilitate theoretically sound empirical testing of language recognition claims in future work. We have released our datasets as a benchmark called FLaRe (Formal Language Recognition), along with our code.

On the Representational Capacity of Neural Language Models with Chain-of-Thought Reasoning

The performance of modern language models (LMs) has been improved by chain-of-thought (CoT) reasoning, i.e., the process of generating intermediate results that guide the model towards a final answer. A possible explanation for this improvement is that CoT reasoning extends an LM's computational power, as RNNs and transformers with additional scratch space are known to be Turing complete. Comparing LMs to Turing machines, however, introduces a category error - Turing machines decide language membership, whereas LMs define distributions over strings. To bridge this gap, we formalize CoT reasoning in a probabilistic setting. We present several results on the representational capacity of recurrent and transformer LMs with CoT reasoning, showing that they can represent the same family of distributions over strings as probabilistic Turing machines.

Efficient Algorithms for Recognizing Weighted Tree-Adjoining Languages

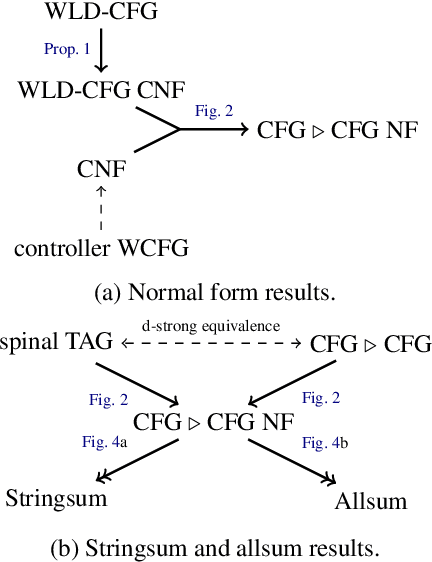
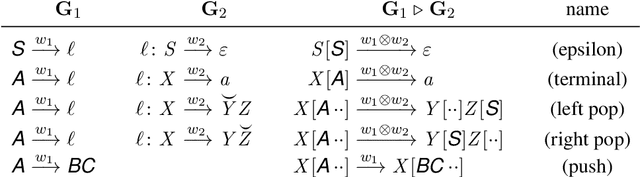
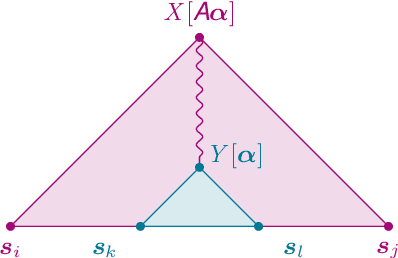
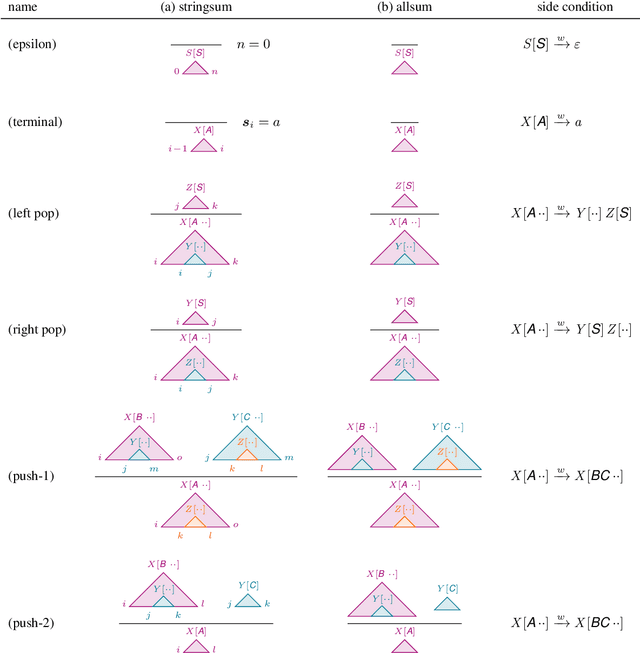
The class of tree-adjoining languages can be characterized by various two-level formalisms, consisting of a context-free grammar (CFG) or pushdown automaton (PDA) controlling another CFG or PDA. These four formalisms are equivalent to tree-adjoining grammars (TAG), linear indexed grammars (LIG), pushdown-adjoining automata (PAA), and embedded pushdown automata (EPDA). We define semiring-weighted versions of the above two-level formalisms, and we design new algorithms for computing their stringsums (the weight of all derivations of a string) and allsums (the weight of all derivations). From these, we also immediately obtain stringsum and allsum algorithms for TAG, LIG, PAA, and EPDA. For LIG, our algorithm is more time-efficient by a factor of $\mathcal{O}(n|\mathcal{N}|)$ (where $n$ is the string length and $|\mathcal{N}|$ is the size of the nonterminal set) and more space-efficient by a factor of $\mathcal{O}(|\Gamma|)$ (where $|\Gamma|$ is the size of the stack alphabet) than the algorithm of Vijay-Shanker and Weir (1989). For EPDA, our algorithm is both more space-efficient and time-efficient than the algorithm of Alonso et al. (2001) by factors of $\mathcal{O}(|\Gamma|^2)$ and $\mathcal{O}(|\Gamma|^3)$, respectively. Finally, we give the first PAA stringsum and allsum algorithms.

Convergence and Diversity in the Control Hierarchy

Weir has defined a hierarchy of language classes whose second member ($\mathcal{L}_2$) is generated by tree-adjoining grammars (TAG), linear indexed grammars (LIG), combinatory categorial grammars, and head grammars. The hierarchy is obtained using the mechanism of control, and $\mathcal{L}_2$ is obtained using a context-free grammar (CFG) whose derivations are controlled by another CFG. We adapt Weir's definition of a controllable CFG to give a definition of controllable pushdown automata (PDAs). This yields three new characterizations of $\mathcal{L}_2$ as the class of languages generated by PDAs controlling PDAs, PDAs controlling CFGs, and CFGs controlling PDAs. We show that these four formalisms are not only weakly equivalent but equivalent in a stricter sense that we call d-weak equivalence. Furthermore, using an even stricter notion of equivalence called d-strong equivalence, we make precise the intuition that a CFG controlling a CFG is a TAG, a PDA controlling a PDA is an embedded PDA, and a PDA controlling a CFG is a LIG. The fourth member of this family, a CFG controlling a PDA, does not correspond to any formalism we know of, so we invent one and call it a Pushdown Adjoining Automaton.

Algorithms for Weighted Pushdown Automata

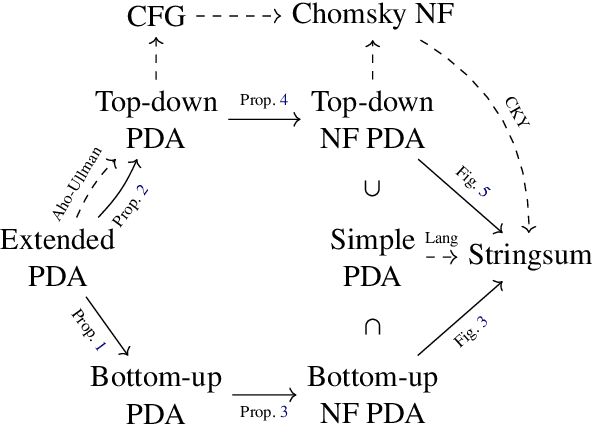
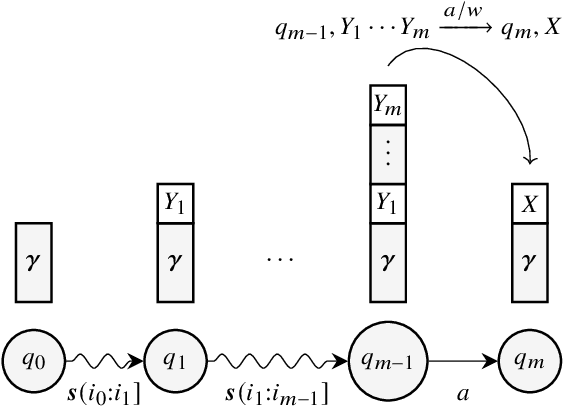
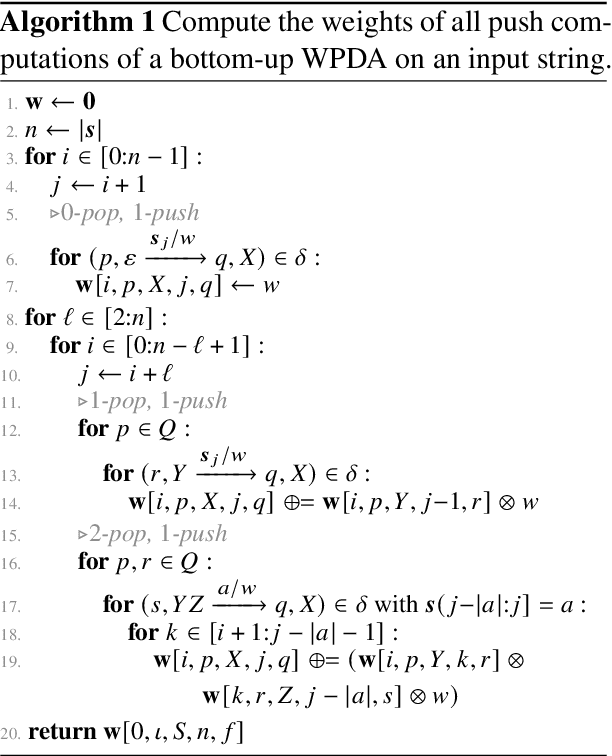
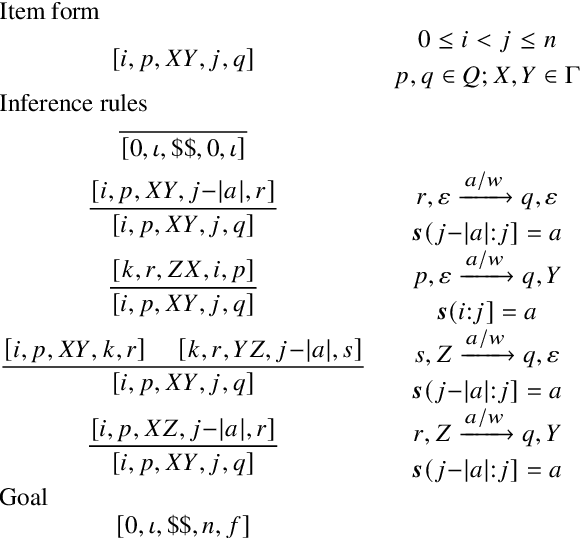
Weighted pushdown automata (WPDAs) are at the core of many natural language processing tasks, like syntax-based statistical machine translation and transition-based dependency parsing. As most existing dynamic programming algorithms are designed for context-free grammars (CFGs), algorithms for PDAs often resort to a PDA-to-CFG conversion. In this paper, we develop novel algorithms that operate directly on WPDAs. Our algorithms are inspired by Lang's algorithm, but use a more general definition of pushdown automaton and either reduce the space requirements by a factor of $|\Gamma|$ (the size of the stack alphabet) or reduce the runtime by a factor of more than $|Q|$ (the number of states). When run on the same class of PDAs as Lang's algorithm, our algorithm is both more space-efficient by a factor of $|\Gamma|$ and more time-efficient by a factor of $|Q| \cdot |\Gamma|$.