Algorithms for Weighted Pushdown Automata
Paper and Code
Oct 19, 2022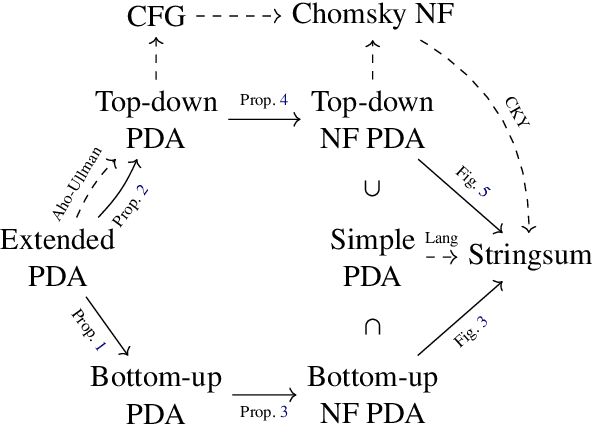
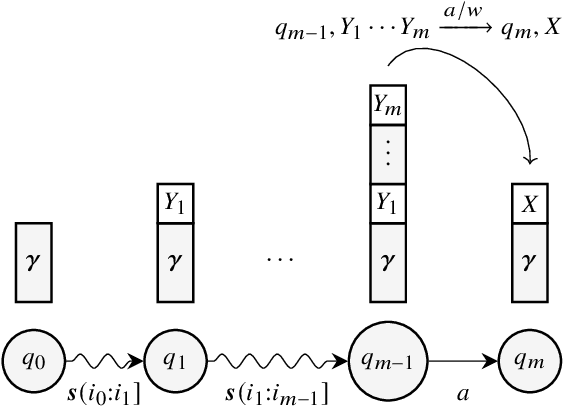
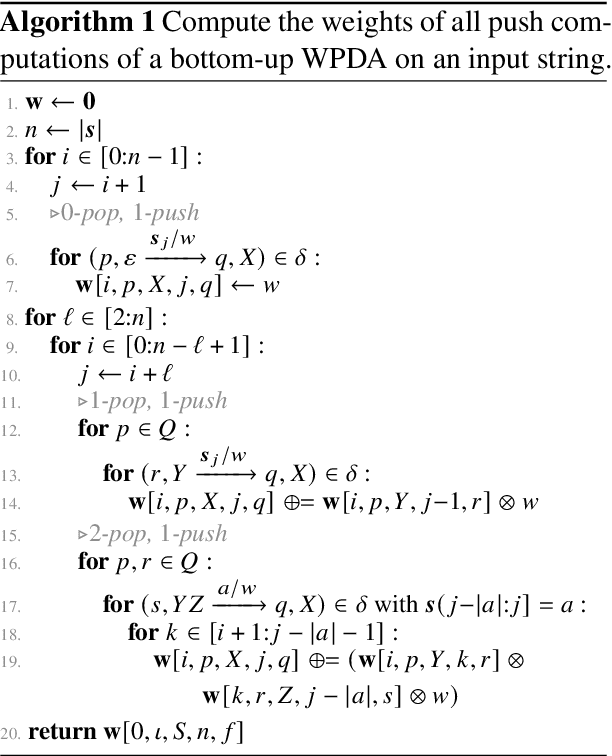
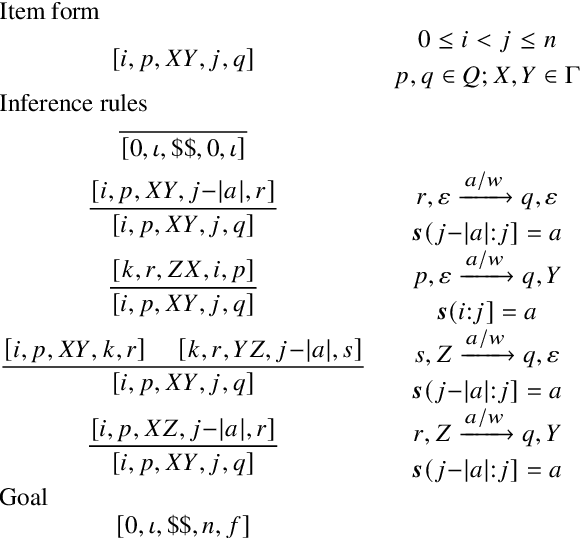
Weighted pushdown automata (WPDAs) are at the core of many natural language processing tasks, like syntax-based statistical machine translation and transition-based dependency parsing. As most existing dynamic programming algorithms are designed for context-free grammars (CFGs), algorithms for PDAs often resort to a PDA-to-CFG conversion. In this paper, we develop novel algorithms that operate directly on WPDAs. Our algorithms are inspired by Lang's algorithm, but use a more general definition of pushdown automaton and either reduce the space requirements by a factor of $|\Gamma|$ (the size of the stack alphabet) or reduce the runtime by a factor of more than $|Q|$ (the number of states). When run on the same class of PDAs as Lang's algorithm, our algorithm is both more space-efficient by a factor of $|\Gamma|$ and more time-efficient by a factor of $|Q| \cdot |\Gamma|$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge