An $\mathbf{L^*}$ Algorithm for Deterministic Weighted Regular Languages

Extracting finite state automata (FSAs) from black-box models offers a powerful approach to gaining interpretable insights into complex model behaviors. To support this pursuit, we present a weighted variant of Angluin's (1987) $\mathbf{L^*}$ algorithm for learning FSAs. We stay faithful to the original algorithm, devising a way to exactly learn deterministic weighted FSAs whose weights support division. Furthermore, we formulate the learning process in a manner that highlights the connection with FSA minimization, showing how $\mathbf{L^*}$ directly learns a minimal automaton for the target language.

On Affine Homotopy between Language Encoders

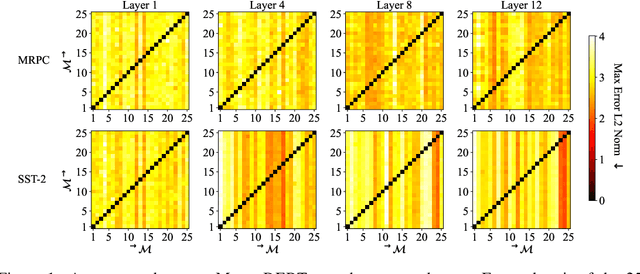
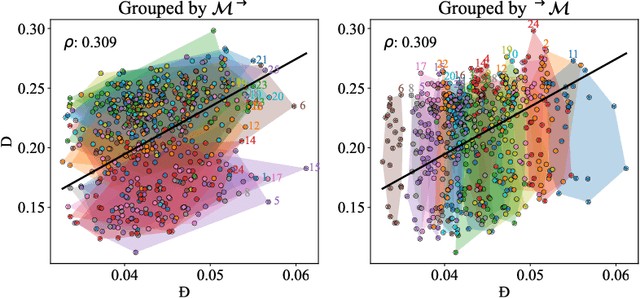
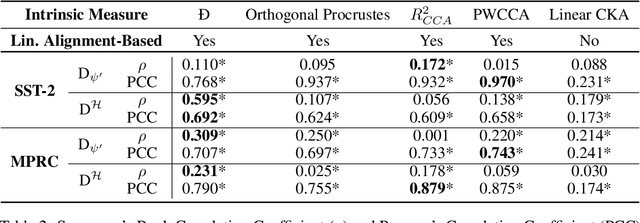
Pre-trained language encoders -- functions that represent text as vectors -- are an integral component of many NLP tasks. We tackle a natural question in language encoder analysis: What does it mean for two encoders to be similar? We contend that a faithful measure of similarity needs to be \emph{intrinsic}, that is, task-independent, yet still be informative of \emph{extrinsic} similarity -- the performance on downstream tasks. It is common to consider two encoders similar if they are \emph{homotopic}, i.e., if they can be aligned through some transformation. In this spirit, we study the properties of \emph{affine} alignment of language encoders and its implications on extrinsic similarity. We find that while affine alignment is fundamentally an asymmetric notion of similarity, it is still informative of extrinsic similarity. We confirm this on datasets of natural language representations. Beyond providing useful bounds on extrinsic similarity, affine intrinsic similarity also allows us to begin uncovering the structure of the space of pre-trained encoders by defining an order over them.