Adaptive Least Mean pth Power Graph Neural Networks

In the presence of impulsive noise, and missing observations, accurate online prediction of time-varying graph signals poses a crucial challenge in numerous application domains. We propose the Adaptive Least Mean $p^{th}$ Power Graph Neural Networks (LMP-GNN), a universal framework combining adaptive filter and graph neural network for online graph signal estimation. LMP-GNN retains the advantage of adaptive filtering in handling noise and missing observations as well as the online update capability. The incorporated graph neural network within the LMP-GNN can train and update filter parameters online instead of predefined filter parameters in previous methods, outputting more accurate prediction results. The adaptive update scheme of the LMP-GNN follows the solution of a $l_p$-norm optimization, rooting to the minimum dispersion criterion, and yields robust estimation results for time-varying graph signals under impulsive noise. A special case of LMP-GNN named the Sign-GNN is also provided and analyzed, Experiment results on two real-world datasets of temperature graph and traffic graph under four different noise distributions prove the effectiveness and robustness of our proposed LMP-GNN.

Binarized Simplicial Convolutional Neural Networks

Graph Neural Networks have a limitation of solely processing features on graph nodes, neglecting data on high-dimensional structures such as edges and triangles. Simplicial Convolutional Neural Networks (SCNN) represent higher-order structures using simplicial complexes to break this limitation albeit still lacking time efficiency. In this paper, we propose a novel neural network architecture on simplicial complexes named Binarized Simplicial Convolutional Neural Networks (Bi-SCNN) based on the combination of simplicial convolution with a binary-sign forward propagation strategy. The usage of the Hodge Laplacian on a binary-sign forward propagation enables Bi-SCNN to efficiently and effectively represent simplicial features that have higher-order structures than traditional graph node representations. Compared to the previous Simplicial Convolutional Neural Networks, the reduced model complexity of Bi-SCNN shortens the execution time without sacrificing the prediction performance and is less prone to the over-smoothing effect. Experimenting with real-world citation and ocean-drifter data confirmed that our proposed Bi-SCNN is efficient and accurate.

Adaptive Graph Normalized Sign Algorithm

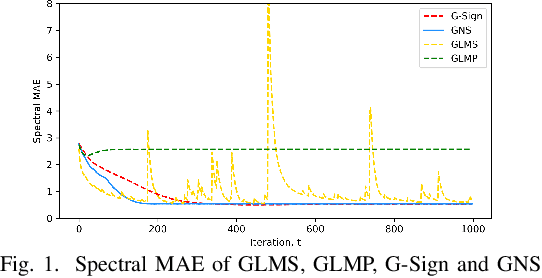
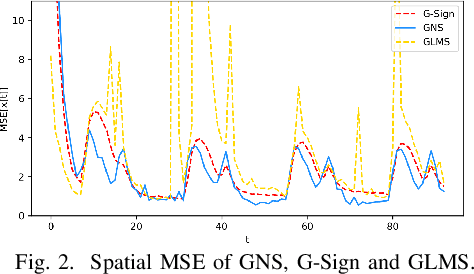
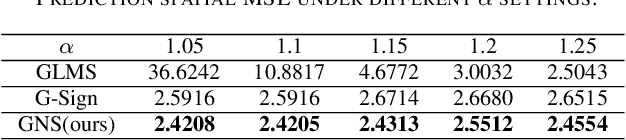
Efficient and robust prediction of graph signals is challenging when the signals are under impulsive noise and have missing data. Exploiting graph signal processing (GSP) and leveraging the simplicity of the classical adaptive sign algorithm, we propose an adaptive algorithm on graphs named the Graph Normalized Sign (GNS). GNS approximated a normalization term into the update, therefore achieving faster convergence and lower error compared to previous adaptive GSP algorithms. In the task of the online prediction of multivariate temperature data under impulsive noise, GNS outputs fast and robust predictions.

From Bandits Model to Deep Deterministic Policy Gradient, Reinforcement Learning with Contextual Information

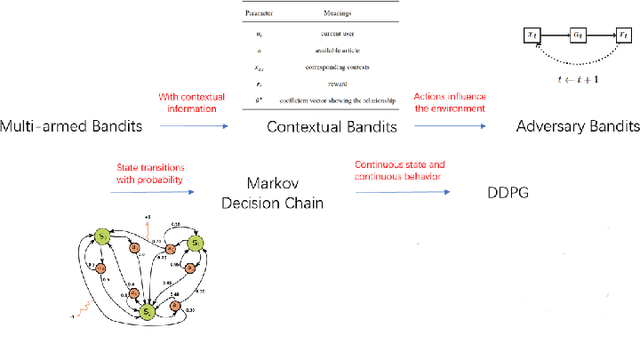
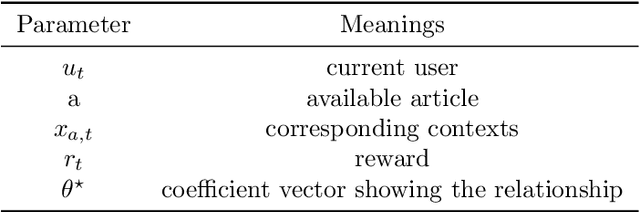
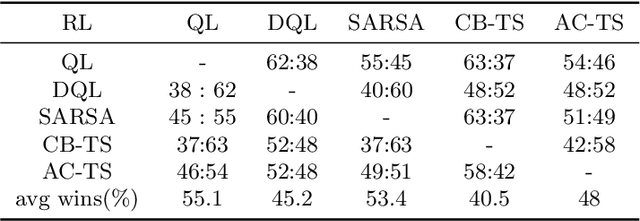
The problem of how to take the right actions to make profits in sequential process continues to be difficult due to the quick dynamics and a significant amount of uncertainty in many application scenarios. In such complicated environments, reinforcement learning (RL), a reward-oriented strategy for optimum control, has emerged as a potential technique to address this strategic decision-making issue. However, reinforcement learning also has some shortcomings that make it unsuitable for solving many financial problems, excessive resource consumption, and inability to quickly obtain optimal solutions, making it unsuitable for quantitative trading markets. In this study, we use two methods to overcome the issue with contextual information: contextual Thompson sampling and reinforcement learning under supervision which can accelerate the iterations in search of the best answer. In order to investigate strategic trading in quantitative markets, we merged the earlier financial trading strategy known as constant proportion portfolio insurance (CPPI) into deep deterministic policy gradient (DDPG). The experimental results show that both methods can accelerate the progress of reinforcement learning to obtain the optimal solution.

Strategic Trading in Quantitative Markets through Multi-Agent Reinforcement Learning

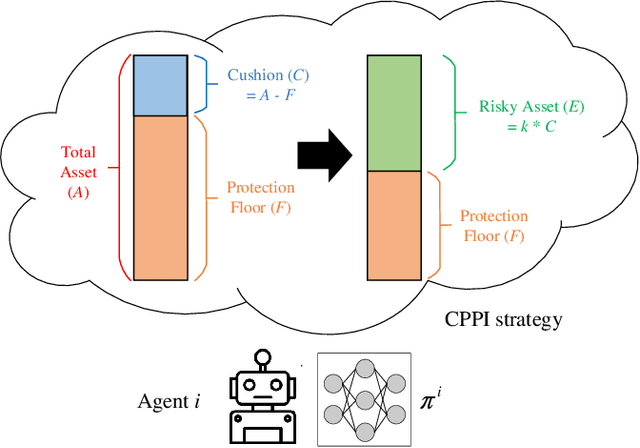
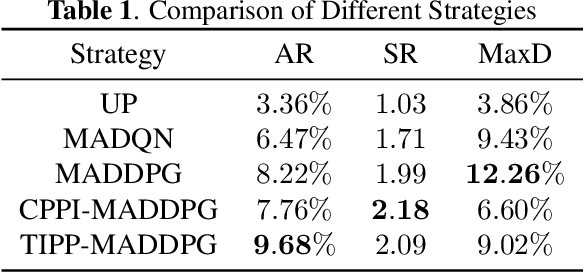
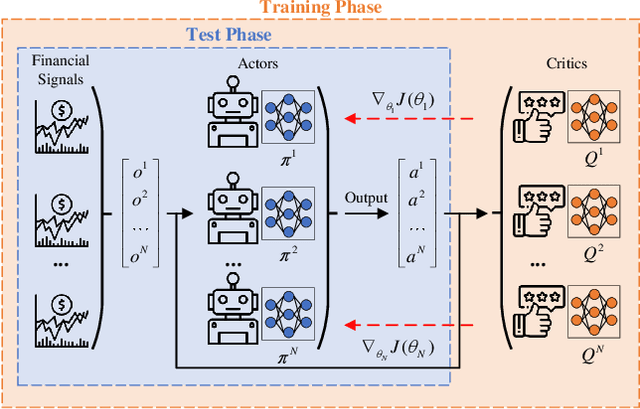
Due to the rapid dynamics and a mass of uncertainties in the quantitative markets, the issue of how to take appropriate actions to make profits in stock trading remains a challenging one. Reinforcement learning (RL), as a reward-oriented approach for optimal control, has emerged as a promising method to tackle this strategic decision-making problem in such a complex financial scenario. In this paper, we integrated two prior financial trading strategies named constant proportion portfolio insurance (CPPI) and time-invariant portfolio protection (TIPP) into multi-agent deep deterministic policy gradient (MADDPG) and proposed two specifically designed multi-agent RL (MARL) methods: CPPI-MADDPG and TIPP-MADDPG for investigating strategic trading in quantitative markets. Afterward, we selected 100 different shares in the real financial market to test these specifically proposed approaches. The experiment results show that CPPI-MADDPG and TIPP-MADDPG approaches generally outperform the conventional ones.

Joint online estimation of multi-order graph topological signals

In this paper, we propose a general method to process time-varying signals on different orders of simplicial complexes in an online fashion. The proposed Hodge normalized least mean square algorithm (Hodge-NLMS) utilizes spatial and spectral techniques of topological signal processing defined using the Hodge Laplacians to form an online algorithm for signals on either the nodes or the edges of a graph. The joint estimation of a graph with signals coexisting on nodes and edges is also realized through an alternating execution of the Hodge-NLMS on the nodes and edges. Experiment results have confirmed that our proposed methods could accurately track both time-varying node and edge signals on synthetic data generated on top of graphs collected in the real world.

Thompson Sampling on Asymmetric $α$-Stable Bandits

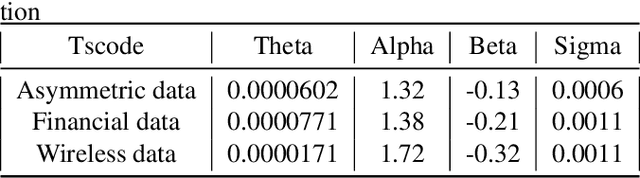
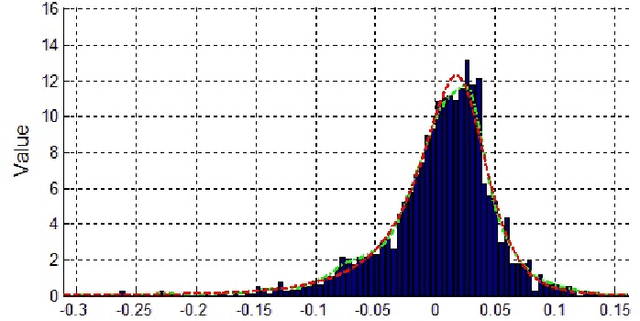
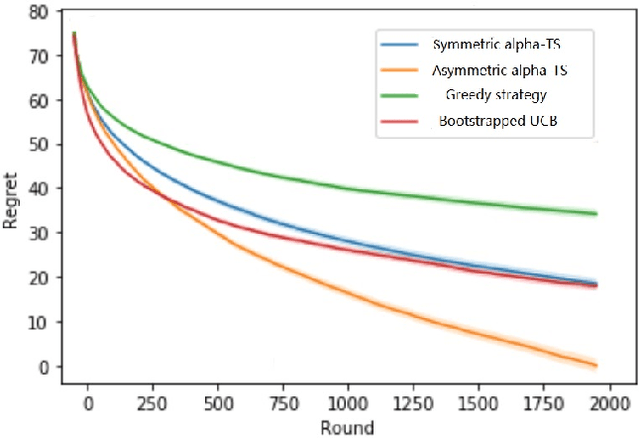
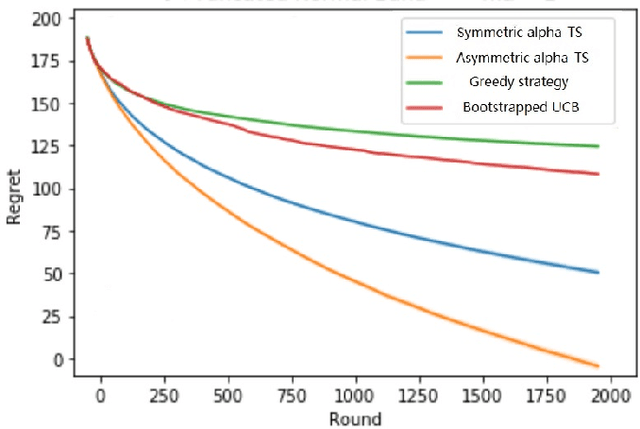
In algorithm optimization in reinforcement learning, how to deal with the exploration-exploitation dilemma is particularly important. Multi-armed bandit problem can optimize the proposed solutions by changing the reward distribution to realize the dynamic balance between exploration and exploitation. Thompson Sampling is a common method for solving multi-armed bandit problem and has been used to explore data that conform to various laws. In this paper, we consider the Thompson Sampling approach for multi-armed bandit problem, in which rewards conform to unknown asymmetric $\alpha$-stable distributions and explore their applications in modelling financial and wireless data.

Adaptive Sign Algorithm for Graph Signal Processing

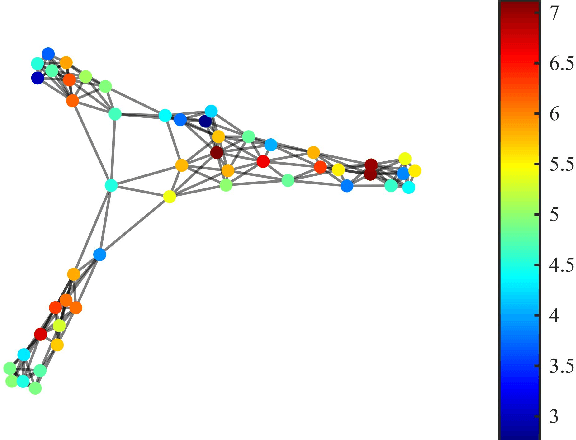
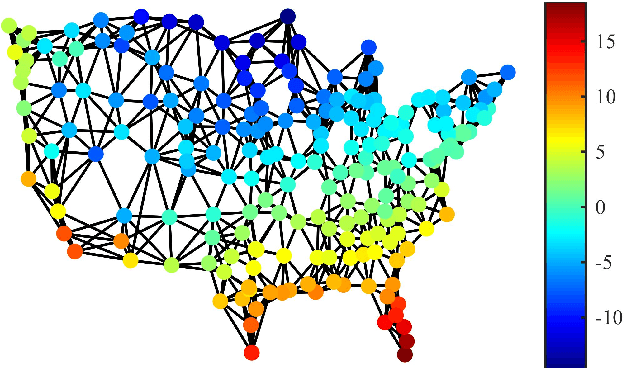
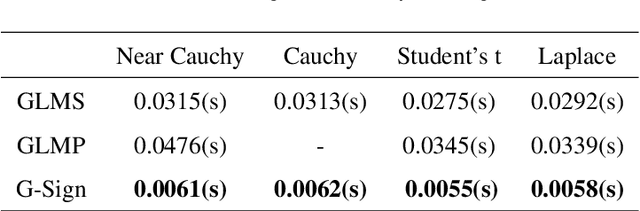
Efficient and robust online processing technique of irregularly structured data is crucial in the current era of data abundance. In this paper, we propose a graph/network version of the classical adaptive Sign algorithm for online graph signal estimation under impulsive noise. Recently introduced graph adaptive least mean squares algorithm is unstable under non-Gaussian impulsive noise and has high computational complexity. The Graph-Sign algorithm proposed in this work is based on the minimum dispersion criterion and therefore impulsive noise does not hinder its estimation quality. Unlike the recently proposed graph adaptive least mean p-th power algorithm, our Graph-Sign algorithm can operate without prior knowledge of the noise distribution. The proposed Graph-Sign algorithm has a faster run time because of its low computational complexity compared to the existing adaptive graph signal processing algorithms. Experimenting on steady-state and time-varying graph signals estimation utilizing spectral properties of bandlimitedness and sampling, the Graph-Sign algorithm demonstrates fast, stable, and robust graph signal estimation performance under impulsive noise modeled by alpha stable, Cauchy, Student's t, or Laplace distributions.

PAC-Bayes Information Bottleneck

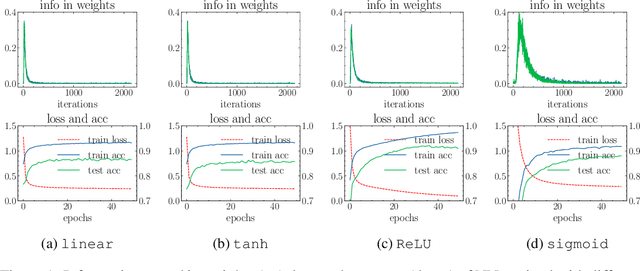
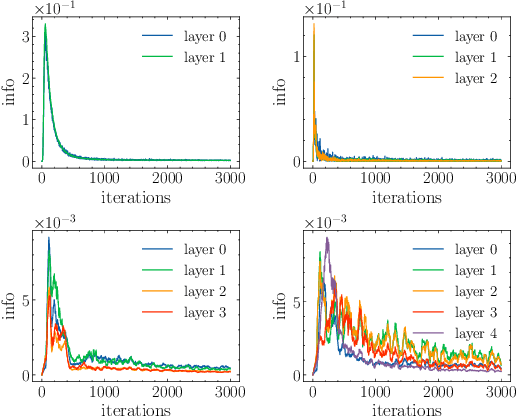
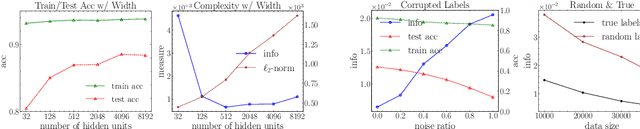
Information bottleneck (IB) depicts a trade-off between the accuracy and conciseness of encoded representations. IB has succeeded in explaining the objective and behavior of neural networks (NNs) as well as learning better representations. However, there are still critics of the universality of IB, e.g., phase transition usually fades away, representation compression is not causally related to generalization, and IB is trivial in deterministic cases. In this work, we build a new IB based on the trade-off between the accuracy and complexity of learned weights of NNs. We argue that this new IB represents a more solid connection to the objective of NNs since the information stored in weights (IIW) bounds their PAC-Bayes generalization capability, hence we name it as PAC-Bayes IB (PIB). On IIW, we can identify the phase transition phenomenon in general cases and solidify the causality between compression and generalization. We then derive a tractable solution of PIB and design a stochastic inference algorithm by Markov chain Monte Carlo sampling. We empirically verify our claims through extensive experiments. We also substantiate the superiority of the proposed algorithm on training NNs.

Information Theoretic Counterfactual Learning from Missing-Not-At-Random Feedback

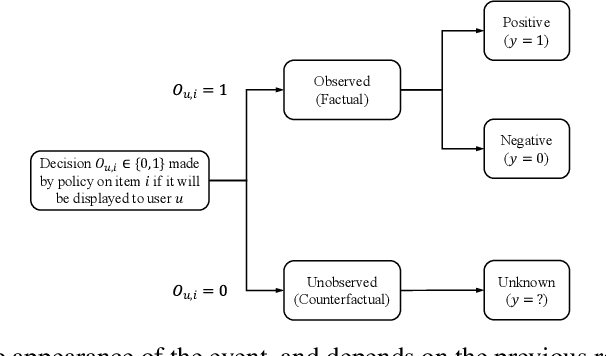
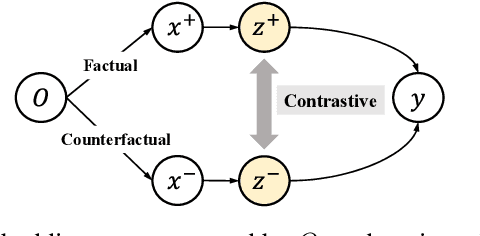
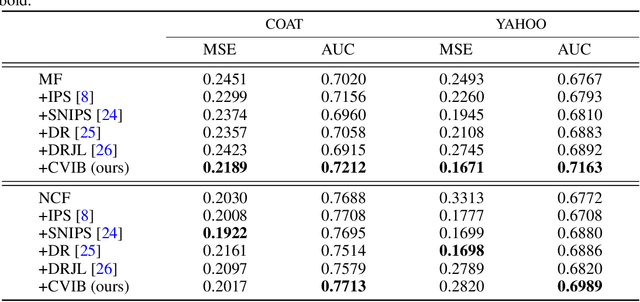
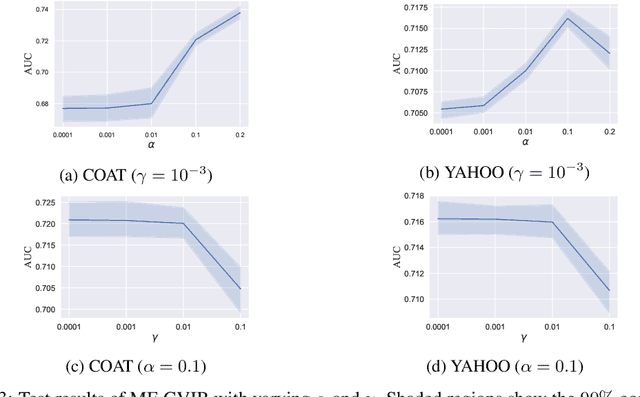
Counterfactual learning for dealing with missing-not-at-random data (MNAR) is an intriguing topic in the recommendation literature, since MNAR data are ubiquitous in modern recommender systems. Missing-at-random (MAR) data, namely randomized controlled trials (RCTs), are usually required by most previous counterfactual learning methods. However, the execution of RCTs is extraordinarily expensive in practice. To circumvent the use of RCTs, we build an information theoretic counterfactual variational information bottleneck (CVIB), as an alternative for debiasing learning without RCTs. By separating the task-aware mutual information term in the original information bottleneck Lagrangian into factual and counterfactual parts, we derive a contrastive information loss and an additional output confidence penalty, which facilitates balanced learning between the factual and counterfactual domains. Empirical evaluation on real-world datasets shows that our CVIB significantly enhances both shallow and deep models, which sheds light on counterfactual learning in recommendation that goes beyond RCTs.