Changran Peng
Graph Signal Adaptive Message Passing
Oct 23, 2024Abstract:This paper proposes Graph Signal Adaptive Message Passing (GSAMP), a novel message passing method that simultaneously conducts online prediction, missing data imputation, and noise removal on time-varying graph signals. Unlike conventional Graph Signal Processing methods that apply the same filter to the entire graph, the spatiotemporal updates of GSAMP employ a distinct approach that utilizes localized computations at each node. This update is based on an adaptive solution obtained from an optimization problem designed to minimize the discrepancy between observed and estimated values. GSAMP effectively processes real-world, time-varying graph signals under Gaussian and impulsive noise conditions.
Adaptive Graph Normalized Sign Algorithm
May 07, 2024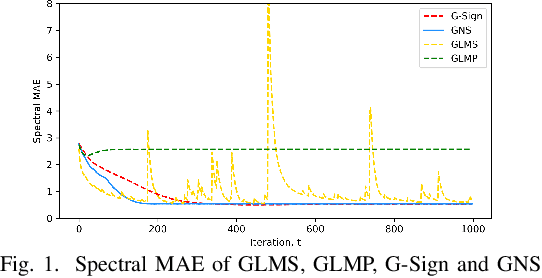
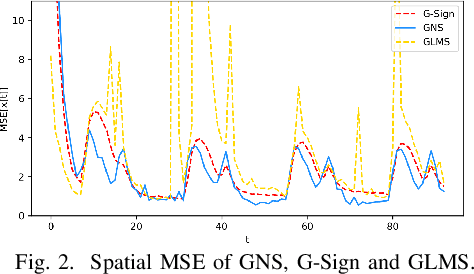
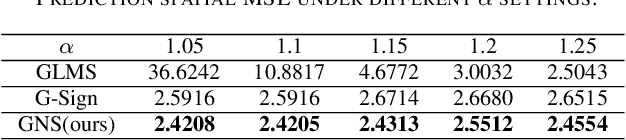
Abstract:Efficient and robust prediction of graph signals is challenging when the signals are under impulsive noise and have missing data. Exploiting graph signal processing (GSP) and leveraging the simplicity of the classical adaptive sign algorithm, we propose an adaptive algorithm on graphs named the Graph Normalized Sign (GNS). GNS approximated a normalization term into the update, therefore achieving faster convergence and lower error compared to previous adaptive GSP algorithms. In the task of the online prediction of multivariate temperature data under impulsive noise, GNS outputs fast and robust predictions.
Adaptive Least Mean pth Power Graph Neural Networks
May 07, 2024



Abstract:In the presence of impulsive noise, and missing observations, accurate online prediction of time-varying graph signals poses a crucial challenge in numerous application domains. We propose the Adaptive Least Mean $p^{th}$ Power Graph Neural Networks (LMP-GNN), a universal framework combining adaptive filter and graph neural network for online graph signal estimation. LMP-GNN retains the advantage of adaptive filtering in handling noise and missing observations as well as the online update capability. The incorporated graph neural network within the LMP-GNN can train and update filter parameters online instead of predefined filter parameters in previous methods, outputting more accurate prediction results. The adaptive update scheme of the LMP-GNN follows the solution of a $l_p$-norm optimization, rooting to the minimum dispersion criterion, and yields robust estimation results for time-varying graph signals under impulsive noise. A special case of LMP-GNN named the Sign-GNN is also provided and analyzed, Experiment results on two real-world datasets of temperature graph and traffic graph under four different noise distributions prove the effectiveness and robustness of our proposed LMP-GNN.
Adaptive Least Mean Squares Graph Neural Networks and Online Graph Signal Estimation
Jan 27, 2024Abstract:The online prediction of multivariate signals, existing simultaneously in space and time, from noisy partial observations is a fundamental task in numerous applications. We propose an efficient Neural Network architecture for the online estimation of time-varying graph signals named the Adaptive Least Mean Squares Graph Neural Networks (LMS-GNN). LMS-GNN aims to capture the time variation and bridge the cross-space-time interactions under the condition that signals are corrupted by noise and missing values. The LMS-GNN is a combination of adaptive graph filters and Graph Neural Networks (GNN). At each time step, the forward propagation of LMS-GNN is similar to adaptive graph filters where the output is based on the error between the observation and the prediction similar to GNN. The filter coefficients are updated via backpropagation as in GNN. Experimenting on real-world temperature data reveals that our LMS-GNN achieves more accurate online predictions compared to graph-based methods like adaptive graph filters and graph convolutional neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge