BrainNetMLP: An Efficient and Effective Baseline for Functional Brain Network Classification

Recent studies have made great progress in functional brain network classification by modeling the brain as a network of Regions of Interest (ROIs) and leveraging their connections to understand brain functionality and diagnose mental disorders. Various deep learning architectures, including Convolutional Neural Networks, Graph Neural Networks, and the recent Transformer, have been developed. However, despite the increasing complexity of these models, the performance gain has not been as salient. This raises a question: Does increasing model complexity necessarily lead to higher classification accuracy? In this paper, we revisit the simplest deep learning architecture, the Multi-Layer Perceptron (MLP), and propose a pure MLP-based method, named BrainNetMLP, for functional brain network classification, which capitalizes on the advantages of MLP, including efficient computation and fewer parameters. Moreover, BrainNetMLP incorporates a dual-branch structure to jointly capture both spatial connectivity and spectral information, enabling precise spatiotemporal feature fusion. We evaluate our proposed BrainNetMLP on two public and popular brain network classification datasets, the Human Connectome Project (HCP) and the Autism Brain Imaging Data Exchange (ABIDE). Experimental results demonstrate pure MLP-based methods can achieve state-of-the-art performance, revealing the potential of MLP-based models as more efficient yet effective alternatives in functional brain network classification. The code will be available at https://github.com/JayceonHo/BrainNetMLP.

ASD Classification on Dynamic Brain Connectome using Temporal Random Walk with Transformer-based Dynamic Network Embedding

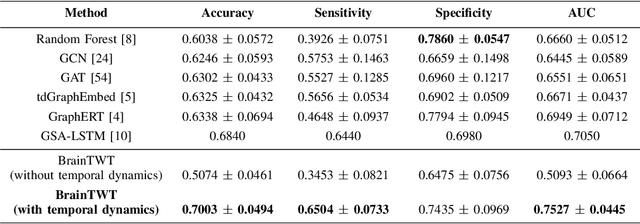
Autism Spectrum Disorder (ASD) is a complex neurological condition characterized by varied developmental impairments, especially in communication and social interaction. Accurate and early diagnosis of ASD is crucial for effective intervention, which is enhanced by richer representations of brain activity. The brain functional connectome, which refers to the statistical relationships between different brain regions measured through neuroimaging, provides crucial insights into brain function. Traditional static methods often fail to capture the dynamic nature of brain activity, in contrast, dynamic brain connectome analysis provides a more comprehensive view by capturing the temporal variations in the brain. We propose BrainTWT, a novel dynamic network embedding approach that captures temporal evolution of the brain connectivity over time and considers also the dynamics between different temporal network snapshots. BrainTWT employs temporal random walks to capture dynamics across different temporal network snapshots and leverages the Transformer's ability to model long term dependencies in sequential data to learn the discriminative embeddings from these temporal sequences using temporal structure prediction tasks. The experimental evaluation, utilizing the Autism Brain Imaging Data Exchange (ABIDE) dataset, demonstrates that BrainTWT outperforms baseline methods in ASD classification.

Spatio-Temporal Graph Structure Learning for Earthquake Detection

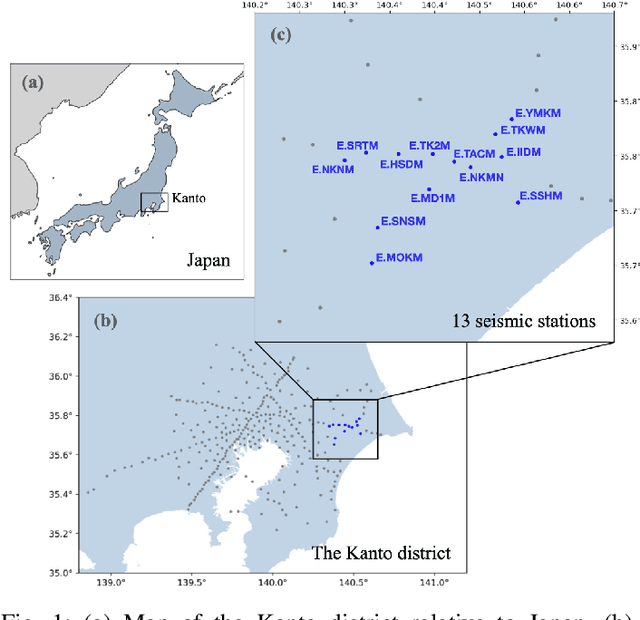
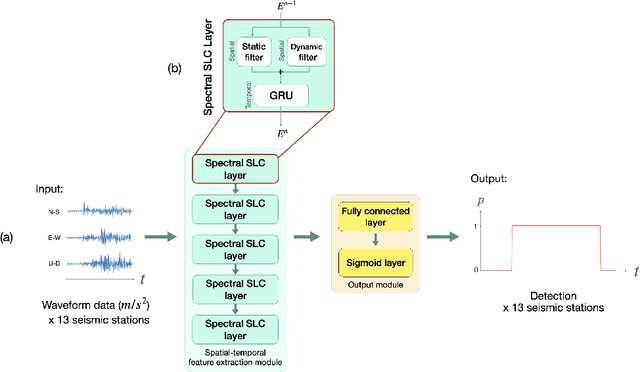
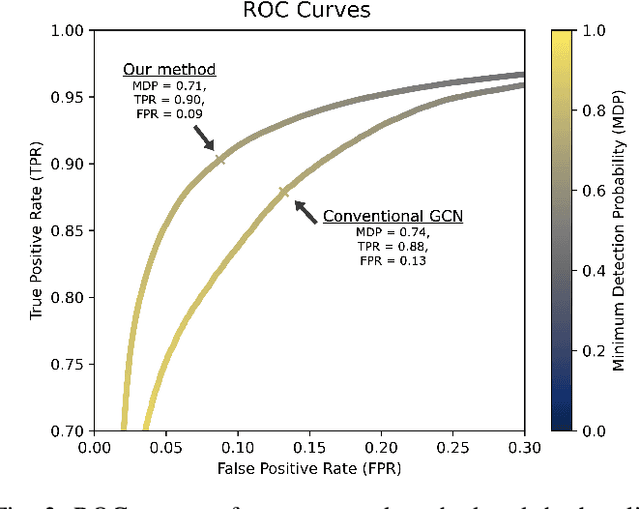
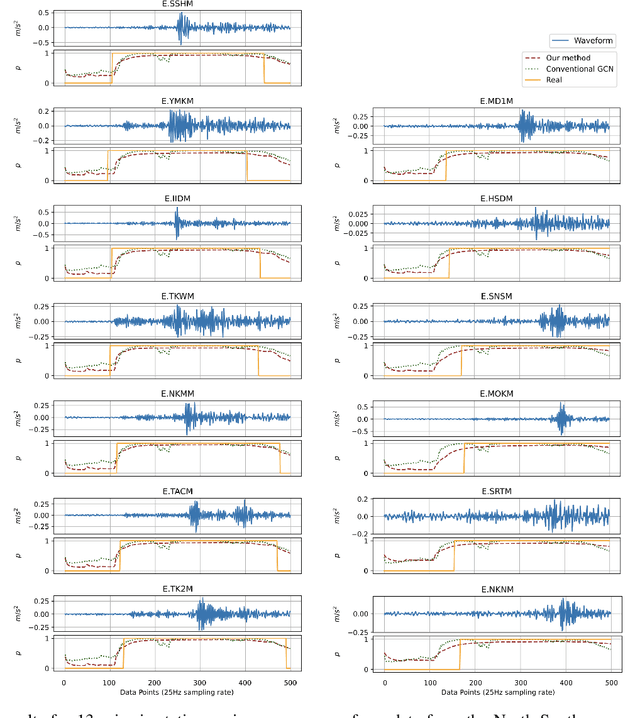
Earthquake detection is essential for earthquake early warning (EEW) systems. Traditional methods struggle with low signal-to-noise ratios and single-station reliance, limiting their effectiveness. We propose a Spatio-Temporal Graph Convolutional Network (GCN) using Spectral Structure Learning Convolution (Spectral SLC) to model static and dynamic relationships across seismic stations. Our approach processes multi-station waveform data and generates station-specific detection probabilities. Experiments show superior performance over a conventional GCN baseline in terms of true positive rate (TPR) and false positive rate (FPR), highlighting its potential for robust multi-station earthquake detection. The code repository for this study is available at https://github.com/SuchanunP/eq_detector.

A Survey of Graph Transformers: Architectures, Theories and Applications

Graph Transformers (GTs) have demonstrated a strong capability in modeling graph structures by addressing the intrinsic limitations of graph neural networks (GNNs), such as over-smoothing and over-squashing. Recent studies have proposed diverse architectures, enhanced explainability, and practical applications for Graph Transformers. In light of these rapid developments, we conduct a comprehensive review of Graph Transformers, covering aspects such as their architectures, theoretical foundations, and applications within this survey. We categorize the architecture of Graph Transformers according to their strategies for processing structural information, including graph tokenization, positional encoding, structure-aware attention and model ensemble. Furthermore, from the theoretical perspective, we examine the expressivity of Graph Transformers in various discussed architectures and contrast them with other advanced graph learning algorithms to discover the connections. Furthermore, we provide a summary of the practical applications where Graph Transformers have been utilized, such as molecule, protein, language, vision traffic, brain and material data. At the end of this survey, we will discuss the current challenges and prospective directions in Graph Transformers for potential future research.

Uncertainty Quantification With Noise Injection in Neural Networks: A Bayesian Perspective

Model uncertainty quantification involves measuring and evaluating the uncertainty linked to a model's predictions, helping assess their reliability and confidence. Noise injection is a technique used to enhance the robustness of neural networks by introducing randomness. In this paper, we establish a connection between noise injection and uncertainty quantification from a Bayesian standpoint. We theoretically demonstrate that injecting noise into the weights of a neural network is equivalent to Bayesian inference on a deep Gaussian process. Consequently, we introduce a Monte Carlo Noise Injection (MCNI) method, which involves injecting noise into the parameters during training and performing multiple forward propagations during inference to estimate the uncertainty of the prediction. Through simulation and experiments on regression and classification tasks, our method demonstrates superior performance compared to the baseline model.

Signal Processing over Time-Varying Graphs: A Systematic Review

As irregularly structured data representations, graphs have received a large amount of attention in recent years and have been widely applied to various real-world scenarios such as social, traffic, and energy settings. Compared to non-graph algorithms, numerous graph-based methodologies benefited from the strong power of graphs for representing high-dimensional and non-Euclidean data. In the field of Graph Signal Processing (GSP), analogies of classical signal processing concepts, such as shifting, convolution, filtering, and transformations are developed. However, many GSP techniques usually postulate the graph is static in both signal and typology. This assumption hinders the effectiveness of GSP methodologies as the assumption ignores the time-varying properties in numerous real-world systems. For example, in the traffic network, the signal on each node varies over time and contains underlying temporal correlation and patterns worthy of analysis. To tackle this challenge, more and more work are being done recently to investigate the processing of time-varying graph signals. They cope with time-varying challenges from three main directions: 1) graph time-spectral filtering, 2) multi-variate time-series forecasting, and 3) spatiotemporal graph data mining by neural networks, where non-negligible progress has been achieved. Despite the success of signal processing and learning over time-varying graphs, there is no survey to compare and conclude the current methodology for GSP and graph learning. To compensate for this, in this paper, we aim to review the development and recent progress on signal processing and learning over time-varying graphs, and compare their advantages and disadvantages from both the methodological and experimental side, to outline the challenges and potential research directions for future research.

LLM Online Spatial-temporal Signal Reconstruction Under Noise

This work introduces the LLM Online Spatial-temporal Reconstruction (LLM-OSR) framework, which integrates Graph Signal Processing (GSP) and Large Language Models (LLMs) for online spatial-temporal signal reconstruction. The LLM-OSR utilizes a GSP-based spatial-temporal signal handler to enhance graph signals and employs LLMs to predict missing values based on spatiotemporal patterns. The performance of LLM-OSR is evaluated on traffic and meteorological datasets under varying Gaussian noise levels. Experimental results demonstrate that utilizing GPT-4-o mini within the LLM-OSR is accurate and robust under Gaussian noise conditions. The limitations are discussed along with future research insights, emphasizing the potential of combining GSP techniques with LLMs for solving spatiotemporal prediction tasks.

LLM-based Online Prediction of Time-varying Graph Signals

In this paper, we propose a novel framework that leverages large language models (LLMs) for predicting missing values in time-varying graph signals by exploiting spatial and temporal smoothness. We leverage the power of LLM to achieve a message-passing scheme. For each missing node, its neighbors and previous estimates are fed into and processed by LLM to infer the missing observations. Tested on the task of the online prediction of wind-speed graph signals, our model outperforms online graph filtering algorithms in terms of accuracy, demonstrating the potential of LLMs in effectively addressing partially observed signals in graphs.

Time-varying Graph Signal Estimation via Dynamic Multi-hop Topologies

The assumption of using a static graph to represent multivariate time-varying signals oversimplifies the complexity of modeling their interactions over time. We propose a Dynamic Multi-hop model that captures dynamic interactions among time-varying node signals, while also accounting for time-varying edge signals, by extracting latent edges through topological diffusion and edge pruning. The resulting graphs are time-varying and sparse, capturing key dynamic node interactions and representing signal diffusion to both near and distant neighbors over time. The Dynamic Multi-hop Estimation algorithm is further proposed, accurately representing the interaction dynamics among node signals while enabling adaptive estimation of time-varying multivariate signals spatially and temporally. The Dynamic Multi-hop Estimation is evaluated under two real-world datasets of brain network and stock market for the online estimation of partially observed time-varying signals corrupted by noise.

Graph Signal Adaptive Message Passing

This paper proposes Graph Signal Adaptive Message Passing (GSAMP), a novel message passing method that simultaneously conducts online prediction, missing data imputation, and noise removal on time-varying graph signals. Unlike conventional Graph Signal Processing methods that apply the same filter to the entire graph, the spatiotemporal updates of GSAMP employ a distinct approach that utilizes localized computations at each node. This update is based on an adaptive solution obtained from an optimization problem designed to minimize the discrepancy between observed and estimated values. GSAMP effectively processes real-world, time-varying graph signals under Gaussian and impulsive noise conditions.