PAC-Bayes Information Bottleneck
Paper and Code
Oct 04, 2021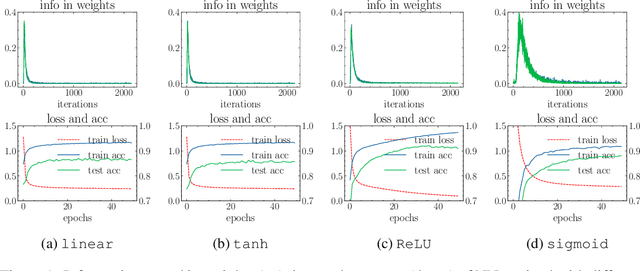

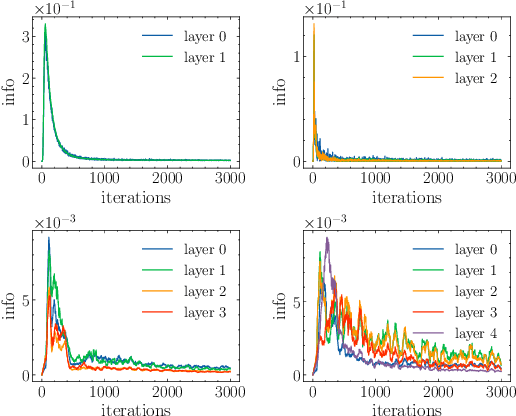
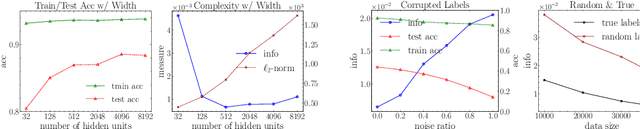
Information bottleneck (IB) depicts a trade-off between the accuracy and conciseness of encoded representations. IB has succeeded in explaining the objective and behavior of neural networks (NNs) as well as learning better representations. However, there are still critics of the universality of IB, e.g., phase transition usually fades away, representation compression is not causally related to generalization, and IB is trivial in deterministic cases. In this work, we build a new IB based on the trade-off between the accuracy and complexity of learned weights of NNs. We argue that this new IB represents a more solid connection to the objective of NNs since the information stored in weights (IIW) bounds their PAC-Bayes generalization capability, hence we name it as PAC-Bayes IB (PIB). On IIW, we can identify the phase transition phenomenon in general cases and solidify the causality between compression and generalization. We then derive a tractable solution of PIB and design a stochastic inference algorithm by Markov chain Monte Carlo sampling. We empirically verify our claims through extensive experiments. We also substantiate the superiority of the proposed algorithm on training NNs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge