Towards Scalable Modeling of Compressed Videos for Efficient Action Recognition

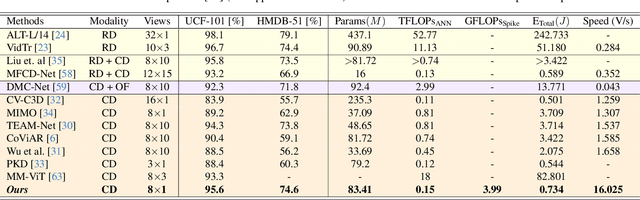
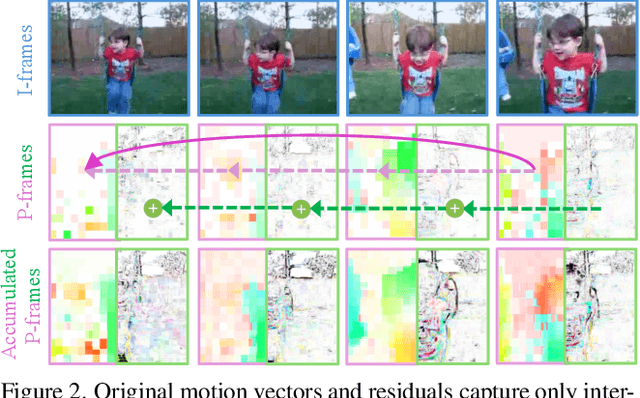
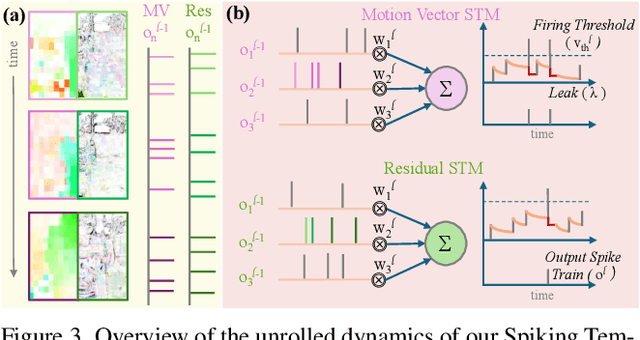
Training robust deep video representations has proven to be computationally challenging due to substantial decoding overheads, the enormous size of raw video streams, and their inherent high temporal redundancy. Different from existing schemes, operating exclusively in the compressed video domain and exploiting all freely available modalities, i.e., I-frames, and P-frames (motion vectors and residuals) offers a compute-efficient alternative. Existing methods approach this task as a naive multi-modality problem, ignoring the temporal correlation and implicit sparsity across P-frames for modeling stronger shared representations for videos of the same action, making training and generalization easier. By revisiting the high-level design of dominant video understanding backbones, we increase inference speed by a factor of $56$ while retaining similar performance. For this, we propose a hybrid end-to-end framework that factorizes learning across three key concepts to reduce inference cost by $330\times$ versus prior art: First, a specially designed dual-encoder scheme with efficient Spiking Temporal Modulators to minimize latency while retaining cross-domain feature aggregation. Second, a unified transformer model to capture inter-modal dependencies using global self-attention to enhance I-frame -- P-frame contextual interactions. Third, a Multi-Modal Mixer Block to model rich representations from the joint spatiotemporal token embeddings. Experiments show that our method results in a lightweight architecture achieving state-of-the-art video recognition performance on UCF-101, HMDB-51, K-400, K-600 and SS-v2 datasets with favorable costs ($0.73$J/V) and fast inference ($16$V/s). Our observations bring new insights into practical design choices for efficient next-generation spatiotemporal learners. Code is available.

Finding the Muses: Identifying Coresets through Loss Trajectories

Deep learning models achieve state-of-the-art performance across domains but face scalability challenges in real-time or resource-constrained scenarios. To address this, we propose Loss Trajectory Correlation (LTC), a novel metric for coreset selection that identifies critical training samples driving generalization. $LTC$ quantifies the alignment between training sample loss trajectories and validation set loss trajectories, enabling the construction of compact, representative subsets. Unlike traditional methods with computational and storage overheads that are infeasible to scale to large datasets, $LTC$ achieves superior efficiency as it can be computed as a byproduct of training. Our results on CIFAR-100 and ImageNet-1k show that $LTC$ consistently achieves accuracy on par with or surpassing state-of-the-art coreset selection methods, with any differences remaining under 1%. LTC also effectively transfers across various architectures, including ResNet, VGG, DenseNet, and Swin Transformer, with minimal performance degradation (<2%). Additionally, LTC offers insights into training dynamics, such as identifying aligned and conflicting sample behaviors, at a fraction of the computational cost of traditional methods. This framework paves the way for scalable coreset selection and efficient dataset optimization.

Plutus: Benchmarking Large Language Models in Low-Resource Greek Finance

Despite Greece's pivotal role in the global economy, large language models (LLMs) remain underexplored for Greek financial context due to the linguistic complexity of Greek and the scarcity of domain-specific datasets. Previous efforts in multilingual financial natural language processing (NLP) have exposed considerable performance disparities, yet no dedicated Greek financial benchmarks or Greek-specific financial LLMs have been developed until now. To bridge this gap, we introduce Plutus-ben, the first Greek Financial Evaluation Benchmark, and Plutus-8B, the pioneering Greek Financial LLM, fine-tuned with Greek domain-specific data. Plutus-ben addresses five core financial NLP tasks in Greek: numeric and textual named entity recognition, question answering, abstractive summarization, and topic classification, thereby facilitating systematic and reproducible LLM assessments. To underpin these tasks, we present three novel, high-quality Greek financial datasets, thoroughly annotated by expert native Greek speakers, augmented by two existing resources. Our comprehensive evaluation of 22 LLMs on Plutus-ben reveals that Greek financial NLP remains challenging due to linguistic complexity, domain-specific terminology, and financial reasoning gaps. These findings underscore the limitations of cross-lingual transfer, the necessity for financial expertise in Greek-trained models, and the challenges of adapting financial LLMs to Greek text. We release Plutus-ben, Plutus-8B, and all associated datasets publicly to promote reproducible research and advance Greek financial NLP, fostering broader multilingual inclusivity in finance.

Curvature Clues: Decoding Deep Learning Privacy with Input Loss Curvature

In this paper, we explore the properties of loss curvature with respect to input data in deep neural networks. Curvature of loss with respect to input (termed input loss curvature) is the trace of the Hessian of the loss with respect to the input. We investigate how input loss curvature varies between train and test sets, and its implications for train-test distinguishability. We develop a theoretical framework that derives an upper bound on the train-test distinguishability based on privacy and the size of the training set. This novel insight fuels the development of a new black box membership inference attack utilizing input loss curvature. We validate our theoretical findings through experiments in computer vision classification tasks, demonstrating that input loss curvature surpasses existing methods in membership inference effectiveness. Our analysis highlights how the performance of membership inference attack (MIA) methods varies with the size of the training set, showing that curvature-based MIA outperforms other methods on sufficiently large datasets. This condition is often met by real datasets, as demonstrated by our results on CIFAR10, CIFAR100, and ImageNet. These findings not only advance our understanding of deep neural network behavior but also improve the ability to test privacy-preserving techniques in machine learning.

Advancing Compressed Video Action Recognition through Progressive Knowledge Distillation

Compressed video action recognition classifies video samples by leveraging the different modalities in compressed videos, namely motion vectors, residuals, and intra-frames. For this purpose, three neural networks are deployed, each dedicated to processing one modality. Our observations indicate that the network processing intra-frames tend to converge to a flatter minimum than the network processing residuals, which in turn converges to a flatter minimum than the motion vector network. This hierarchy in convergence motivates our strategy for knowledge transfer among modalities to achieve flatter minima, which are generally associated with better generalization. With this insight, we propose Progressive Knowledge Distillation (PKD), a technique that incrementally transfers knowledge across the modalities. This method involves attaching early exits (Internal Classifiers - ICs) to the three networks. PKD distills knowledge starting from the motion vector network, followed by the residual, and finally, the intra-frame network, sequentially improving IC accuracy. Further, we propose the Weighted Inference with Scaled Ensemble (WISE), which combines outputs from the ICs using learned weights, boosting accuracy during inference. Our experiments demonstrate the effectiveness of training the ICs with PKD compared to standard cross-entropy-based training, showing IC accuracy improvements of up to 5.87% and 11.42% on the UCF-101 and HMDB-51 datasets, respectively. Additionally, WISE improves accuracy by up to 4.28% and 9.30% on UCF-101 and HMDB-51, respectively.

Unveiling Privacy, Memorization, and Input Curvature Links

Deep Neural Nets (DNNs) have become a pervasive tool for solving many emerging problems. However, they tend to overfit to and memorize the training set. Memorization is of keen interest since it is closely related to several concepts such as generalization, noisy learning, and privacy. To study memorization, Feldman (2019) proposed a formal score, however its computational requirements limit its practical use. Recent research has shown empirical evidence linking input loss curvature (measured by the trace of the loss Hessian w.r.t inputs) and memorization. It was shown to be ~3 orders of magnitude more efficient than calculating the memorization score. However, there is a lack of theoretical understanding linking memorization with input loss curvature. In this paper, we not only investigate this connection but also extend our analysis to establish theoretical links between differential privacy, memorization, and input loss curvature. First, we derive an upper bound on memorization characterized by both differential privacy and input loss curvature. Second, we present a novel insight showing that input loss curvature is upper-bounded by the differential privacy parameter. Our theoretical findings are further empirically validated using deep models on CIFAR and ImageNet datasets, showing a strong correlation between our theoretical predictions and results observed in practice.

Synthetic Dataset Generation for Privacy-Preserving Machine Learning

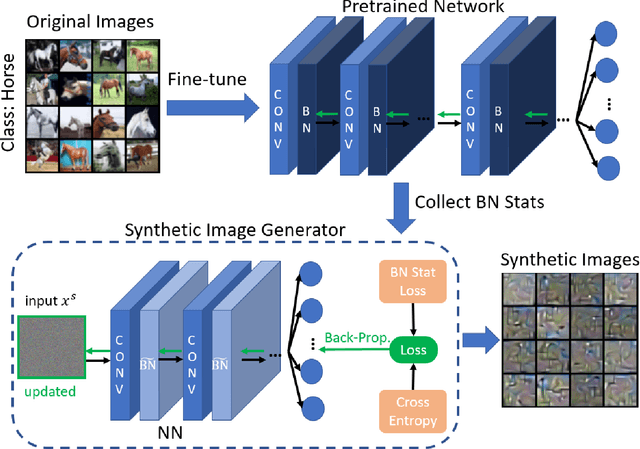
Machine Learning (ML) has achieved enormous success in solving a variety of problems in computer vision, speech recognition, object detection, to name a few. The principal reason for this success is the availability of huge datasets for training deep neural networks (DNNs). However, datasets cannot be publicly released if they contain sensitive information such as medical records, and data privacy becomes a major concern. Encryption methods could be a possible solution, however their deployment on ML applications seriously impacts classification accuracy and results in substantial computational overhead. Alternatively, obfuscation techniques could be used, but maintaining a good trade-off between visual privacy and accuracy is challenging. In this paper, we propose a method to generate secure synthetic datasets from the original private datasets. Given a network with Batch Normalization (BN) layers pretrained on the original dataset, we first record the class-wise BN layer statistics. Next, we generate the synthetic dataset by optimizing random noise such that the synthetic data match the layer-wise statistical distribution of original images. We evaluate our method on image classification datasets (CIFAR10, ImageNet) and show that synthetic data can be used in place of the original CIFAR10/ImageNet data for training networks from scratch, producing comparable classification performance. Further, to analyze visual privacy provided by our method, we use Image Quality Metrics and show high degree of visual dissimilarity between the original and synthetic images. Moreover, we show that our proposed method preserves data-privacy under various privacy-leakage attacks including Gradient Matching Attack, Model Memorization Attack, and GAN-based Attack.

Evaluating the Stability of Recurrent Neural Models during Training with Eigenvalue Spectra Analysis

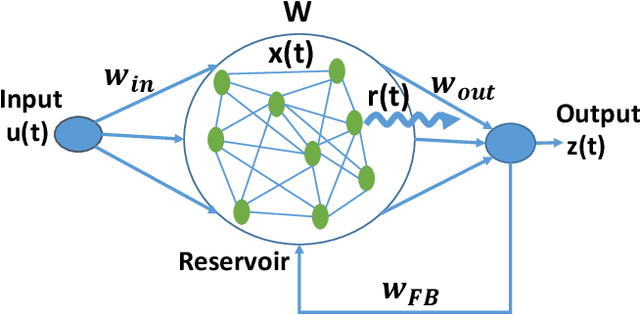
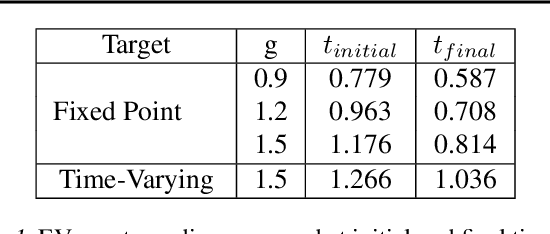
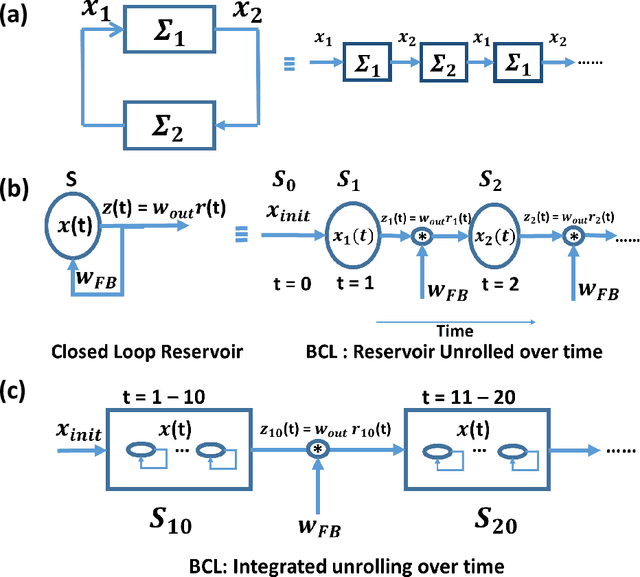
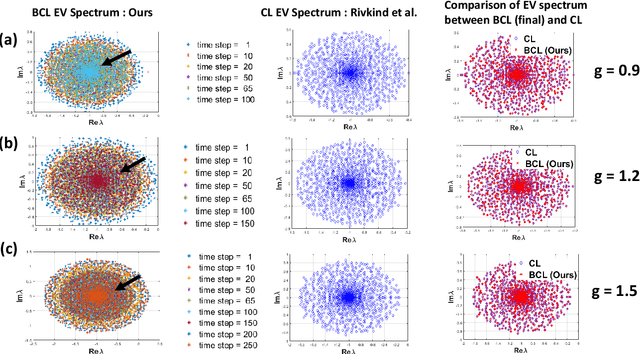
We analyze the stability of recurrent networks, specifically, reservoir computing models during training by evaluating the eigenvalue spectra of the reservoir dynamics. To circumvent the instability arising in examining a closed loop reservoir system with feedback, we propose to break the closed loop system. Essentially, we unroll the reservoir dynamics over time while incorporating the feedback effects that preserve the overall temporal integrity of the system. We evaluate our methodology for fixed point and time varying targets with least squares regression and FORCE training, respectively. Our analysis establishes eigenvalue spectra (which is, shrinking of spectral circle as training progresses) as a valid and effective metric to gauge the convergence of training as well as the convergence of the chaotic activity of the reservoir toward stable states.