Curvature Clues: Decoding Deep Learning Privacy with Input Loss Curvature

In this paper, we explore the properties of loss curvature with respect to input data in deep neural networks. Curvature of loss with respect to input (termed input loss curvature) is the trace of the Hessian of the loss with respect to the input. We investigate how input loss curvature varies between train and test sets, and its implications for train-test distinguishability. We develop a theoretical framework that derives an upper bound on the train-test distinguishability based on privacy and the size of the training set. This novel insight fuels the development of a new black box membership inference attack utilizing input loss curvature. We validate our theoretical findings through experiments in computer vision classification tasks, demonstrating that input loss curvature surpasses existing methods in membership inference effectiveness. Our analysis highlights how the performance of membership inference attack (MIA) methods varies with the size of the training set, showing that curvature-based MIA outperforms other methods on sufficiently large datasets. This condition is often met by real datasets, as demonstrated by our results on CIFAR10, CIFAR100, and ImageNet. These findings not only advance our understanding of deep neural network behavior but also improve the ability to test privacy-preserving techniques in machine learning.

Advancing Compressed Video Action Recognition through Progressive Knowledge Distillation

Compressed video action recognition classifies video samples by leveraging the different modalities in compressed videos, namely motion vectors, residuals, and intra-frames. For this purpose, three neural networks are deployed, each dedicated to processing one modality. Our observations indicate that the network processing intra-frames tend to converge to a flatter minimum than the network processing residuals, which in turn converges to a flatter minimum than the motion vector network. This hierarchy in convergence motivates our strategy for knowledge transfer among modalities to achieve flatter minima, which are generally associated with better generalization. With this insight, we propose Progressive Knowledge Distillation (PKD), a technique that incrementally transfers knowledge across the modalities. This method involves attaching early exits (Internal Classifiers - ICs) to the three networks. PKD distills knowledge starting from the motion vector network, followed by the residual, and finally, the intra-frame network, sequentially improving IC accuracy. Further, we propose the Weighted Inference with Scaled Ensemble (WISE), which combines outputs from the ICs using learned weights, boosting accuracy during inference. Our experiments demonstrate the effectiveness of training the ICs with PKD compared to standard cross-entropy-based training, showing IC accuracy improvements of up to 5.87% and 11.42% on the UCF-101 and HMDB-51 datasets, respectively. Additionally, WISE improves accuracy by up to 4.28% and 9.30% on UCF-101 and HMDB-51, respectively.

Verifix: Post-Training Correction to Improve Label Noise Robustness with Verified Samples

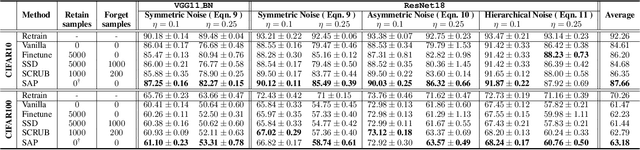
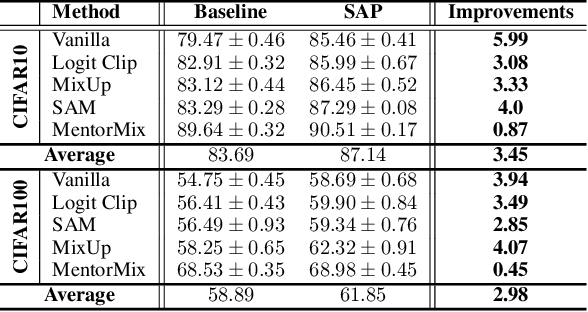
Label corruption, where training samples have incorrect labels, can significantly degrade the performance of machine learning models. This corruption often arises from non-expert labeling or adversarial attacks. Acquiring large, perfectly labeled datasets is costly, and retraining large models from scratch when a clean dataset becomes available is computationally expensive. To address this challenge, we propose Post-Training Correction, a new paradigm that adjusts model parameters after initial training to mitigate label noise, eliminating the need for retraining. We introduce Verifix, a novel Singular Value Decomposition (SVD) based algorithm that leverages a small, verified dataset to correct the model weights using a single update. Verifix uses SVD to estimate a Clean Activation Space and then projects the model's weights onto this space to suppress activations corresponding to corrupted data. We demonstrate Verifix's effectiveness on both synthetic and real-world label noise. Experiments on the CIFAR dataset with 25% synthetic corruption show 7.36% generalization improvements on average. Additionally, we observe generalization improvements of up to 2.63% on naturally corrupted datasets like WebVision1.0 and Clothing1M.

Unveiling Privacy, Memorization, and Input Curvature Links

Deep Neural Nets (DNNs) have become a pervasive tool for solving many emerging problems. However, they tend to overfit to and memorize the training set. Memorization is of keen interest since it is closely related to several concepts such as generalization, noisy learning, and privacy. To study memorization, Feldman (2019) proposed a formal score, however its computational requirements limit its practical use. Recent research has shown empirical evidence linking input loss curvature (measured by the trace of the loss Hessian w.r.t inputs) and memorization. It was shown to be ~3 orders of magnitude more efficient than calculating the memorization score. However, there is a lack of theoretical understanding linking memorization with input loss curvature. In this paper, we not only investigate this connection but also extend our analysis to establish theoretical links between differential privacy, memorization, and input loss curvature. First, we derive an upper bound on memorization characterized by both differential privacy and input loss curvature. Second, we present a novel insight showing that input loss curvature is upper-bounded by the differential privacy parameter. Our theoretical findings are further empirically validated using deep models on CIFAR and ImageNet datasets, showing a strong correlation between our theoretical predictions and results observed in practice.

Homogenizing Non-IID datasets via In-Distribution Knowledge Distillation for Decentralized Learning

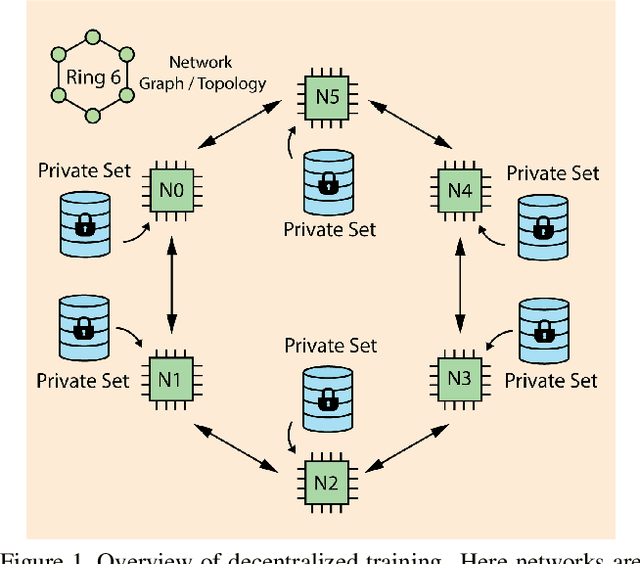
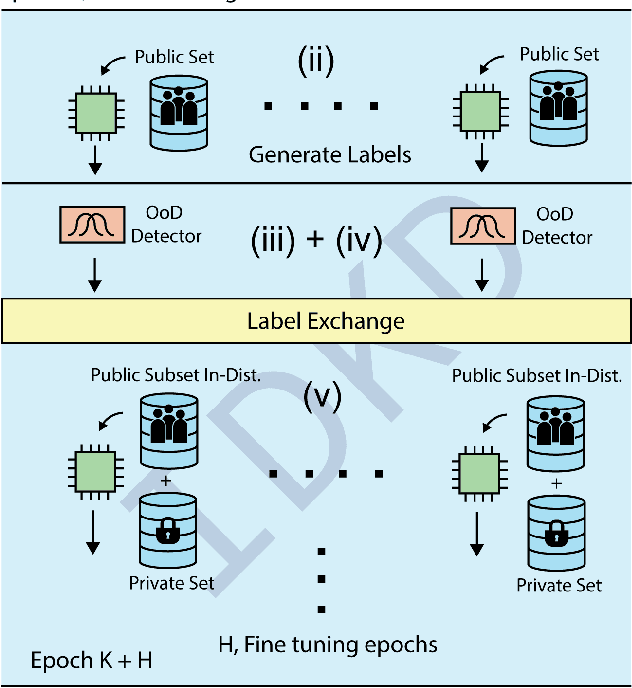
Decentralized learning enables serverless training of deep neural networks (DNNs) in a distributed manner on multiple nodes. This allows for the use of large datasets, as well as the ability to train with a wide variety of data sources. However, one of the key challenges with decentralized learning is heterogeneity in the data distribution across the nodes. In this paper, we propose In-Distribution Knowledge Distillation (IDKD) to address the challenge of heterogeneous data distribution. The goal of IDKD is to homogenize the data distribution across the nodes. While such data homogenization can be achieved by exchanging data among the nodes sacrificing privacy, IDKD achieves the same objective using a common public dataset across nodes without breaking the privacy constraint. This public dataset is different from the training dataset and is used to distill the knowledge from each node and communicate it to its neighbors through the generated labels. With traditional knowledge distillation, the generalization of the distilled model is reduced because all the public dataset samples are used irrespective of their similarity to the local dataset. Thus, we introduce an Out-of-Distribution (OoD) detector at each node to label a subset of the public dataset that maps close to the local training data distribution. Finally, only labels corresponding to these subsets are exchanged among the nodes and with appropriate label averaging each node is finetuned on these data subsets along with its local data. Our experiments on multiple image classification datasets and graph topologies show that the proposed IDKD scheme is more effective than traditional knowledge distillation and achieves state-of-the-art generalization performance on heterogeneously distributed data with minimal communication overhead.

Norm-Scaling for Out-of-Distribution Detection

Out-of-Distribution (OoD) inputs are examples that do not belong to the true underlying distribution of the dataset. Research has shown that deep neural nets make confident mispredictions on OoD inputs. Therefore, it is critical to identify OoD inputs for safe and reliable deployment of deep neural nets. Often a threshold is applied on a similarity score to detect OoD inputs. One such similarity is angular similarity which is the dot product of latent representation with the mean class representation. Angular similarity encodes uncertainty, for example, if the angular similarity is less, it is less certain that the input belongs to that class. However, we observe that, different classes have different distributions of angular similarity. Therefore, applying a single threshold for all classes is not ideal since the same similarity score represents different uncertainties for different classes. In this paper, we propose norm-scaling which normalizes the logits separately for each class. This ensures that a single value consistently represents similar uncertainty for various classes. We show that norm-scaling, when used with maximum softmax probability detector, achieves 9.78% improvement in AUROC, 5.99% improvement in AUPR and 33.19% reduction in FPR95 metrics over previous state-of-the-art methods.

Exploring Vicinal Risk Minimization for Lightweight Out-of-Distribution Detection

Deep neural networks have found widespread adoption in solving complex tasks ranging from image recognition to natural language processing. However, these networks make confident mispredictions when presented with data that does not belong to the training distribution, i.e. out-of-distribution (OoD) samples. In this paper we explore whether the property of Vicinal Risk Minimization (VRM) to smoothly interpolate between different class boundaries helps to train better OoD detectors. We apply VRM to existing OoD detection techniques and show their improved performance. We observe that existing OoD detectors have significant memory and compute overhead, hence we leverage VRM to develop an OoD detector with minimal overheard. Our detection method introduces an auxiliary class for classifying OoD samples. We utilize mixup in two ways to implement Vicinal Risk Minimization. First, we perform mixup within the same class and second, we perform mixup with Gaussian noise when training the auxiliary class. Our method achieves near competitive performance with significantly less compute and memory overhead when compared to existing OoD detection techniques. This facilitates the deployment of OoD detection on edge devices and expands our understanding of Vicinal Risk Minimization for use in training OoD detectors.

TREND: Transferability based Robust ENsemble Design

Deep Learning models hold state-of-the-art performance in many fields, but their vulnerability to adversarial examples poses a threat to their ubiquitous deployment in practical settings. Additionally, adversarial inputs generated on one classifier have been shown to transfer to other classifiers trained on similar data, which makes the attacks possible even if the model parameters are not revealed to the adversary. This property of transferability has not yet been systematically studied, leading to a gap in our understanding of robustness of neural networks to adversarial inputs. In this work, we study the effect of network architecture, initialization, input, weight and activation quantization on transferability. Our experiments reveal that transferability is significantly hampered by input quantization and architectural mismatch between source and target, is unaffected by initialization and is architecture-dependent for both weight and activation quantization. To quantify transferability, we propose a simple metric, which is a function of the attack strength. We demonstrate the utility of the proposed metric in designing a methodology to build ensembles with improved adversarial robustness. Finally, we show that an ensemble consisting of carefully chosen input quantized networks achieves better adversarial robustness than would otherwise be possible with a single network.