Evaluating the Stability of Recurrent Neural Models during Training with Eigenvalue Spectra Analysis
Paper and Code
May 08, 2019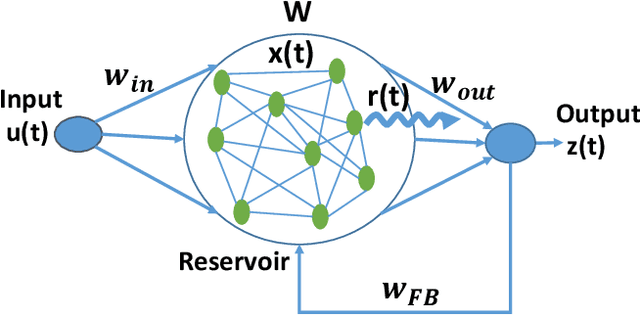
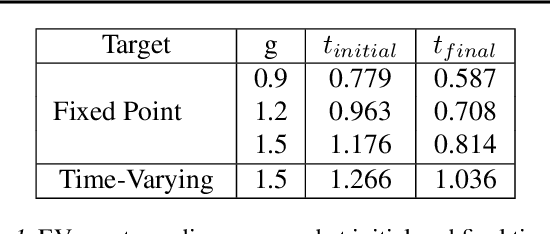
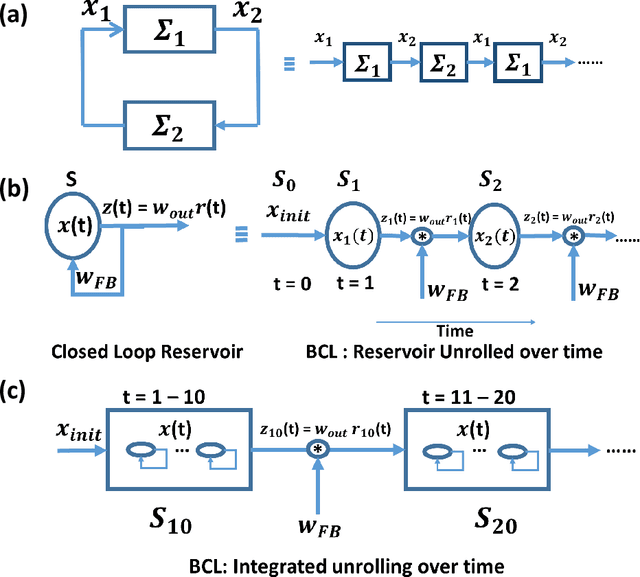
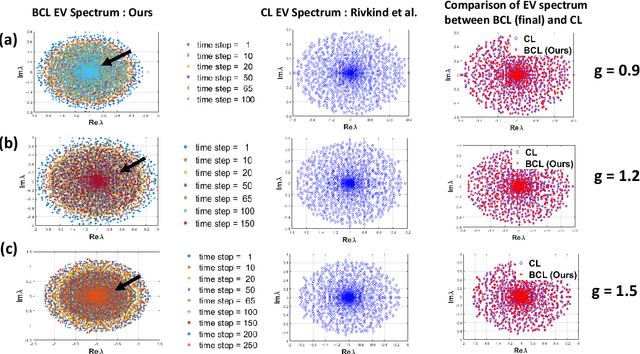
We analyze the stability of recurrent networks, specifically, reservoir computing models during training by evaluating the eigenvalue spectra of the reservoir dynamics. To circumvent the instability arising in examining a closed loop reservoir system with feedback, we propose to break the closed loop system. Essentially, we unroll the reservoir dynamics over time while incorporating the feedback effects that preserve the overall temporal integrity of the system. We evaluate our methodology for fixed point and time varying targets with least squares regression and FORCE training, respectively. Our analysis establishes eigenvalue spectra (which is, shrinking of spectral circle as training progresses) as a valid and effective metric to gauge the convergence of training as well as the convergence of the chaotic activity of the reservoir toward stable states.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge