Machine learning for modelling unstructured grid data in computational physics: a review

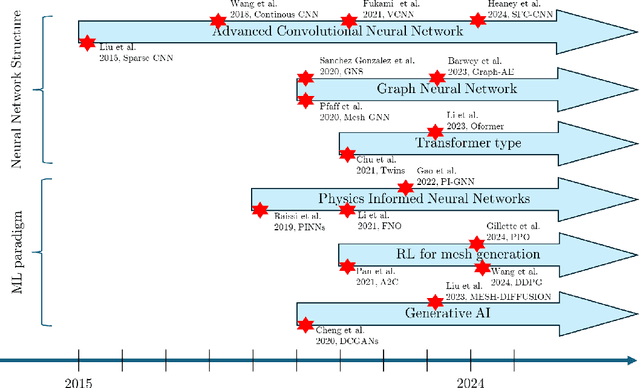
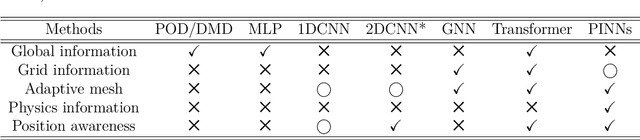
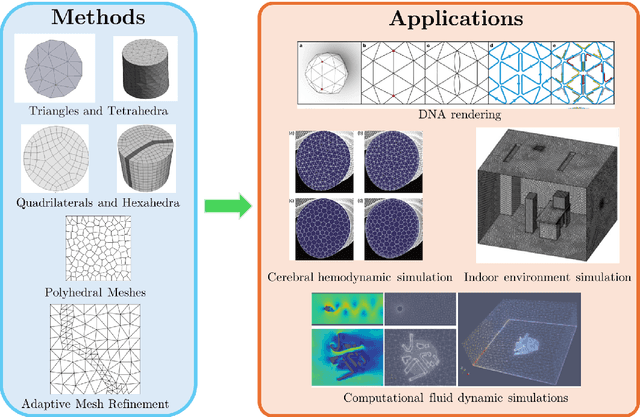
Unstructured grid data are essential for modelling complex geometries and dynamics in computational physics. Yet, their inherent irregularity presents significant challenges for conventional machine learning (ML) techniques. This paper provides a comprehensive review of advanced ML methodologies designed to handle unstructured grid data in high-dimensional dynamical systems. Key approaches discussed include graph neural networks, transformer models with spatial attention mechanisms, interpolation-integrated ML methods, and meshless techniques such as physics-informed neural networks. These methodologies have proven effective across diverse fields, including fluid dynamics and environmental simulations. This review is intended as a guidebook for computational scientists seeking to apply ML approaches to unstructured grid data in their domains, as well as for ML researchers looking to address challenges in computational physics. It places special focus on how ML methods can overcome the inherent limitations of traditional numerical techniques and, conversely, how insights from computational physics can inform ML development. To support benchmarking, this review also provides a summary of open-access datasets of unstructured grid data in computational physics. Finally, emerging directions such as generative models with unstructured data, reinforcement learning for mesh generation, and hybrid physics-data-driven paradigms are discussed to inspire future advancements in this evolving field.

Parametric Taylor series based latent dynamics identification neural networks

Numerical solving parameterised partial differential equations (P-PDEs) is highly practical yet computationally expensive, driving the development of reduced-order models (ROMs). Recently, methods that combine latent space identification techniques with deep learning algorithms (e.g., autoencoders) have shown great potential in describing the dynamical system in the lower dimensional latent space, for example, LaSDI, gLaSDI and GPLaSDI. In this paper, a new parametric latent identification of nonlinear dynamics neural networks, P-TLDINets, is introduced, which relies on a novel neural network structure based on Taylor series expansion and ResNets to learn the ODEs that govern the reduced space dynamics. During the training process, Taylor series-based Latent Dynamic Neural Networks (TLDNets) and identified equations are trained simultaneously to generate a smoother latent space. In order to facilitate the parameterised study, a $k$-nearest neighbours (KNN) method based on an inverse distance weighting (IDW) interpolation scheme is introduced to predict the identified ODE coefficients using local information. Compared to other latent dynamics identification methods based on autoencoders, P-TLDINets remain the interpretability of the model. Additionally, it circumvents the building of explicit autoencoders, avoids dependency on specific grids, and features a more lightweight structure, which is easy to train with high generalisation capability and accuracy. Also, it is capable of using different scales of meshes. P-TLDINets improve training speeds nearly hundred times compared to GPLaSDI and gLaSDI, maintaining an $L_2$ error below $2\%$ compared to high-fidelity models.

Machine learning with data assimilation and uncertainty quantification for dynamical systems: a review

Data Assimilation (DA) and Uncertainty quantification (UQ) are extensively used in analysing and reducing error propagation in high-dimensional spatial-temporal dynamics. Typical applications span from computational fluid dynamics (CFD) to geoscience and climate systems. Recently, much effort has been given in combining DA, UQ and machine learning (ML) techniques. These research efforts seek to address some critical challenges in high-dimensional dynamical systems, including but not limited to dynamical system identification, reduced order surrogate modelling, error covariance specification and model error correction. A large number of developed techniques and methodologies exhibit a broad applicability across numerous domains, resulting in the necessity for a comprehensive guide. This paper provides the first overview of the state-of-the-art researches in this interdisciplinary field, covering a wide range of applications. This review aims at ML scientists who attempt to apply DA and UQ techniques to improve the accuracy and the interpretability of their models, but also at DA and UQ experts who intend to integrate cutting-edge ML approaches to their systems. Therefore, this article has a special focus on how ML methods can overcome the existing limits of DA and UQ, and vice versa. Some exciting perspectives of this rapidly developing research field are also discussed.

Egret Swarm Optimization Algorithm: An Evolutionary Computation Approach for Model Free Optimization

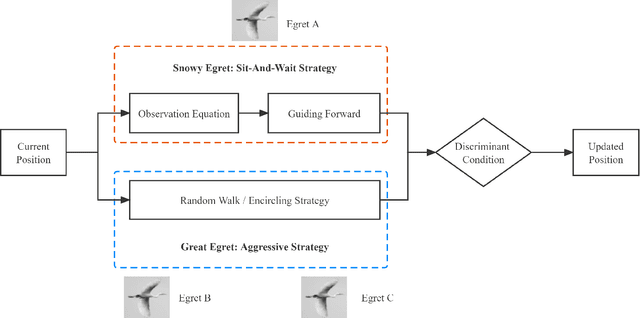
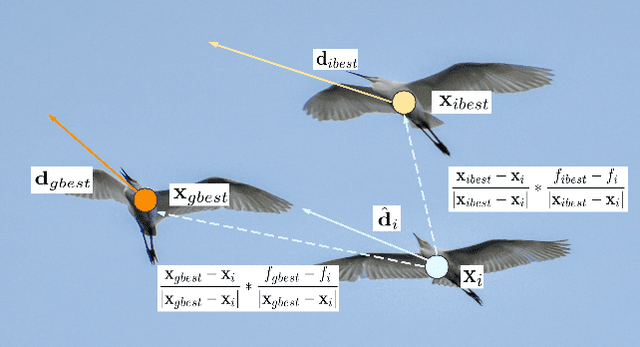
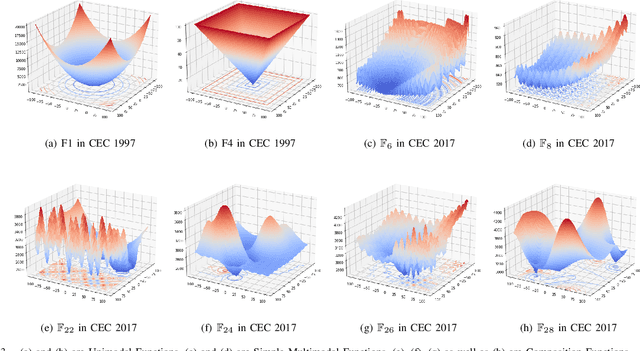
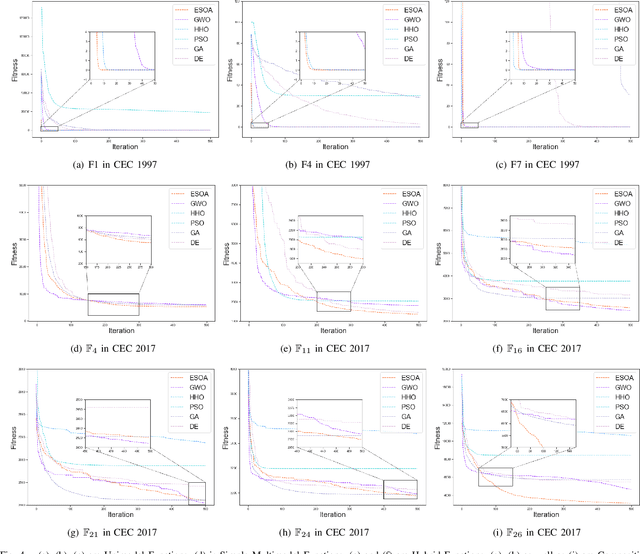
A novel meta-heuristic algorithm, Egret Swarm Optimization Algorithm (ESOA), is proposed in this paper, which is inspired by two egret species' (Great Egret and Snowy Egret) hunting behavior. ESOA consists of three primary components: Sit-And-Wait Strategy, Aggressive Strategy as well as Discriminant Conditions. The performance of ESOA on 36 benchmark functions as well as 2 engineering problems are compared with Particle Swarm Optimization (PSO), Genetic Algorithm (GA), Differential Evolution (DE), Grey Wolf Optimizer (GWO), and Harris Hawks Optimization (HHO). The result proves the superior effectiveness and robustness of ESOA. The source code used in this work can be retrieved from https://github.com/Knightsll/Egret_Swarm_Optimization_Algorithm; https://ww2.mathworks.cn/matlabcentral/fileexchange/115595-egret-swarm-optimization-algorithm-esoa.