IterNorm: Fast Iterative Normalization

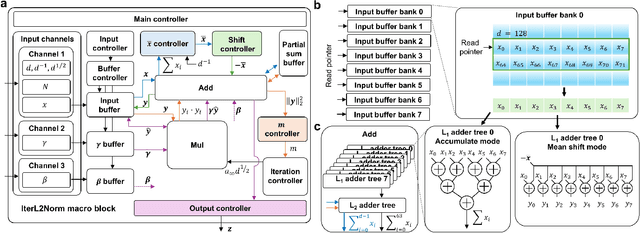
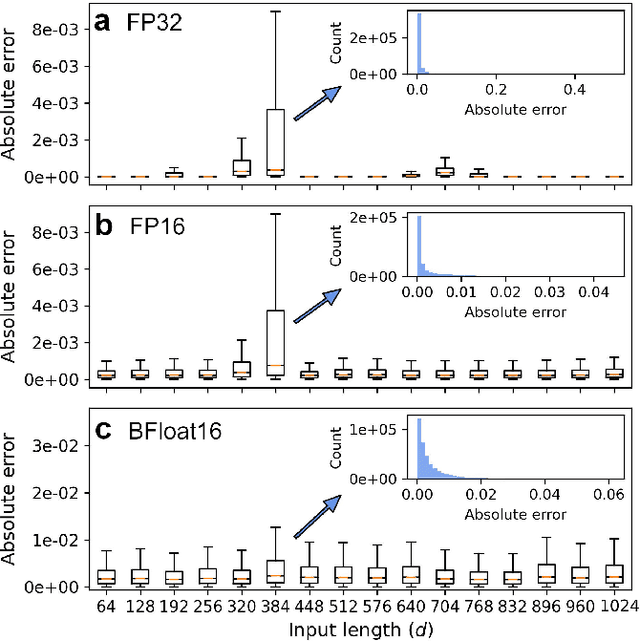
Transformer-based large language models are a memory-bound model whose operation is based on a large amount of data that are marginally reused. Thus, the data movement between a host and accelerator likely dictates the total wall-clock time. Layer normalization is one of the key workloads in the transformer model, following each of multi-head attention and feed-forward network blocks. To reduce data movement, layer normalization needs to be performed on the same chip as the matrix-matrix multiplication engine. To this end, we introduce an iterative L2-normalization method for 1D input (IterNorm), ensuring fast convergence to the steady-state solution within five iteration steps and high precision, outperforming the fast inverse square root algorithm in six out of nine cases for FP32 and five out of nine for BFloat16 across the embedding lengths used in the OPT models. Implemented in 32/28nm CMOS, the IterNorm macro normalizes $d$-dimensional vectors, where $64 \leq d \leq 1024$, with a latency of 112-227 cycles at 100MHz/1.05V.

CBP: Backpropagation with constraint on weight precision using a pseudo-Lagrange multiplier method

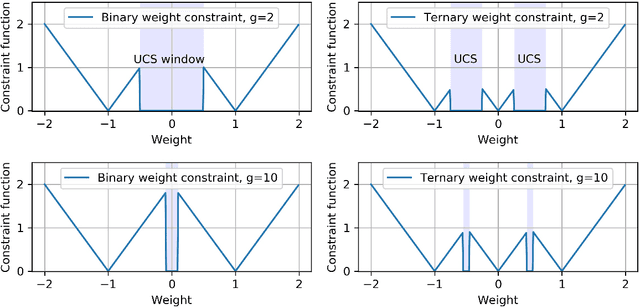
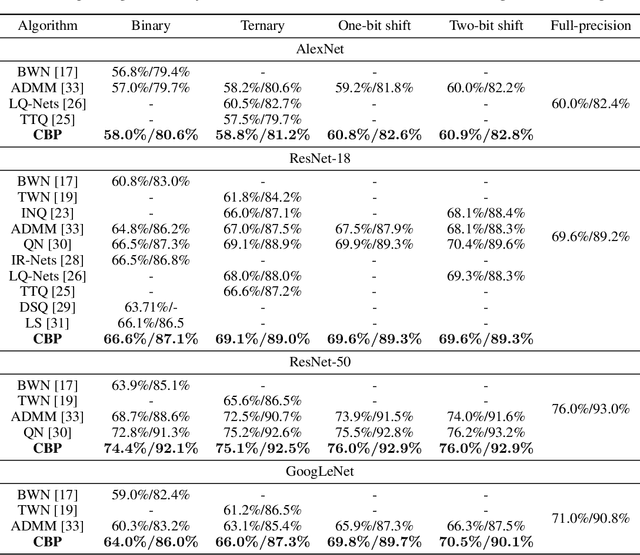
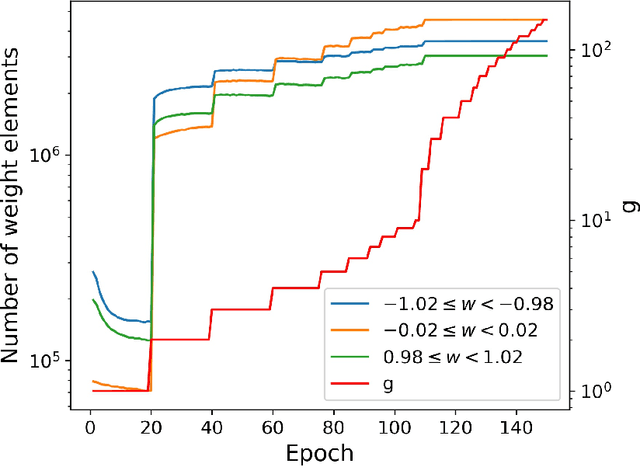
Backward propagation of errors (backpropagation) is a method to minimize objective functions (e.g., loss functions) of deep neural networks by identifying optimal sets of weights and biases. Imposing constraints on weight precision is often required to alleviate prohibitive workloads on hardware. Despite the remarkable success of backpropagation, the algorithm itself is not capable of considering such constraints unless additional algorithms are applied simultaneously. To address this issue, we propose the constrained backpropagation (CBP) algorithm based on a pseudo-Lagrange multiplier method to obtain the optimal set of weights that satisfy a given set of constraints. The defining characteristic of the proposed CBP algorithm is the utilization of a Lagrangian function (loss function plus constraint function) as its objective function. We considered various types of constraints--binary, ternary, one-bit shift, and two-bit shift weight constraints. As a post-training method, CBP applied to AlexNet, ResNet-18, ResNet-50, and GoogLeNet on ImageNet, which were pre-trained using the conventional backpropagation. For all cases, the proposed algorithm outperforms the state-of-the-art methods on ImageNet, e.g., 66.6%, 74.4%, and 64.0% top-1 accuracy for ResNet-18, ResNet-50, and GoogLeNet with binary weights, respectively. This highlights CBP as a learning algorithm to address diverse constraints with the minimal performance loss by employing appropriate constraint functions.

Training Spiking Neural Networks Using Lessons From Deep Learning

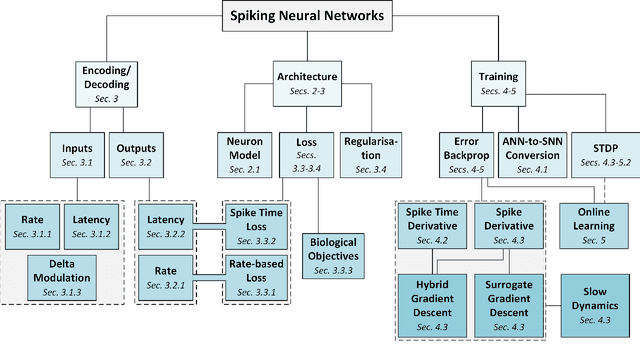
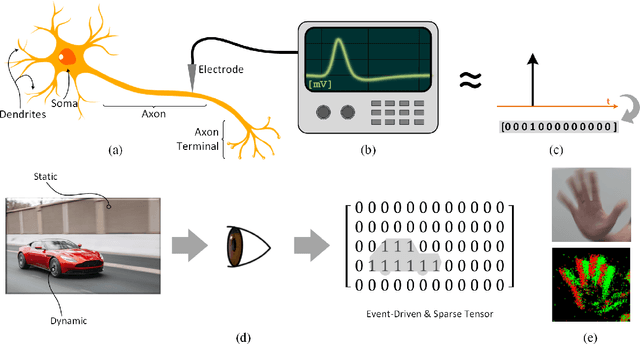
The brain is the perfect place to look for inspiration to develop more efficient neural networks. The inner workings of our synapses and neurons provide a glimpse at what the future of deep learning might look like. This paper serves as a tutorial and perspective showing how to apply the lessons learnt from several decades of research in deep learning, gradient descent, backpropagation and neuroscience to biologically plausible spiking neural neural networks. We also explore the delicate interplay between encoding data as spikes and the learning process; the challenges and solutions of applying gradient-based learning to spiking neural networks; the subtle link between temporal backpropagation and spike timing dependent plasticity, and how deep learning might move towards biologically plausible online learning. Some ideas are well accepted and commonly used amongst the neuromorphic engineering community, while others are presented or justified for the first time here. A series of companion interactive tutorials complementary to this paper using our Python package, snnTorch, are also made available: https://snntorch.readthedocs.io/en/latest/tutorials/index.html

Simplified calcium signaling cascade for synaptic plasticity

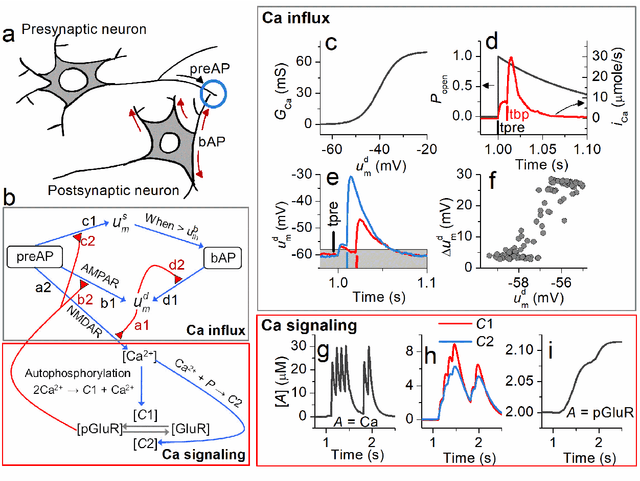
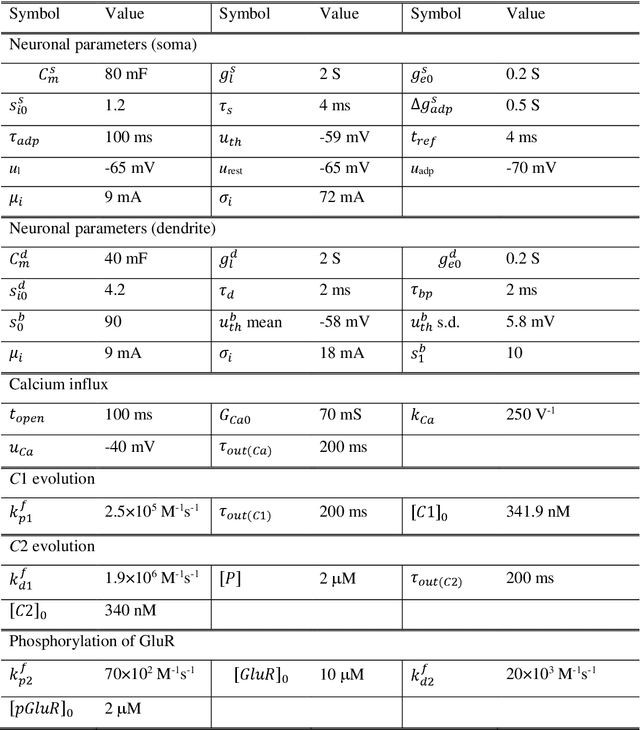
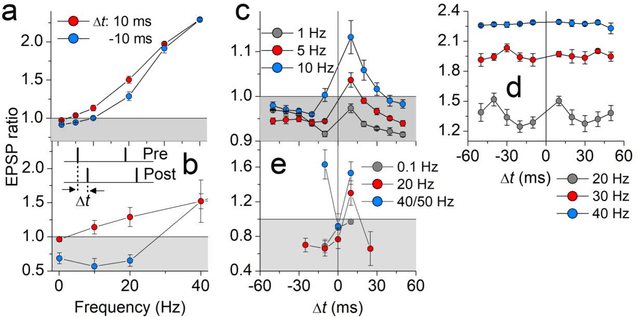
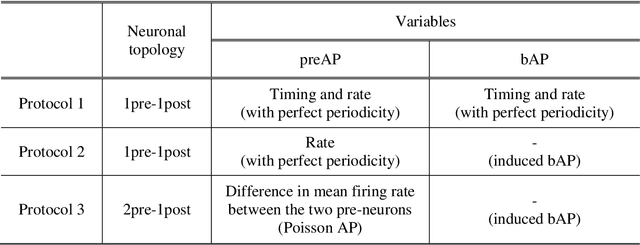
We propose a model for synaptic plasticity based on a calcium signaling cascade. The model simplifies the full signaling pathways from a calcium influx to the phosphorylation (potentiation) and dephosphorylation (depression) of glutamate receptors that are gated by fictive C1 and C2 catalysts, respectively. This model is based on tangible chemical reactions, including fictive catalysts, for long-term plasticity rather than the conceptual theories commonplace in various models, such as preset thresholds of calcium concentration. Our simplified model successfully reproduced the experimental synaptic plasticity induced by different protocols such as (i) a synchronous pairing protocol and (ii) correlated presynaptic and postsynaptic action potentials (APs). Further, the ocular dominance plasticity (or the experimental verification of the celebrated Bienenstock--Cooper--Munro theory) was reproduced by two model synapses that compete by means of back-propagating APs (bAPs). The key to this competition is synapse-specific bAPs with reference to bAP-boosting on the physiological grounds.

Markov chain Hebbian learning algorithm with ternary synaptic units

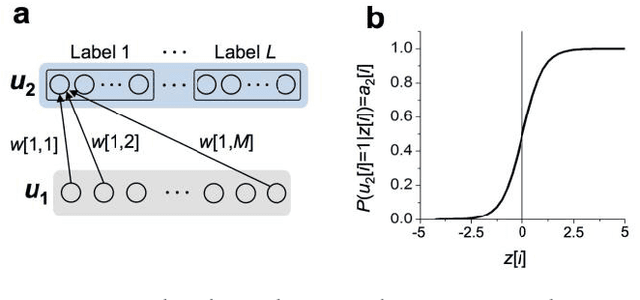
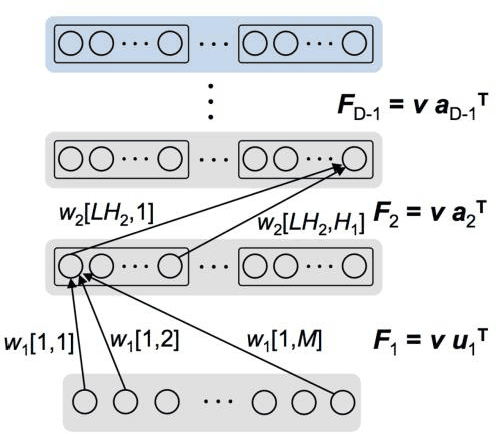
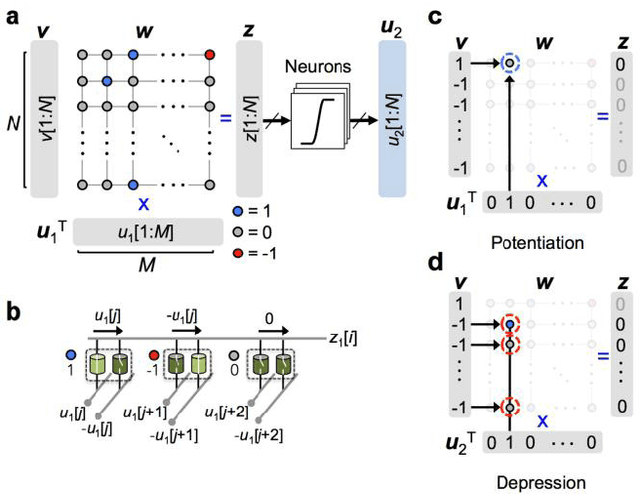
In spite of remarkable progress in machine learning techniques, the state-of-the-art machine learning algorithms often keep machines from real-time learning (online learning) due in part to computational complexity in parameter optimization. As an alternative, a learning algorithm to train a memory in real time is proposed, which is named as the Markov chain Hebbian learning algorithm. The algorithm pursues efficient memory use during training in that (i) the weight matrix has ternary elements (-1, 0, 1) and (ii) each update follows a Markov chain--the upcoming update does not need past weight memory. The algorithm was verified by two proof-of-concept tasks (handwritten digit recognition and multiplication table memorization) in which numbers were taken as symbols. Particularly, the latter bases multiplication arithmetic on memory, which may be analogous to humans' mental arithmetic. The memory-based multiplication arithmetic feasibly offers the basis of factorization, supporting novel insight into the arithmetic.