CBP: Backpropagation with constraint on weight precision using a pseudo-Lagrange multiplier method
Paper and Code
Oct 06, 2021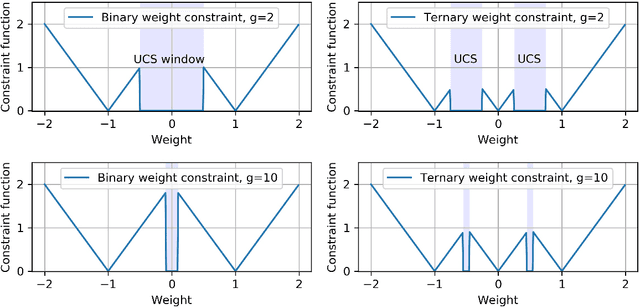
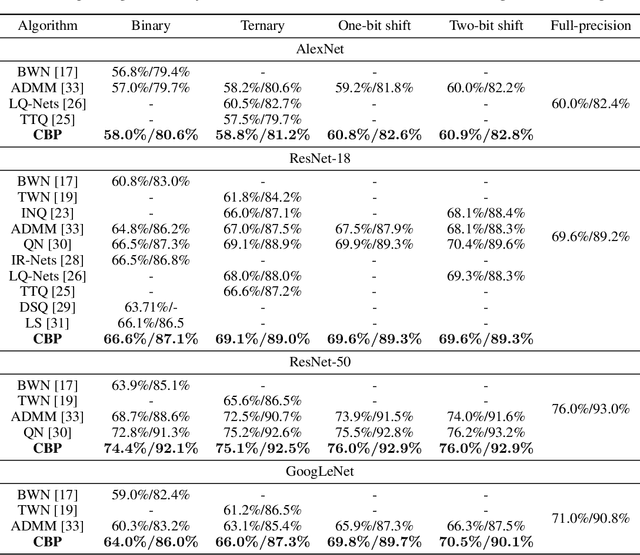
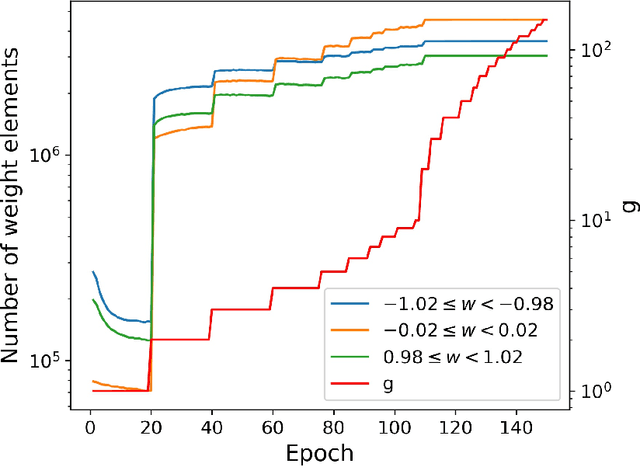

Backward propagation of errors (backpropagation) is a method to minimize objective functions (e.g., loss functions) of deep neural networks by identifying optimal sets of weights and biases. Imposing constraints on weight precision is often required to alleviate prohibitive workloads on hardware. Despite the remarkable success of backpropagation, the algorithm itself is not capable of considering such constraints unless additional algorithms are applied simultaneously. To address this issue, we propose the constrained backpropagation (CBP) algorithm based on a pseudo-Lagrange multiplier method to obtain the optimal set of weights that satisfy a given set of constraints. The defining characteristic of the proposed CBP algorithm is the utilization of a Lagrangian function (loss function plus constraint function) as its objective function. We considered various types of constraints--binary, ternary, one-bit shift, and two-bit shift weight constraints. As a post-training method, CBP applied to AlexNet, ResNet-18, ResNet-50, and GoogLeNet on ImageNet, which were pre-trained using the conventional backpropagation. For all cases, the proposed algorithm outperforms the state-of-the-art methods on ImageNet, e.g., 66.6%, 74.4%, and 64.0% top-1 accuracy for ResNet-18, ResNet-50, and GoogLeNet with binary weights, respectively. This highlights CBP as a learning algorithm to address diverse constraints with the minimal performance loss by employing appropriate constraint functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge