Gradient Scaling on Deep Spiking Neural Networks with Spike-Dependent Local Information

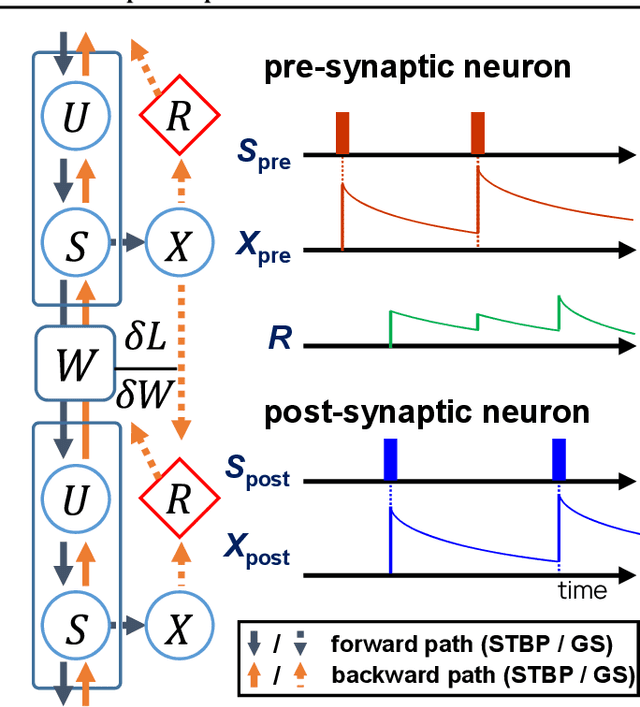
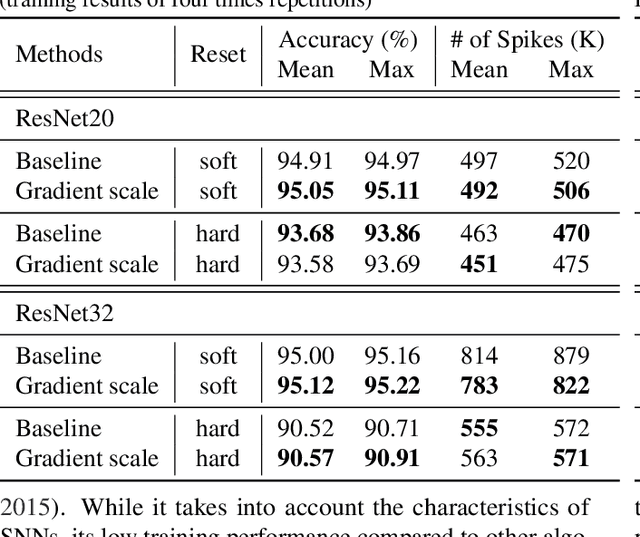
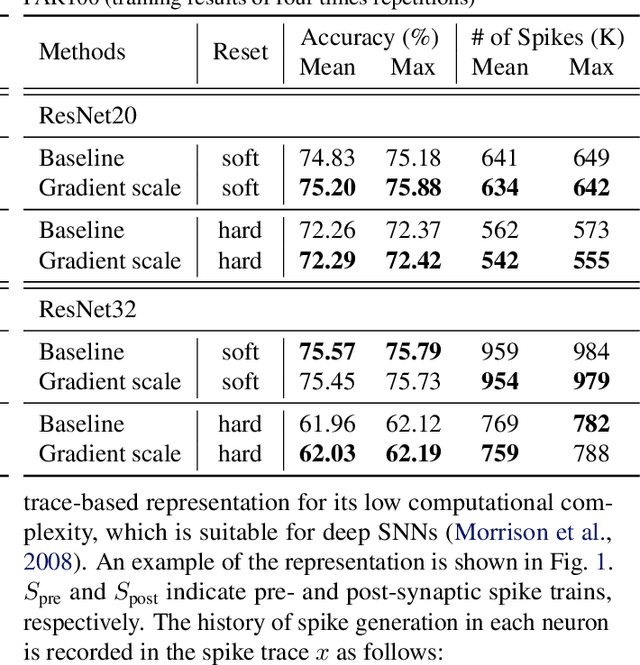
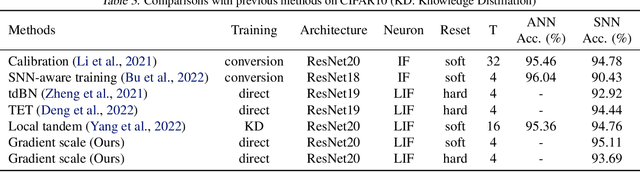
Deep spiking neural networks (SNNs) are promising neural networks for their model capacity from deep neural network architecture and energy efficiency from SNNs' operations. To train deep SNNs, recently, spatio-temporal backpropagation (STBP) with surrogate gradient was proposed. Although deep SNNs have been successfully trained with STBP, they cannot fully utilize spike information. In this work, we proposed gradient scaling with local spike information, which is the relation between pre- and post-synaptic spikes. Considering the causality between spikes, we could enhance the training performance of deep SNNs. According to our experiments, we could achieve higher accuracy with lower spikes by adopting the gradient scaling on image classification tasks, such as CIFAR10 and CIFAR100.

Deep neural network Grad-Shafranov solver constrained with measured magnetic signals

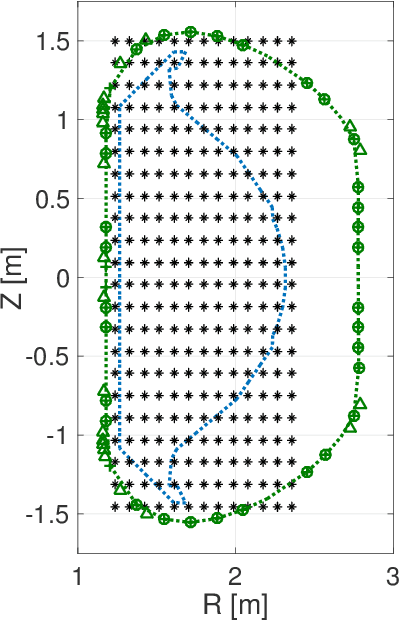
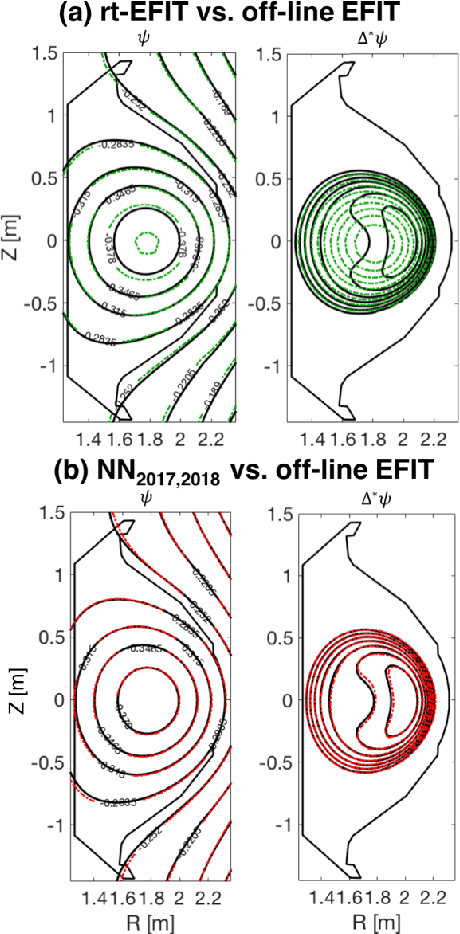
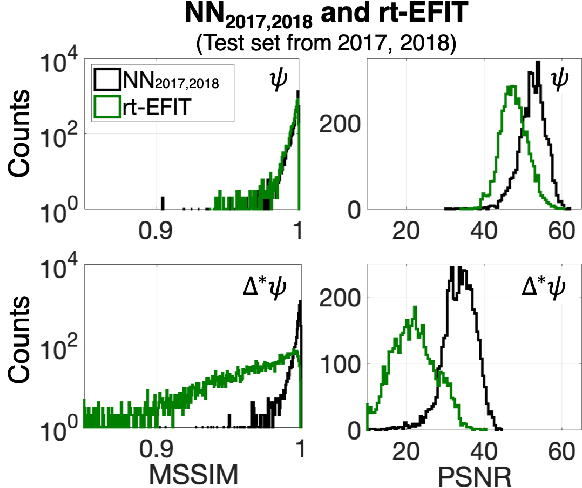
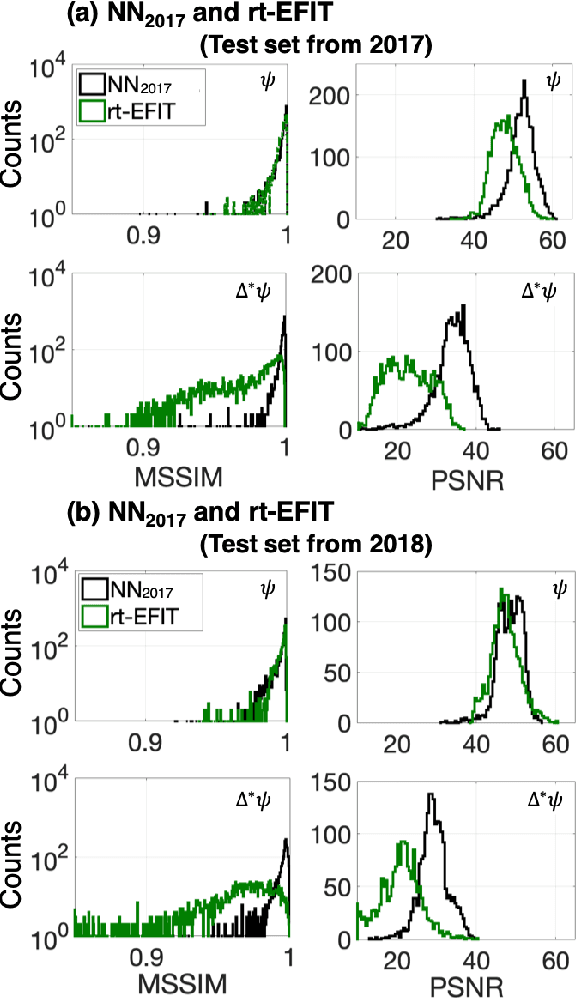
A neural network solving Grad-Shafranov equation constrained with measured magnetic signals to reconstruct magnetic equilibria in real time is developed. Database created to optimize the neural network's free parameters contain off-line EFIT results as the output of the network from $1,118$ KSTAR experimental discharges of two different campaigns. Input data to the network constitute magnetic signals measured by a Rogowski coil (plasma current), magnetic pick-up coils (normal and tangential components of magnetic fields) and flux loops (poloidal magnetic fluxes). The developed neural networks fully reconstruct not only the poloidal flux function $\psi\left( R, Z\right)$ but also the toroidal current density function $j_\phi\left( R, Z\right)$ with the off-line EFIT quality. To preserve robustness of the networks against a few missing input data, an imputation scheme is utilized to eliminate the required additional training sets with large number of possible combinations of the missing inputs.

Markov chain Hebbian learning algorithm with ternary synaptic units

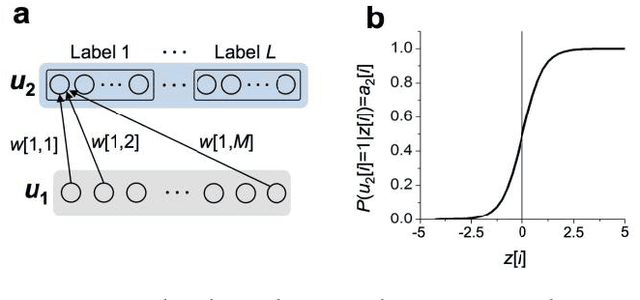
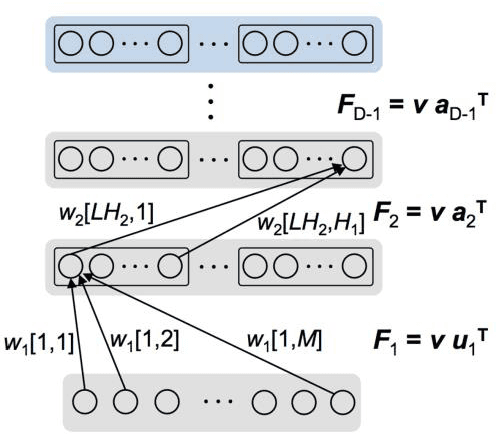
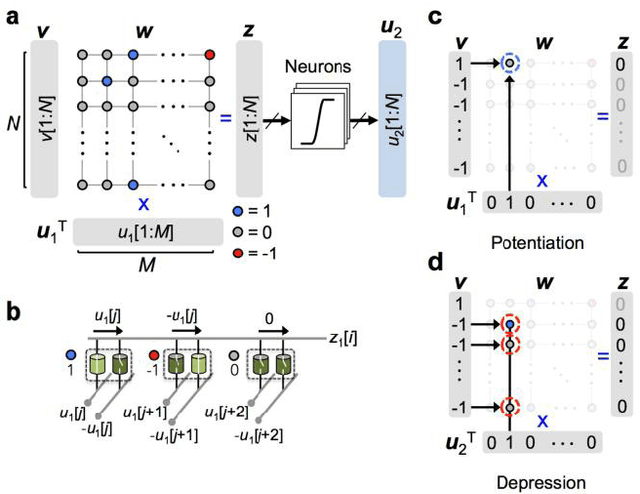
In spite of remarkable progress in machine learning techniques, the state-of-the-art machine learning algorithms often keep machines from real-time learning (online learning) due in part to computational complexity in parameter optimization. As an alternative, a learning algorithm to train a memory in real time is proposed, which is named as the Markov chain Hebbian learning algorithm. The algorithm pursues efficient memory use during training in that (i) the weight matrix has ternary elements (-1, 0, 1) and (ii) each update follows a Markov chain--the upcoming update does not need past weight memory. The algorithm was verified by two proof-of-concept tasks (handwritten digit recognition and multiplication table memorization) in which numbers were taken as symbols. Particularly, the latter bases multiplication arithmetic on memory, which may be analogous to humans' mental arithmetic. The memory-based multiplication arithmetic feasibly offers the basis of factorization, supporting novel insight into the arithmetic.