Simplified calcium signaling cascade for synaptic plasticity

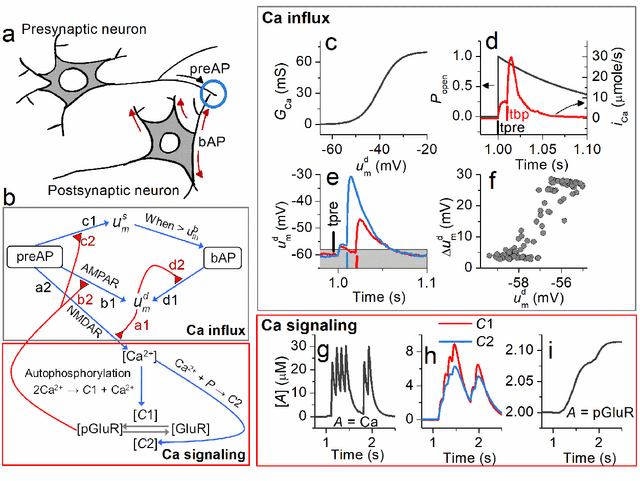
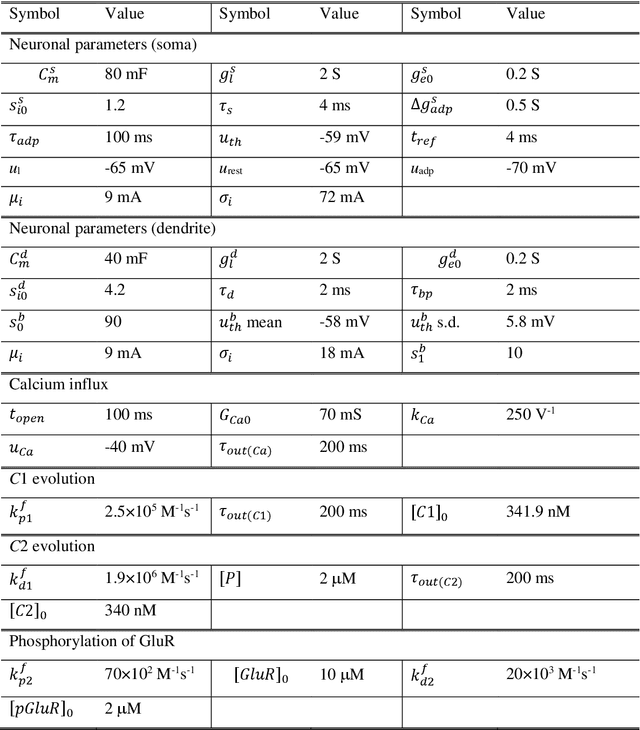
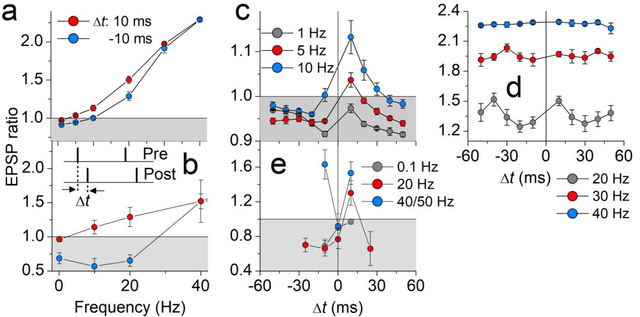
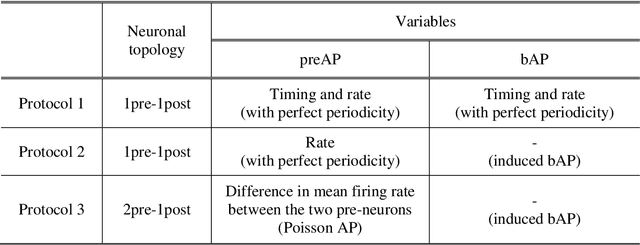
We propose a model for synaptic plasticity based on a calcium signaling cascade. The model simplifies the full signaling pathways from a calcium influx to the phosphorylation (potentiation) and dephosphorylation (depression) of glutamate receptors that are gated by fictive C1 and C2 catalysts, respectively. This model is based on tangible chemical reactions, including fictive catalysts, for long-term plasticity rather than the conceptual theories commonplace in various models, such as preset thresholds of calcium concentration. Our simplified model successfully reproduced the experimental synaptic plasticity induced by different protocols such as (i) a synchronous pairing protocol and (ii) correlated presynaptic and postsynaptic action potentials (APs). Further, the ocular dominance plasticity (or the experimental verification of the celebrated Bienenstock--Cooper--Munro theory) was reproduced by two model synapses that compete by means of back-propagating APs (bAPs). The key to this competition is synapse-specific bAPs with reference to bAP-boosting on the physiological grounds.

Markov chain Hebbian learning algorithm with ternary synaptic units

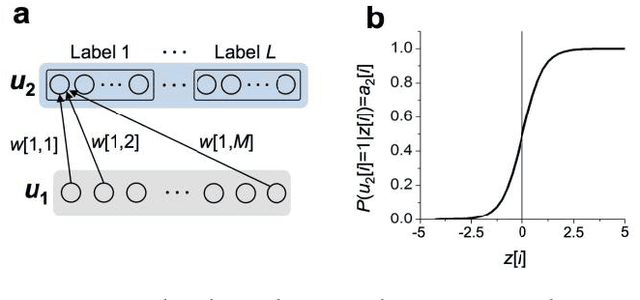
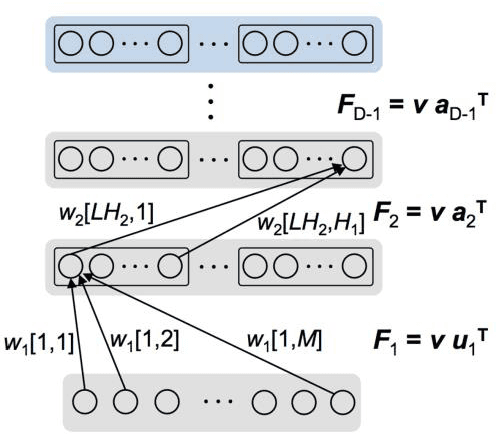
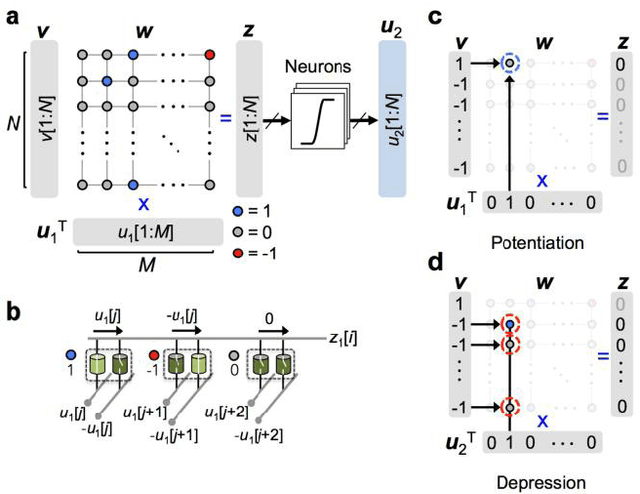
In spite of remarkable progress in machine learning techniques, the state-of-the-art machine learning algorithms often keep machines from real-time learning (online learning) due in part to computational complexity in parameter optimization. As an alternative, a learning algorithm to train a memory in real time is proposed, which is named as the Markov chain Hebbian learning algorithm. The algorithm pursues efficient memory use during training in that (i) the weight matrix has ternary elements (-1, 0, 1) and (ii) each update follows a Markov chain--the upcoming update does not need past weight memory. The algorithm was verified by two proof-of-concept tasks (handwritten digit recognition and multiplication table memorization) in which numbers were taken as symbols. Particularly, the latter bases multiplication arithmetic on memory, which may be analogous to humans' mental arithmetic. The memory-based multiplication arithmetic feasibly offers the basis of factorization, supporting novel insight into the arithmetic.