GraphLab: A New Framework For Parallel Machine Learning

Designing and implementing efficient, provably correct parallel machine learning (ML) algorithms is challenging. Existing high-level parallel abstractions like MapReduce are insufficiently expressive while low-level tools like MPI and Pthreads leave ML experts repeatedly solving the same design challenges. By targeting common patterns in ML, we developed GraphLab, which improves upon abstractions like MapReduce by compactly expressing asynchronous iterative algorithms with sparse computational dependencies while ensuring data consistency and achieving a high degree of parallel performance. We demonstrate the expressiveness of the GraphLab framework by designing and implementing parallel versions of belief propagation, Gibbs sampling, Co-EM, Lasso and Compressed Sensing. We show that using GraphLab we can achieve excellent parallel performance on large scale real-world problems.

Distributed GraphLab: A Framework for Machine Learning in the Cloud

While high-level data parallel frameworks, like MapReduce, simplify the design and implementation of large-scale data processing systems, they do not naturally or efficiently support many important data mining and machine learning algorithms and can lead to inefficient learning systems. To help fill this critical void, we introduced the GraphLab abstraction which naturally expresses asynchronous, dynamic, graph-parallel computation while ensuring data consistency and achieving a high degree of parallel performance in the shared-memory setting. In this paper, we extend the GraphLab framework to the substantially more challenging distributed setting while preserving strong data consistency guarantees. We develop graph based extensions to pipelined locking and data versioning to reduce network congestion and mitigate the effect of network latency. We also introduce fault tolerance to the GraphLab abstraction using the classic Chandy-Lamport snapshot algorithm and demonstrate how it can be easily implemented by exploiting the GraphLab abstraction itself. Finally, we evaluate our distributed implementation of the GraphLab abstraction on a large Amazon EC2 deployment and show 1-2 orders of magnitude performance gains over Hadoop-based implementations.

Efficient Multicore Collaborative Filtering

This paper describes the solution method taken by LeBuSiShu team for track1 in ACM KDD CUP 2011 contest (resulting in the 5th place). We identified two main challenges: the unique item taxonomy characteristics as well as the large data set size.To handle the item taxonomy, we present a novel method called Matrix Factorization Item Taxonomy Regularization (MFITR). MFITR obtained the 2nd best prediction result out of more then ten implemented algorithms. For rapidly computing multiple solutions of various algorithms, we have implemented an open source parallel collaborative filtering library on top of the GraphLab machine learning framework. We report some preliminary performance results obtained using the BlackLight supercomputer.

GraphLab: A Distributed Framework for Machine Learning in the Cloud

Machine Learning (ML) techniques are indispensable in a wide range of fields. Unfortunately, the exponential increase of dataset sizes are rapidly extending the runtime of sequential algorithms and threatening to slow future progress in ML. With the promise of affordable large-scale parallel computing, Cloud systems offer a viable platform to resolve the computational challenges in ML. However, designing and implementing efficient, provably correct distributed ML algorithms is often prohibitively challenging. To enable ML researchers to easily and efficiently use parallel systems, we introduced the GraphLab abstraction which is designed to represent the computational patterns in ML algorithms while permitting efficient parallel and distributed implementations. In this paper we provide a formal description of the GraphLab parallel abstraction and present an efficient distributed implementation. We conduct a comprehensive evaluation of GraphLab on three state-of-the-art ML algorithms using real large-scale data and a 64 node EC2 cluster of 512 processors. We find that GraphLab achieves orders of magnitude performance gains over Hadoop while performing comparably or superior to hand-tuned MPI implementations.

Kernel Belief Propagation

We propose a nonparametric generalization of belief propagation, Kernel Belief Propagation (KBP), for pairwise Markov random fields. Messages are represented as functions in a reproducing kernel Hilbert space (RKHS), and message updates are simple linear operations in the RKHS. KBP makes none of the assumptions commonly required in classical BP algorithms: the variables need not arise from a finite domain or a Gaussian distribution, nor must their relations take any particular parametric form. Rather, the relations between variables are represented implicitly, and are learned nonparametrically from training data. KBP has the advantage that it may be used on any domain where kernels are defined (Rd, strings, groups), even where explicit parametric models are not known, or closed form expressions for the BP updates do not exist. The computational cost of message updates in KBP is polynomial in the training data size. We also propose a constant time approximate message update procedure by representing messages using a small number of basis functions. In experiments, we apply KBP to image denoising, depth prediction from still images, and protein configuration prediction: KBP is faster than competing classical and nonparametric approaches (by orders of magnitude, in some cases), while providing significantly more accurate results.

Parallel Coordinate Descent for L1-Regularized Loss Minimization

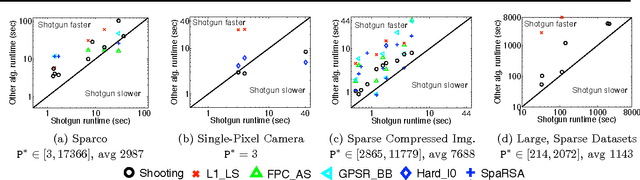
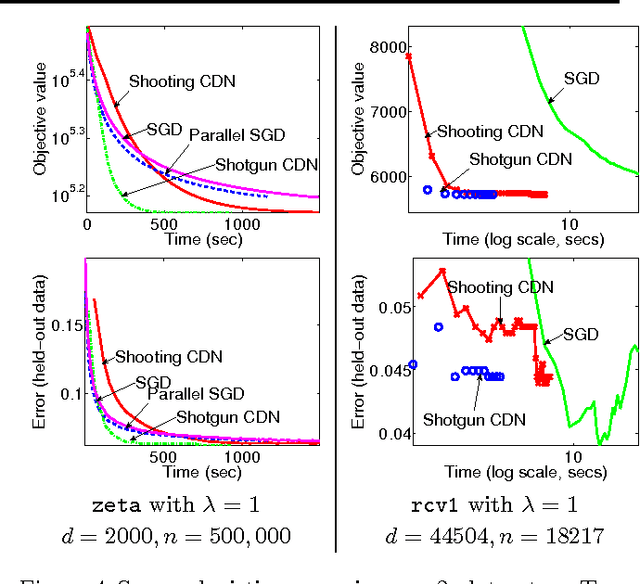
We propose Shotgun, a parallel coordinate descent algorithm for minimizing L1-regularized losses. Though coordinate descent seems inherently sequential, we prove convergence bounds for Shotgun which predict linear speedups, up to a problem-dependent limit. We present a comprehensive empirical study of Shotgun for Lasso and sparse logistic regression. Our theoretical predictions on the potential for parallelism closely match behavior on real data. Shotgun outperforms other published solvers on a range of large problems, proving to be one of the most scalable algorithms for L1.

Inference with Multivariate Heavy-Tails in Linear Models

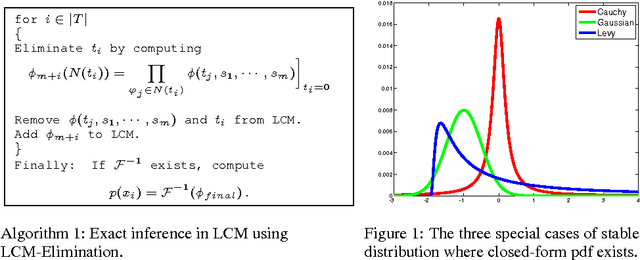
Heavy-tailed distributions naturally occur in many real life problems. Unfortunately, it is typically not possible to compute inference in closed-form in graphical models which involve such heavy-tailed distributions. In this work, we propose a novel simple linear graphical model for independent latent random variables, called linear characteristic model (LCM), defined in the characteristic function domain. Using stable distributions, a heavy-tailed family of distributions which is a generalization of Cauchy, L\'evy and Gaussian distributions, we show for the first time, how to compute both exact and approximate inference in such a linear multivariate graphical model. LCMs are not limited to stable distributions, in fact LCMs are always defined for any random variables (discrete, continuous or a mixture of both). We provide a realistic problem from the field of computer networks to demonstrate the applicability of our construction. Other potential application is iterative decoding of linear channels with non-Gaussian noise.

Fixing Convergence of Gaussian Belief Propagation

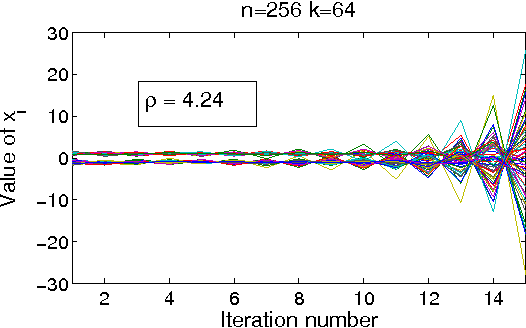
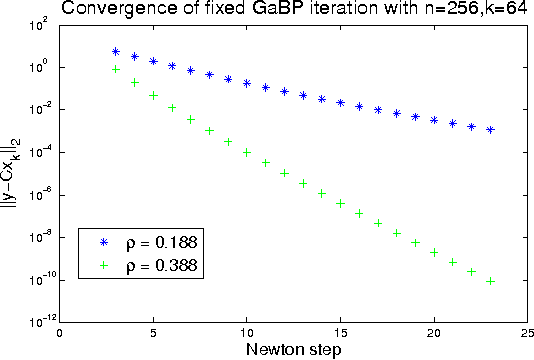
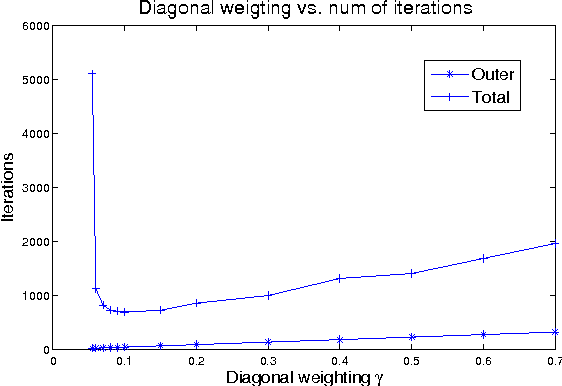
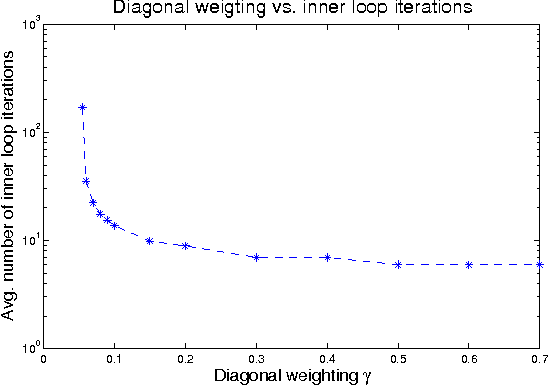
Gaussian belief propagation (GaBP) is an iterative message-passing algorithm for inference in Gaussian graphical models. It is known that when GaBP converges it converges to the correct MAP estimate of the Gaussian random vector and simple sufficient conditions for its convergence have been established. In this paper we develop a double-loop algorithm for forcing convergence of GaBP. Our method computes the correct MAP estimate even in cases where standard GaBP would not have converged. We further extend this construction to compute least-squares solutions of over-constrained linear systems. We believe that our construction has numerous applications, since the GaBP algorithm is linked to solution of linear systems of equations, which is a fundamental problem in computer science and engineering. As a case study, we discuss the linear detection problem. We show that using our new construction, we are able to force convergence of Montanari's linear detection algorithm, in cases where it would originally fail. As a consequence, we are able to increase significantly the number of users that can transmit concurrently.

A Gaussian Belief Propagation Solver for Large Scale Support Vector Machines

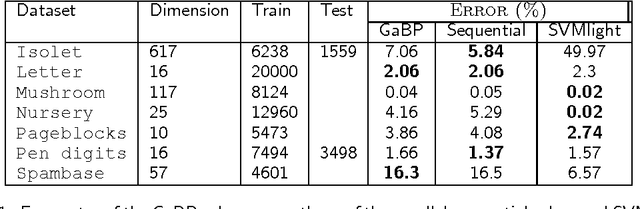
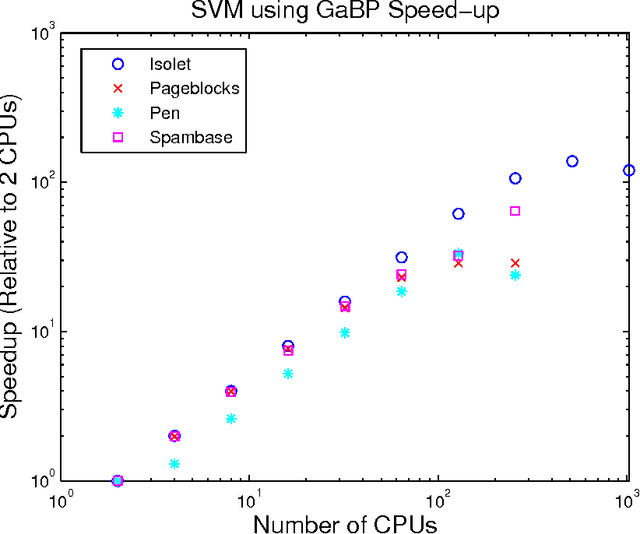
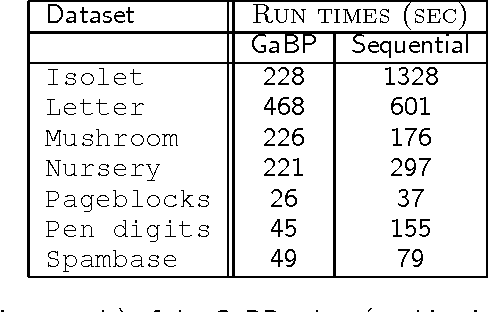
Support vector machines (SVMs) are an extremely successful type of classification and regression algorithms. Building an SVM entails solving a constrained convex quadratic programming problem, which is quadratic in the number of training samples. We introduce an efficient parallel implementation of an support vector regression solver, based on the Gaussian Belief Propagation algorithm (GaBP). In this paper, we demonstrate that methods from the complex system domain could be utilized for performing efficient distributed computation. We compare the proposed algorithm to previously proposed distributed and single-node SVM solvers. Our comparison shows that the proposed algorithm is just as accurate as these solvers, while being significantly faster, especially for large datasets. We demonstrate scalability of the proposed algorithm to up to 1,024 computing nodes and hundreds of thousands of data points using an IBM Blue Gene supercomputer. As far as we know, our work is the largest parallel implementation of belief propagation ever done, demonstrating the applicability of this algorithm for large scale distributed computing systems.