Danny Dolev
Fixing Convergence of Gaussian Belief Propagation
Jul 04, 2009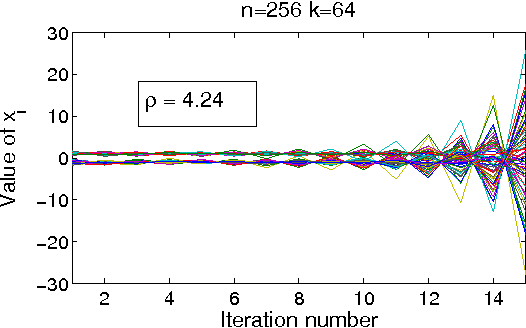
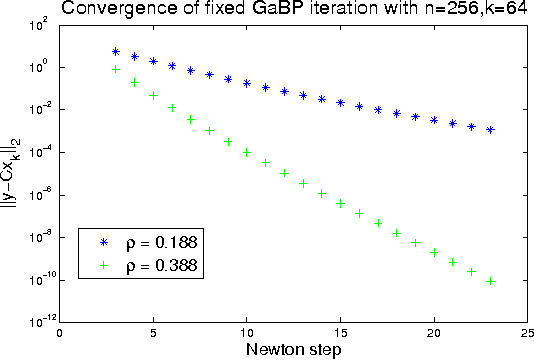
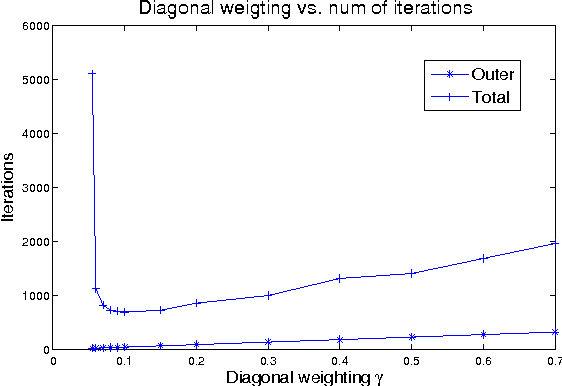
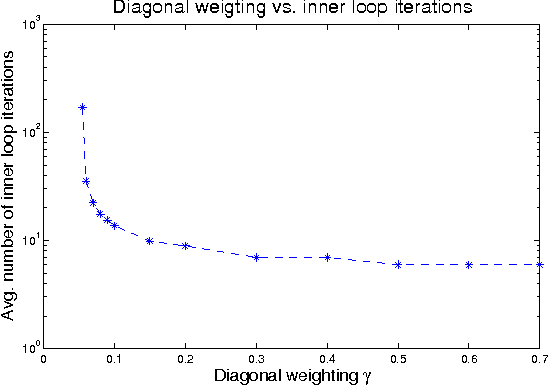
Abstract:Gaussian belief propagation (GaBP) is an iterative message-passing algorithm for inference in Gaussian graphical models. It is known that when GaBP converges it converges to the correct MAP estimate of the Gaussian random vector and simple sufficient conditions for its convergence have been established. In this paper we develop a double-loop algorithm for forcing convergence of GaBP. Our method computes the correct MAP estimate even in cases where standard GaBP would not have converged. We further extend this construction to compute least-squares solutions of over-constrained linear systems. We believe that our construction has numerous applications, since the GaBP algorithm is linked to solution of linear systems of equations, which is a fundamental problem in computer science and engineering. As a case study, we discuss the linear detection problem. We show that using our new construction, we are able to force convergence of Montanari's linear detection algorithm, in cases where it would originally fail. As a consequence, we are able to increase significantly the number of users that can transmit concurrently.
A Gaussian Belief Propagation Solver for Large Scale Support Vector Machines
Oct 09, 2008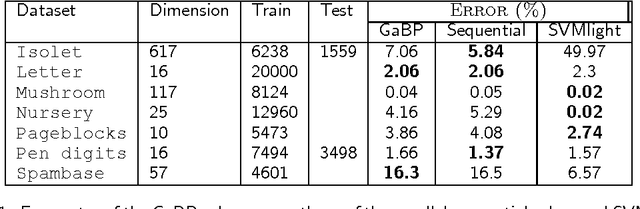
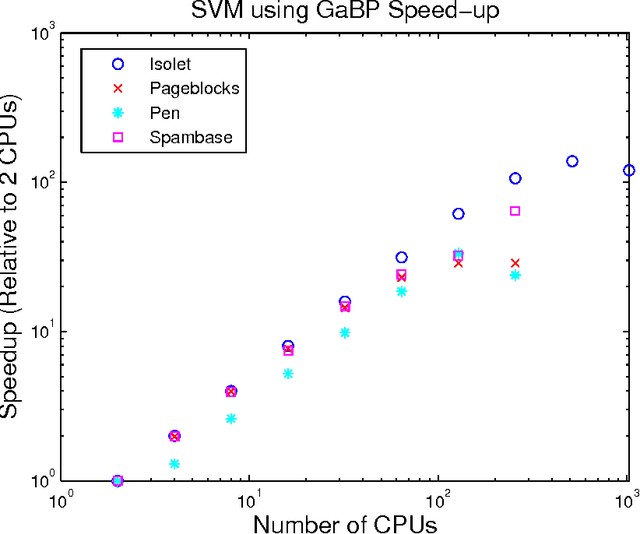
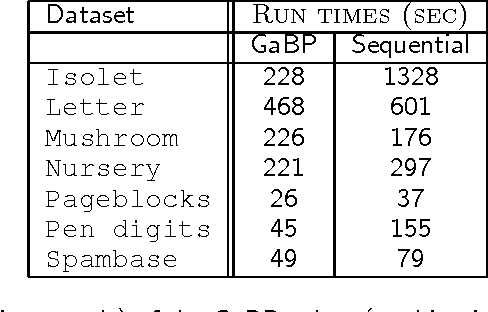

Abstract:Support vector machines (SVMs) are an extremely successful type of classification and regression algorithms. Building an SVM entails solving a constrained convex quadratic programming problem, which is quadratic in the number of training samples. We introduce an efficient parallel implementation of an support vector regression solver, based on the Gaussian Belief Propagation algorithm (GaBP). In this paper, we demonstrate that methods from the complex system domain could be utilized for performing efficient distributed computation. We compare the proposed algorithm to previously proposed distributed and single-node SVM solvers. Our comparison shows that the proposed algorithm is just as accurate as these solvers, while being significantly faster, especially for large datasets. We demonstrate scalability of the proposed algorithm to up to 1,024 computing nodes and hundreds of thousands of data points using an IBM Blue Gene supercomputer. As far as we know, our work is the largest parallel implementation of belief propagation ever done, demonstrating the applicability of this algorithm for large scale distributed computing systems.
* 12 pages, 1 figure, appeared in the 5th European Complex Systems Conference, Jerusalem, Sept. 2008
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge