Carlos E. Guestrin
GraphLab: A New Framework For Parallel Machine Learning
Aug 09, 2014



Abstract:Designing and implementing efficient, provably correct parallel machine learning (ML) algorithms is challenging. Existing high-level parallel abstractions like MapReduce are insufficiently expressive while low-level tools like MPI and Pthreads leave ML experts repeatedly solving the same design challenges. By targeting common patterns in ML, we developed GraphLab, which improves upon abstractions like MapReduce by compactly expressing asynchronous iterative algorithms with sparse computational dependencies while ensuring data consistency and achieving a high degree of parallel performance. We demonstrate the expressiveness of the GraphLab framework by designing and implementing parallel versions of belief propagation, Gibbs sampling, Co-EM, Lasso and Compressed Sensing. We show that using GraphLab we can achieve excellent parallel performance on large scale real-world problems.
Robust Combination of Local Controllers
Jan 10, 2013



Abstract:Planning problems are hard, motion planning, for example, isPSPACE-hard. Such problems are even more difficult in the presence of uncertainty. Although, Markov Decision Processes (MDPs) provide a formal framework for such problems, finding solutions to high dimensional continuous MDPs is usually difficult, especially when the actions and time measurements are continuous. Fortunately, problem-specific knowledge allows us to design controllers that are good locally, though having no global guarantees. We propose a method of nonparametrically combining local controllers to obtain globally good solutions. We apply this formulation to two types of problems : motion planning (stochastic shortest path) and discounted MDPs. For motion planning, we argue that usual MDP optimality criterion (expected cost) may not be practically relevant. Wepropose an alternative: finding the minimum cost path,subject to the constraint that the robot must reach the goal withhigh probability. For this problem, we prove that a polynomial number of samples is sufficient to obtain a high probability path. For discounted MDPs, we propose a formulation that explicitly deals with model uncertainty, i.e., the problem introduced when transition probabilities are not known exactly. We formulate the problem as a robust linear program which directly incorporates this type of uncertainty.
Distributed Planning in Hierarchical Factored MDPs
Dec 12, 2012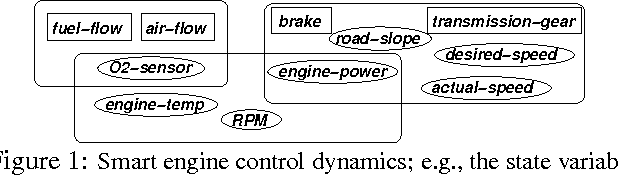


Abstract:We present a principled and efficient planning algorithm for collaborative multiagent dynamical systems. All computation, during both the planning and the execution phases, is distributed among the agents; each agent only needs to model and plan for a small part of the system. Each of these local subsystems is small, but once they are combined they can represent an exponentially larger problem. The subsystems are connected through a subsystem hierarchy. Coordination and communication between the agents is not imposed, but derived directly from the structure of this hierarchy. A globally consistent plan is achieved by a message passing algorithm, where messages correspond to natural local reward functions and are computed by local linear programs; another message passing algorithm allows us to execute the resulting policy. When two portions of the hierarchy share the same structure, our algorithm can reuse plans and messages to speed up computation.
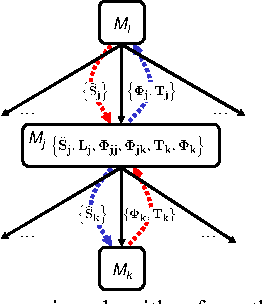
Robust Probabilistic Inference in Distributed Systems
Jul 11, 2012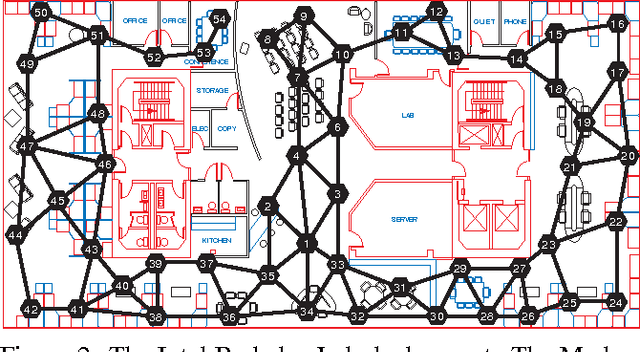
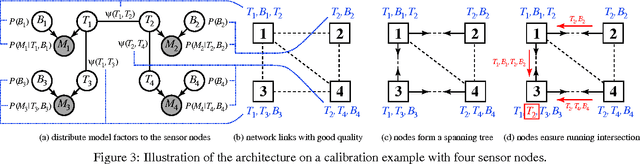
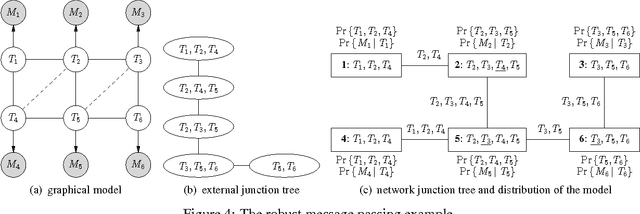
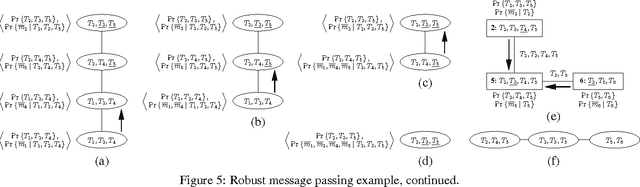
Abstract:Probabilistic inference problems arise naturally in distributed systems such as sensor networks and teams of mobile robots. Inference algorithms that use message passing are a natural fit for distributed systems, but they must be robust to the failure situations that arise in real-world settings, such as unreliable communication and node failures. Unfortunately, the popular sum-product algorithm can yield very poor estimates in these settings because the nodes' beliefs before convergence can be arbitrarily different from the correct posteriors. In this paper, we present a new message passing algorithm for probabilistic inference which provides several crucial guarantees that the standard sum-product algorithm does not. Not only does it converge to the correct posteriors, but it is also guaranteed to yield a principled approximation at any point before convergence. In addition, the computational complexity of the message passing updates depends only upon the model, and is dependent of the network topology of the distributed system. We demonstrate the approach with detailed experimental results on a distributed sensor calibration task using data from an actual sensor network deployment.
Solving Factored MDPs with Continuous and Discrete Variables
Jul 11, 2012



Abstract:Although many real-world stochastic planning problems are more naturally formulated by hybrid models with both discrete and continuous variables, current state-of-the-art methods cannot adequately address these problems. We present the first framework that can exploit problem structure for modeling and solving hybrid problems efficiently. We formulate these problems as hybrid Markov decision processes (MDPs with continuous and discrete state and action variables), which we assume can be represented in a factored way using a hybrid dynamic Bayesian network (hybrid DBN). This formulation also allows us to apply our methods to collaborative multiagent settings. We present a new linear program approximation method that exploits the structure of the hybrid MDP and lets us compute approximate value functions more efficiently. In particular, we describe a new factored discretization of continuous variables that avoids the exponential blow-up of traditional approaches. We provide theoretical bounds on the quality of such an approximation and on its scale-up potential. We support our theoretical arguments with experiments on a set of control problems with up to 28-dimensional continuous state space and 22-dimensional action space.
Near-optimal Nonmyopic Value of Information in Graphical Models
Jul 04, 2012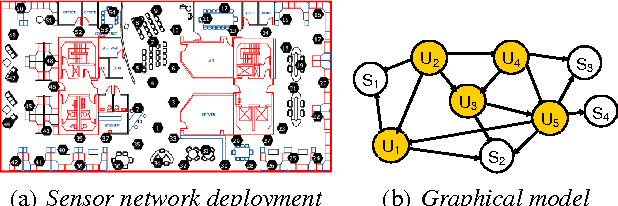

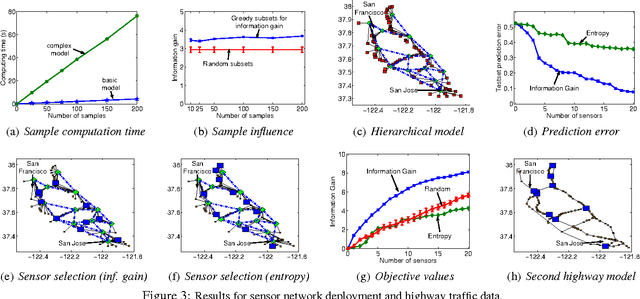
Abstract:A fundamental issue in real-world systems, such as sensor networks, is the selection of observations which most effectively reduce uncertainty. More specifically, we address the long standing problem of nonmyopically selecting the most informative subset of variables in a graphical model. We present the first efficient randomized algorithm providing a constant factor (1-1/e-epsilon) approximation guarantee for any epsilon > 0 with high confidence. The algorithm leverages the theory of submodular functions, in combination with a polynomial bound on sample complexity. We furthermore prove that no polynomial time algorithm can provide a constant factor approximation better than (1 - 1/e) unless P = NP. Finally, we provide extensive evidence of the effectiveness of our method on two complex real-world datasets.
Distributed Parallel Inference on Large Factor Graphs
May 09, 2012



Abstract:As computer clusters become more common and the size of the problems encountered in the field of AI grows, there is an increasing demand for efficient parallel inference algorithms. We consider the problem of parallel inference on large factor graphs in the distributed memory setting of computer clusters. We develop a new efficient parallel inference algorithm, DBRSplash, which incorporates over-segmented graph partitioning, belief residual scheduling, and uniform work Splash operations. We empirically evaluate the DBRSplash algorithm on a 120 processor cluster and demonstrate linear to super-linear performance gains on large factor graph models.
Efficient Probabilistic Inference with Partial Ranking Queries
Feb 14, 2012

Abstract:Distributions over rankings are used to model data in various settings such as preference analysis and political elections. The factorial size of the space of rankings, however, typically forces one to make structural assumptions, such as smoothness, sparsity, or probabilistic independence about these underlying distributions. We approach the modeling problem from the computational principle that one should make structural assumptions which allow for efficient calculation of typical probabilistic queries. For ranking models, "typical" queries predominantly take the form of partial ranking queries (e.g., given a user's top-k favorite movies, what are his preferences over remaining movies?). In this paper, we argue that riffled independence factorizations proposed in recent literature [7, 8] are a natural structural assumption for ranking distributions, allowing for particularly efficient processing of partial ranking queries.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge