Distributed Planning in Hierarchical Factored MDPs
Paper and Code
Dec 12, 2012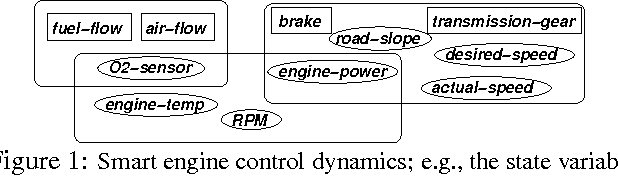

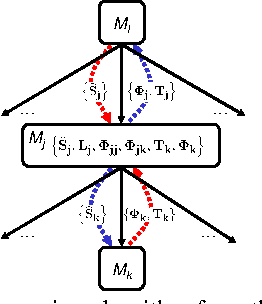

We present a principled and efficient planning algorithm for collaborative multiagent dynamical systems. All computation, during both the planning and the execution phases, is distributed among the agents; each agent only needs to model and plan for a small part of the system. Each of these local subsystems is small, but once they are combined they can represent an exponentially larger problem. The subsystems are connected through a subsystem hierarchy. Coordination and communication between the agents is not imposed, but derived directly from the structure of this hierarchy. A globally consistent plan is achieved by a message passing algorithm, where messages correspond to natural local reward functions and are computed by local linear programs; another message passing algorithm allows us to execute the resulting policy. When two portions of the hierarchy share the same structure, our algorithm can reuse plans and messages to speed up computation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge