Near-optimal Nonmyopic Value of Information in Graphical Models
Paper and Code
Jul 04, 2012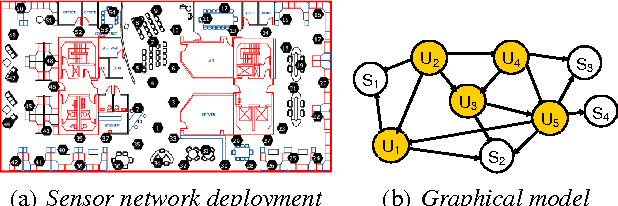

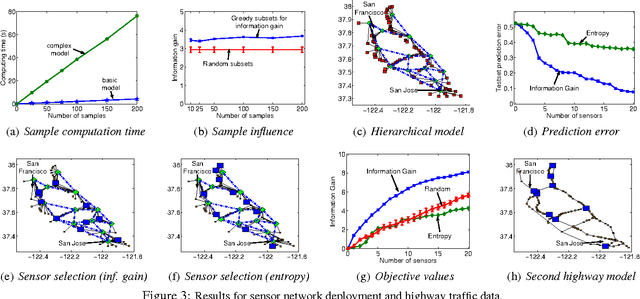
A fundamental issue in real-world systems, such as sensor networks, is the selection of observations which most effectively reduce uncertainty. More specifically, we address the long standing problem of nonmyopically selecting the most informative subset of variables in a graphical model. We present the first efficient randomized algorithm providing a constant factor (1-1/e-epsilon) approximation guarantee for any epsilon > 0 with high confidence. The algorithm leverages the theory of submodular functions, in combination with a polynomial bound on sample complexity. We furthermore prove that no polynomial time algorithm can provide a constant factor approximation better than (1 - 1/e) unless P = NP. Finally, we provide extensive evidence of the effectiveness of our method on two complex real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge